AC Circuit Containing R and L Numerical Class-12 Nootan ISC Physics Solution Ch-12 Alternating Current. Step by step solutions of Kumar and Mittal Physics of Nageen Prakashan as council latest prescribe guideline for upcoming exam. Visit official Website CISCE for detail information about ISC Board Class-12 Physics.
AC Circuit Containing R and L Numerical Class-12 Nootan ISC Physics Solution Ch-12 Alternating Current
| Board | ISC |
| Class | 12 |
| Subject | Physics |
| Book | Nootan |
| Chapter-12 | Alternating Current. |
| Topics | Numericals on AC Circuit Containing R and L |
| Academic Session | 2025-2026 |
Numericals on AC Circuit Containing R and L
Class-12 Nootan ISC Physics Solution Ch-12 Alternating Current
Que-15: A 100 V-50 Hz AC source is connected to a series combination of an inductance of 100 mH and a resistance of 25 Ω. Calculate the magnitude and phase of current.
Ans- It is an L-R circuit
XL = 2πfL = 2 x 3.14 x 50 x 100 x 10^-3 = 31.4 Ω
again Z = √(XL²+R²) = √(31.4²+25²) = 40 Ω
∴ i = V/Z = 100/40 = 2.5 A
Que-16: The inductance and resistance of a choke-coil are 0.2 H and 0.5 Ω respectively. A current of 2.0 A (rms) and frequency 50 Hz is passed through it. What will be the PD across its ends?
Ans- XL = 2πfL = 2 x 3.14 x 50 x 0.2 = 62.8 Ω
∴ Z = √(XL²+R²) = √(62.8²+5²) = 63 Ω
∴ v = iZ = 2 x 63 = 126 volt
Que-17: A non-inductive resistance of 12 Ω and an inductance of 0.05 H of negligible resistance are connected in series in an AC circuit having frequency 50 Hz and voltage 130 V. Determine impedance and current in the circuit.
Ans- XL = 2πfL = 2 x 3.14 x 50 x 0.05 = 15.7 Ω
again Z = √(XL²+R²) = √(15.7²+12²) = 19.76 Ω
∴ i = V/Z = 130/19.76 = 6.58 A
Que-18: A current of 2.0 A is flowing in the given L-R circuit. Find the voltage across the AC source and the impedance of the circuit.
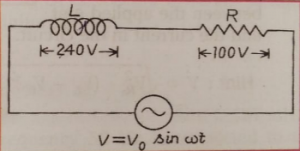
Ans- V = √(VL²+VR²) = √(240²+100²) = 260 V
Impedance Z = V/i = 260/2 = 130 Ω
Que-19: An alternating emf of 110 V is applied to a circuit containing a resistance of 40 Ω and an inductance L in series. The current lags behind the emf by an angle tan^-1 (3/4). Find the inductive reactance, impedance of the circuit and current in the circuit. If L = 0.1 H, find the frequency of applied emf.
Ans- tan φ = 3/4 = XL/R = XL/40
=> XL = 30 Ω
Z = √(XL²+R²) = √(30²+40²) = 50 Ω
∴ i = V/Z = 110/50 = 2.2 A
ω = XL/L = 30/0.1 = 300 rad/s
Que-20: A bulb of resistance 10 Ω, connected to an inductor of inductance L, is in series with an AC source marked 100 V, 50 Hz. If the phase angle between the voltage and the current is pi / 4 radian, find the value of L.
Ans- tan φ = tan π/4 = XL/R = XL/10 = 1
=> XL = 10 Ω
again XL = 2πfL
=> L = XL/2πf
=> 10/ 2 x π x 50 = 1/10π H
Que-21: For the given circuit, find (i) the reactance, (ii) the impedance, (iii) the peak value of current and (iv) the phase difference between voltage and current. (tan^-1(1.33) = 53 deg)
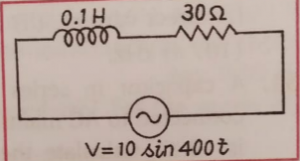
Ans-

Que-22: An AC circuit has a resistance and an inductance connected in series, as shown. Calculate the current and the power factor in the circuit.
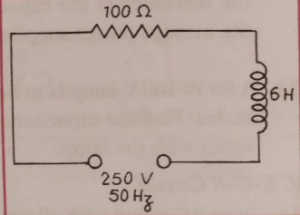
Ans- XL = 2πfL = 2 x 3.14 x 50 x 6 = 1884 Ω
now Z = √(XL²+R²) = √(1884²+100²) = 1887 Ω
now i = 250/1887 = 0.1325 A
Power factor = R/Z = 100/1884 = 0.053
Que-23: A current of 1.1 A flows through a coil when connected to a 110 V DC source. When 110 V-50 Hz AC is applied to the same coil, only 0.5 A current flows. Calculate the resistance, impedance and inductance of the coil.
Ans-
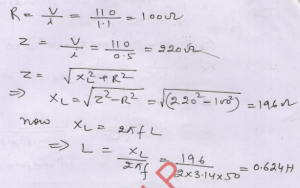
Que-24: An AC circuit consists of a 220 V, 50 Hz supply connected across a 100 Ω resistor. What inductance should be introduced in the circuit in series with the resistance so that the current is reduced to half?
Ans- i = 220/100 = 2.2 A
for half current (1.1 A)
Z = 220/1.1 = 200 Ω
now XL² = Z² -R²
=> XL² = 200²-100²= 100 x 300
=> XL = 173 Ω
∴L = XL/2πf = 173/(2 x 3.14 x 50) = 0.55 H
Que-25: A coil has a current of 1.0 A and a power of 100 W from an AC source of 110 V and 50 Hz. Find the resistance and the inductance of the coil.
Ans-
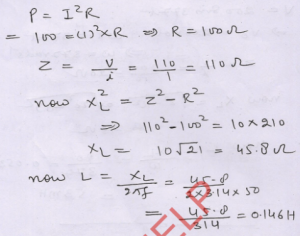
Que-26: An emf V = 200sin 377 t volt is applied across an inductance L having a resistance of 1.0 Ω. The maximum current is found to be 10 A. Find the value of L.
Ans- V = 200 sin 377 t
=> Vo = 200 volt
ωt = 377 t => ω = 377 rad/s
Z = V/i = 200/10 = 20 Ω
now XL² = Z² -R²
=> XL² = 20²-1²
=> XL = 20 Ω
now L = XL/ω = 20/377 = 0.053 = 53 mH
Que-27: An electric lamp which runs at 80 V DC, consumes 10 A current. The lamp is connected to 100V-50 Hz AC source. Compute the inductance of the choke required.
Ans- VL² = V² -VR²
=> VL² = 100² -80²
=> VL = 60
XL = VL/i = 60/10 = 6Ω
now L = XL/2πf = 6 / 2 x 3.14 x 50
=> 6/314 = 0.02 H
— : End of AC Circuit Containing R and L Numerical Class-12 Nootan ISC Physics Solution Ch-12 :–
Return to : – Nootan Solutions for ISC Class-12 Physics
Thanks
Please share with your friends


