Angles and Arc Lengths Class 11 OP Malhotra Exe-3A ISC Maths Solutions Ch-3 Solutions. In this article you would learn about Magnitude, Measures of angles and Area of Circle Sector. Step by step solutions of latest textbook has been given as latest syllabus. Visit official Website CISCE for detail information about ISC Board Class-11 Mathematics.

Angles and Arc Lengths Class 11 OP Malhotra Exe-3A ISC Maths Solutions Ch-3
| Board | ISC |
| Publications | S Chand |
| Subject | Maths |
| Class | 11th |
| Chapter-3 | Angles and Arc Lengths |
| Writer | OP Malhotra |
| Exe-3(A) | Magnitude, Measures of angles and Area of Circle Sector. |
Exercise- 3A
Angles and Arc Lengths Class 11 OP Malhotra Exe-3A Solution.
Que-1: Express the following angles in degrees : (π/6), (14π/15), (11π/18), (7π/90)
Sol: We know that π rad = 180°
⇒ 1 rad = 180°/π
∴ (π/6) rad = (180°/π) × (π/6) = 30°
(14π/15) rad = (180°/π) × (14π/15) = 168°
(11π/18) rad = (180°/π) × (11π/18) = 110°
and (7π/90) rad = (180°/π) × (7π/90) = 14°
Que-2: Express the following angles in radians
(i) 1′ (ii) 20° (iii) 135°.
Sol: We know that n radian = 180°
1° = (π/180) rad
(i) 1′ = (1/60)° = (1/60)×(π/180) rad
= π/10800 rad
(ii) 20° = (20)×(π/180) rad
= π/9 rad
(iii) 135° = (135)×(π/180) rad
= 3π/4 rad.
Que-3:Express in radians and also in degrees the angle of a regular polygon of (i) 40 sides, (ii) n sides.
Sol: We know that exterior angle = 360° no. of sides
(i) Here n = 40
∴ exterior angle = 360°/40 = 9° = (π/20) rad [∵ π rad = 180°]
∴ interior angle of polygon = 180° – 9° = 171°
(In radians) interior angle of polygon
= π – (π/20) = 19π/20.
(ii) each exterior angle = 360°/n or 2π/n
∴ each interior angle of polygon with sides
n = 180° – (360°/n) = {(n−2)/n} 180°
or π − (2π/n) = (n−2n)/π radians
Que-4: In a circle of diameter 40 cm, the length of a chord is 20 cm, find the length of minor arc of the chord.
Sol: Given that the diameter of the circle = 40 cm and the length of the chord is 20 cm.
⇒ Radius of the circle = half of diameter = 20 cm.
Let AB be the chord whose length is 20 cm ( given)
By joining the radii to the ends of the chord, we get a triangle AOB.
In triangle AOB, OA = OB = 20 cm (radii of circle)
AB = 20 cm (given the length of the chord)
∴ Triangle AOB is an equilateral triangle with all sides equal.
⇒ Θ = 60° = π / 3 radian.
As we know that, in a circle of radius r unit, if the length of the arc is l unit subtends at an angle Θ radian at the center, then l = r × Θ
⇒ l = 20 × π / 3
⇒ l = 20 π/3 cm.
Que-5: The length of a pendulum is 8 m while the pendulum swings through 1.5 rad, find the length of the arc through which the tip of the pendulum passes.
Sol: Given length of pendulum = r = 8m
Also, angle through pendulum swings θ = 1.5 rad
∴ required length of arc through which tip of the pendulum passes = s = rθ
= (8 x 1.5) m = 12m
Que-6: The minute hand of a clock is 15 cm long. How far does the tip of the hand move during 40 minutes ? (Take π = 3.14)
Sol: given length of minute hand of clock = r = 15 cm
since angle moved by minute hand in 60′ = 360°
∴ angle moved by minute hand in 40′ = (360/60) x 40 = 240°
∴ θ = 240°
We know that n radians = 180°
1° = (π/180) rad
240° = (240)×(π/180) rad
= 4π/3 rad
Also, θ = l/r
l = θr = 15×(4/3)×3.14
= 62.85 cm.
Thus the tip of the minute hand moving during 40 minutes be 62.85 cm.
Que-7: A central angle of a circle of radius 50 cm intercepts an arc of 10 cm. Express the central angle 0 in radians and in degrees.
Sol: Given radius of circle = r = 60 cm
length of arc = l = 10 cm
∴ required central angle of circle
θ = l/r = 10/50 = 1/5 rad
We know that, π radians = 180°
∴ θ = (1/5) rad = (180°/π) × (1/5)
= (180°/22) × (7/5)
= (126°/11) = 11°27′11′′
Que-8: The moon’s distance from the earth is 360000 km and its diameter subtends an angle of 31′ at the eye of the observer. Find the diameter of the moon.
Sol: Here θ = 31′ = (31/60)° [∵ 1° = 60′ ⇒ 1′ = (1/60)°]
Also π rad = 180° ⇒ 1° = (π/180) rad
∴ θ = {(31/60) x (π/180)} rad
Since the distance between the moon and earth is quite large so we consider diameter AB as arc AB
We know that, θ = l/r
⇒ (31/60) × (π/180) = diameter/360000
diameter of moon = (31/60) × (π/180) x 360000
= (31/60) × (22/7×180) x 360000
= 68200/21 km
Que-9: A railway train is travelling on a curve of 750 m radius at the rate of 30 km/h, through what angle has it turned in 10 seconds ?
Sol: Given radius of curve = r = 750 m
given distance travelled by train in 1 hour = 30 km = (30 x 1000) m
∴ distance covered by train in 1 second
= 30000/(60×60)
Thus distance covered by train in 10 seconds
= l = {(30000/3600) x 10)}
Therefore required angle has it turned in 10 seconds = θ = l/r
= (30000×10)/(3600×750)
= 1/9 rad.
Que-10: A horse is tethered to a stake by a rope 810 cm long. If the horse moves along the circumferences of a circle always keeping the rope tight, find how far it will have gone when the rope has traced out an angle of 70° ?
Sol: Let O denote the position of point and OP denote the length of rope in tight position.
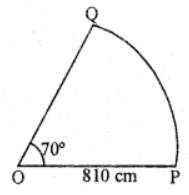
∠POQ = 70°
QP = 810 = r cm
We know that ∠POQ = (arc PQ)/OP
arc PQ = (70°×810)
= {(π/180)×70×810}
= {(22/7)×(1/180)×70×810} cm
= 990 cm.
Que-11: The area of a sector of 6.024 cm² and its angle is 36°. Find the radius, (π = 3.14).
Sol: Let O be the centre of circle with radius r
Then area of sector AOB with central angle θ
= (1/2)r²θ where θ = 30°
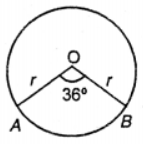
Also, given area of sector = 5.024 cm²
= (1/2)r²θ = 5.024
= (1/2)r² × 36 × (π/180) = 5.024
= (r²π)/10 = 5.024
= r² = 5.024 × 10 × (22/7)
= r² = 15.98545
r = 4 cm.
Que-12: Find the area of sector of a circle, radius 5 m bounded by an arc of length 8 in.
Sol: Given radius of sector of circle = r = 5 m
given arc of length = l = 8 m
∴ Central angle θ = l/r = 8/5 rad
Thus, required area of sector of circle
= (1/2)r²θ = (1/2)×5²×(8/5) = 20 m²
Que-13: The diagram shows a windscreen wiper cleaning a car windscreen.
(i) What is the length of the arc swept out?
(ii) What area of the windscreen is not cleaned?
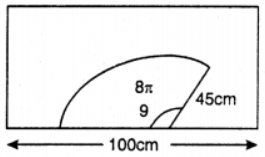
Sol: (i) Given θ = 8π/9
∴ required length of arc swept out = l = rθ
= (4/5) x (8π/9) = 40π = 40 × (22/7) cm
= 126 cm
(ii) area of car windscreen = (55 x 100) cm²
= 5500 cm²
∴ area of windscreen is not cleaned = area of car windscreen – area of windscreen cleaned
= 5500 – (1/2)r² θ
= (5500 – (1/2) x 45 x 45 x (8/9) x (22/7)) cm²
= (5500 – 2828.57) cm²
= 2671.42 cm²
Que-14: Find the area of the shaded segment in given below figure.
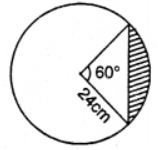
Sol: Area of sector = (1/2)r² θ
= (1/2)×24×24×60°
= 12×24×(π/3) cm²
= 12×24×(22/21)
= 301.7142 cm²
area of ΔAOB = (1/2)×OA×OB×sin60°
= (1/2)×24×25×(√3/2)
= 144√3 = 249.2193 cm²
Required area of shaded region = area of sector AOB – area of ΔAOB
= (301.7142 – 249.2193) cm²
= 52.298 cm².
Que-15: What is the ratio of the areas of the major sector in diagram A to the minor sector in a diagram B?
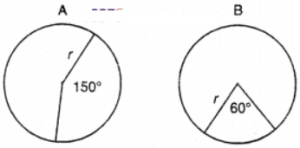
Sol: A1 = area of major sector in diagram A
= (1/2)r² θ = (1/2)r² (150°)
= (1/2)r² (π/180)× 150
= (1/2)r² (5π/6)
A2 = area of minor sector in diagram B
= (1/2)r² (π/3)
Required ratio = A1/A2
= {(1/2)r² (5π/6)} / {(1/2)r² (π/3)}
= (5π/6) × (π/3)
= 5/2
= 5 : 2.
–: End Angles and Arc Lengths Class 11 OP Malhotra Exe-3A ISC Math Ch-3 Solutions :–
Return to :- OP Malhotra ISC Class-11 S Chand Publication Maths Solutions
Thanks
Please share with your friends


