Area of Plane Figures Class 9 OP Malhotra Exe-16D ICSE Maths Solutions

Area of Plane Figures Class 9 OP Malhotra Exe-16D ICSE Maths Solutions Ch-16.  We Provide Step by Step Solutions / Answer of Area of Trapezium for OP Malhotra Maths. Visit official Website CISCE for detail information about ICSE Board Class-9 Mathematics.

Area of Plane Figures Class 9 OP Malhotra Exe-16D ICSE Maths Solutions Ch-16D

Board	ICSE
Publications	S Chand
Subject	Maths
Class	9th
Chapter-16	Area of Plane Figures
Writer	OP Malhotra
Exe-16D	Solved Questions on Area of Trapezium
Edition	2025-2026

Solved Questions on Area of Trapezium

Area of Plane Figures Class 9 OP Malhotra Exe-16D ICSE Maths Solutions Ch-16.

Que-1: Find the area of the trapezium if the :
(i) Parallel sides are 3 cm and 6 cm and perp. distance between them is 10 cm.
(ii) Parallel sides are 25 m and 33 m and perp. distance between them is 20 m.

Sol: (i) Length of parallel sides are
3 cm and 6 cm
and perpendicular distance (h) between them = 10 cm

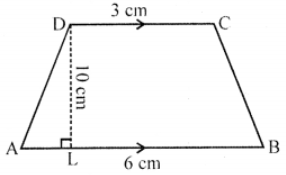
∴ Area = (1/2) (Sum of parallel sides) × height
= (1/2) (6 + 3) × 10
= 9 × 5 = 45 cm²
(ii) Parallel sides are 25 m and 33 m
and perpendicular distance (h) = 20 m
∴ Area = (1/2) (sum of parallel sides × height)
= (1/2) (25 + 33) × 20
= 58 × 10 = 582 m²

Que-2: The area of a trapezium is 240 m² and the sum of the parallel sides is 48 m. Find the height.

Sol: Area of trapezium = 240 m²
Sum of parallel sides = 48 m
Height = (Area × 2) / Sum of parallel sides
H = (240×2)/48
= 10 m

Que-3: The parallel sides of a trapezium are 4.36 cm and 3.18 cm and area is 18.85 cm². Find the distance between the parallel sides.

Sol: Parallel sides of trapezium are 4.36 cm and 3.18 cm
Area = 18.85 cm²
∴ Distance between the parallel sides (h)
Height = (Area × 2) / Sum of parallel sides
H = (18.85×2)/(4.36+3.18)
= (18.85×2)/7.54
= 37.70/7.54
= 5 cm

Que-4: The area of a trapezium is 475 cm² and the height is 19 cm. Find its two parallel sides if one side is 4 cm greater than the other.

Sol: Area of trapezium = 475 cm²
Height (h) = 19 cm
∴ Sum of two parallel sides = (Area × 2) / Height
= (475×2)/19 = 50 cm
Let one of the two parallel sides = x
Then second side = x + 4
∴ x + x + 4 = 50 ⇒ 2x = 50 – 4 = 46
x = 46/2 = 23
∴ First side = 23 cm
and second side = 23 + 4 = 27 cm

Que-5: The parallel sides of a trapezium are in the ratio 2 : 5 and the distance between the parallel sides is 10 cm. If the area of the trapezium is 350 cm², find the lengths of its parallel sides.

Sol: Ratio in parallel sides = 2 : 5
Distance between them (h) = 10 cm
and area = 350 cm²
∴ Sum of parallel sides = (Area × 2) / Height
= (350×2)/10 = 70 cm
Sum of ratio = 2 + 5 = 7
∴ First side = (70×2)/7 = 20 cm
and second side = (70×5)/7 = 50 cm

Que-6: In the figure, AD = BC = 5 cm, AB = 7 cm. The parallel sides AB, DC are 4 cm apart. DC = x cm. Find x and the area of the trapezium ABCD.

Sol: In the figure, ABCD is a trapezium in which
AD = BC = 5 cm
AB = 7 cm, DC = x cm
and distance between the parallel sides = 4 cm

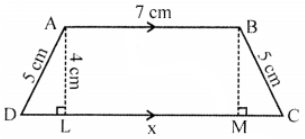
Draw AL and BM ⊥s on DC
AL = BM = 4 cm
AB = LM = 4 cm
∵ AD = BC = 7 cm
∴ ABCD is an isosceles trapezium
Now in right △ALD
AD² = AL² + LD² (Pythagoras Theorem)
(5)² = (4)² + LD²
⇒ 25 = 16 + LD²
LD² = 25 – 16 = 9 = (3)²
∴ x = LD = 3 cm
∴ DC = AB + 2 LD
= 7 + 2 × 3 = 7 + 6 = 13 cm
Now area of trapezium = (1/2)(sum of parallel sides) × height
= (1/2) (7 + 13) × 4
= (1/2) × 20 × 4 = 40 cm²
∴ x = 13 and area = 40 cm²

Que-7: The parallel sides of a trapezium are 7.5 cm, 3.9 cm, and the other sides are each 2.6 cm. Find its area.

Sol: In trapezium ABCD
AB = 7.5 cm, CD = 3.9 cm
AD = BC = 2.6 cm

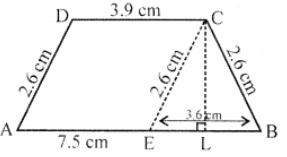
Draw CE || DA, CL ⊥ AB
∴ CE = 2.6 cm and AE = DC = 3.9 cm
∴ EB = AB – AE = 7.5 – 3.9 = 3.6 cm
In an isosceles △CEB, CL ⊥ EB
Which bisects EB at L
∴ EL = (1/2) EB = (1/2) × 3.6 = 1.8 cm
Now in right △CEL
CE² = CL² + EL² (Pythagoras Theorem)
⇒ (2.6)² = CL² + (1.8)²
⇒ 6.76 = CL² + 3.24
⇒ CL² = 6.76 – 3.24 = 3.52
∴ CL = √3.52 = 1.876
Now area of trapezium = (1/2) (sum of parallel sides) × height
= (1/2) (7.5+3.9) × 1.876
= (1/2) × 11.4 × 1.186 = 5.7 × 1.876 cm²
=10.6932 cm²
= 10.7 cm²

Que-8: The given figure shows that cross section of a concrete structure with the measurements, as given. Calculate the area of the cross section.

Sol: In the figure, produce DE to meet AB at G Now we have one trapezium GBCD and one rectangle AGEF

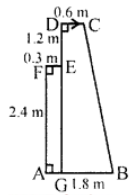
Now GB = AB – AG = AB – FE = 1.8 – 0.3 = 1.5 cm
and DG = DE + EG = DE + FA = 1.2 + 2.4 = 3.6 cm
Now area of rectangle AGEF = l × b = 2.4 × 0.3 = 0.72 cm²
and area of trapezium GBCD = (1/2) (sum of parallel sides) × height
= (1/2) (GB + DC) × DG
= (1/2) (1.5 + 0.6) × 3.6 cm²
= (1/2) × 2.1 × 3.6 = 2.1 × 1.8 cm²
= 3.78 cm²
Area of the whole figure = 0.72 + 3.78
= 4.50 cm² = 4.5 cm²

Que-9: In the figure, find (i) AB (ii) Area of the trapezium ABCD.

Sol: (i) In the figure, draw CE || AB meeting AD in E, then
AE = BC = 2 and DE = AD – EA
= 8 – 2 = 6 cm

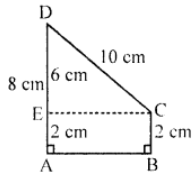
In right △ECD
CD² = D² + EC² (Pythagoras Theorem)
(10)² = (6)² + E²
100 = 36 + E²
⇒ EC² = 100 – 36 = 64 = (8)²
∴ EC = 8 cm or AB = EC = 8 cm
(ii) Now area of trapezium ABCD
= (1/2) (sum of parallel sides) × height
= (1/2) (AD + BC) × AB
= (1/2) (8 + 2) × 8
= (1/2) × 10 × 8 cm² = 40 cm²

Que-10: The cross-section of a tunnel perpendicular to its length is a trapezium ABCD as shown in the figure. AM = BN ; AB = 4.4 m; CD = 3 m. The height of the tunnel is 2.4 m. The tunnel is 50 m long. Calculate :
(i) the cost of painting the internal surface of the tunnel (excluding the floor) at the rate of Rs. 5 per m².
(ii) the cost of paving the floor at the rate of Rs. 18 per m².

Sol: In the figure, ABCD is a trapezium in which AM = BN, AB = 4.4 m, CD = 3 m and height of the tunnel = 2.4 m
Length of tunnel = 50 m
∵ DM and CN are perpendiculars on AB and
AM = NB = (1/2) (AB – DC)
= (1/2) (4.4 – 3.0) m
= (1/2) (1.4) = 0.7 m
In right △ADM,
AD² = DM² + AM² = (2.4)² + (0.7)²
= 5.76 + 0.49 = 6.25 = (2.5)²
∴ AD = CB = 2.5 m

(i) Now area of the interval surface of the tunnel (excluding floor) = Perimeter of the face × Length
= (3 + 2.5 + 2.5) × 50 m²
= 8 × 50 = 400 m²
Rate of painting = Rs. 5 per m²
Total cost = Rs. 400 × 5 = Rs. 2000

(ii) Area of floor = 4.4 × 50 = 220 m²
Rate of paving = Rs. 18 per m²
∴ Total cost of paving the floor = Rs. 18 × 220 = Rs. 3960

Que-11: A trapezium with its parallel sides in the ratio 11 : 3 is cut off from a rectangle whose sides measure 98 cm and 12 cm. The area of the trapezium is (3/7)  of the area of the rectangle. Find the lengths of the parallel sides of the trapezium, when its height is equal to the smaller side of the rectangle.

Sol: Sides of rectangle are 98 cm and 12 cm
∴ Area = l × b = 98 × 12 cm² = 1176 cm²
∴ Area of trapezium = (3/7) of 1176 = 504 cm²
Height of trapezium (h) = smaller side of rectangle = 12 cm
∴ Sum of parallel sides = (Area × 2) / Height = (504×2)/12 cm
= 42 × 2 = 84 cm
Ratio of the parallel sides = 11 : 3
Sum of ratios = 11 + 3 = 14
∴ First side = (84×11)/14 = 66 cm
and second side = (84×3)/14 = 18 cm

Que-12: The cross-section of a canal is in the shape of a trapezium. If the canal is 12 m wide at the top and 8 m wide at the bottom and the area of its cross-section is 84 m², determine its depth.

Sol: Area of cross-section = 84 m²
Sides are 12 m and 8 m

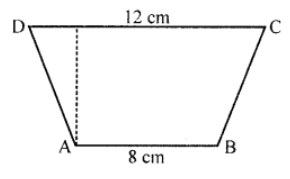
Let h be its depth, then
h = (Area × 2) / Sum of parallel sides
= (84×2)/(12+8) = (84×2)/20
= 168/20 m = 84 m
∴ Depth of the canal = 8.4 m

–; End of Area of Plane Figures Class 9 OP Malhotra Exe-16D ICSE Maths Ch-16 Solutions / Answer :–

Return to :–  OP Malhotra S Chand Solutions for ICSE Class-9 Maths

Thanks

Please Share with Your Friends