Arithmetic Mean, Median, Mode and Quartiles Class 10 OP Malhotra Exe-18A ICSE Maths Solutions Ch-18 Questions as latest prescribe guideline for upcoming exam. In this article you would learn How to Find Mean of Grouped and Ungrouped Data. Visit official Website CISCE for detail information about ICSE Board Class-10 Mathematics.

Arithmetic Mean Class 10 OP Malhotra Exe-18A ICSE Maths Solutions Ch-18
| Board | ICSE |
| Publications | S Chand |
| Subject | Maths |
| Class | 10th |
| Chapter-18 | Arithmetic Mean, Median, Mode and Quartiles |
| Writer | OP Malhotra |
| Exe-18A | How to Find Arithmetic Mean |
| Edition | 2024-2025 |
How to Find Arithmetic Mean
- Direct Method
- Assumed Mean Method
- Step-deviation Method.
Arithmetic Mean of Ungroup Data, = Sum of all Observations / Total Number of Observations
Arithmetic Mean of Grouped Data: ∑ FX / ∑ F
Exercise- 18A ( Arithmetic Mean )
Arithmetic Mean, Median, Mode and Quartiles Class 10 OP Malhotra Exe-18A ICSE Maths Solutions Ch-18
Que-1: Find the number half-way between 0.2 and 0.02.
Sol: Half-way number (average) between 0.2 and 0.02
= (0.2+0.02)/2
= 0.22/2 = 0.11
Que-2: Find the mean of the following sets of numbers :
(a) 4, 5, 7, 8
(b) 3, 5, 0, 2, 8
(c) 2.5, 2.4, 3.5, 2.8, 2.9, 3.3, 3.6
(d) -6, -2, -1, 0, 1, 2, 5, 9
(e) First five prime numbers
(f) First eight even natural numbers
(g) All factors of 30
(h) First five multiples of 8
(i) x, x+1, x+2, x+3, x+4, x+5, x+6
Sol: (a) 4, 5, 7, 8
Here n = 4
∴ Mean = Sum n = (4+5+7+8)/4 = 24/4 = 6
(b) 3, 5, 0, 2, 8
Here n = 5
∴ Mean = (3+5+0+2+8)/5 = 18/5 = 3.6
(c) 2.5, 2.4, 3.5, 2.8, 2.9, 3.3, 3.6
Here n = 8
∴ Mean = (2.5+2.4+3.5+2.8+2.9+3.3+3.6)/7 = 21.0/7 = 3.0
(d) -6,-2,-1,0, 1,2, 5, 9
Here n = 8
∴ Mean = (−6−2−1+0+1+2+5+9)/8 = (−9+17)/8 = 8/8 = 1
(e) First 5 prime numbers are 2, 3, 5,7, 11
∴ Mean = (2+3+5+7+11)/5 = 28/5 = 5.6
(f) First 8 even natural numbers are 2, 4, 6, 8, 10, 12, 14, 16
∴ Mean = (2+4+6+8+10+12+14+16)/8 = 72/8 = 9
(g) All factors of 30 are 1, 2. 3, 5, 6, 10, 15, 30
Here n = 8
∴ Mean = (1+2+3+5+6+10+15+30)/8 = 72/8 = 9
(h) First 5 multiples of 8 are 8, 16, 24, 32, 40
∴ Mean = (8+16+24+32+40)/5 = 120/5 = 24
(i) x, x + 1, x + 2, x + 3, x + 4, x + 5, x + 6
Here n = 7
Mean = (x+x+1+x+2+x+3+x+4+x+5+x+6)/7 = (7x+21)/7 = {7(x+3)}/7 = x + 3
Que-3: The mean of the numbers 6, y, 7, x, 14 is 8. Express y in terms of x.
Sol: 6, y, 7, x, 14
Here n = 5 and Mean = 8
Total sum = nx¯ = 5 × 8 = 40
∴ 6 + y + 7 + x + 14 = 40
⇒ 7 + x + 27 = 40
⇒ 7 = 40 – 27 – x
= 13 – x
Que-4: Nisha secured 73, 86, 78 and 75 marks in four tests. What is the least number of points she should secure in her next test if she has to have an average of 80?
Sol: Number of total tests = 5
Average of 5 tests = 80
∴ Total points, Nisha secured = 5 × 80 = 400
But her score in 4 tests = 73 + 86 + 78 + 75 = 312
∴ Score in fifth test = 400 – 312 = 88
Que-5: A class of 10 students was given a test in Mathematics. The marks, out of 50, secured by the students were as follows :
31, 36, 27, 38, 45, 39, 32, 29, 41, 38 Find the mean score.
Sol: Here n = 10
and scores are 31, 36, 27, 38, 45, 39, 32, 29, 41, 38
∴ Sum = 31 + 36 + 27 + 38 + 45 + 39 + 32 + 29+ 41 + 38 = 356
∴ Mean = 356/10 = 35.6
Que-6: Find the mean of the following frequency distributions:
(a)

(b)

(c)

(d)

Sol: (a) Mean = ∑fx/∑f = 1600/50 = 32 kg

(b) Mean = ∑fx/∑f = 11904/0 = 29.75

(c) Mean = ∑fx/∑f = 90/15 = 6
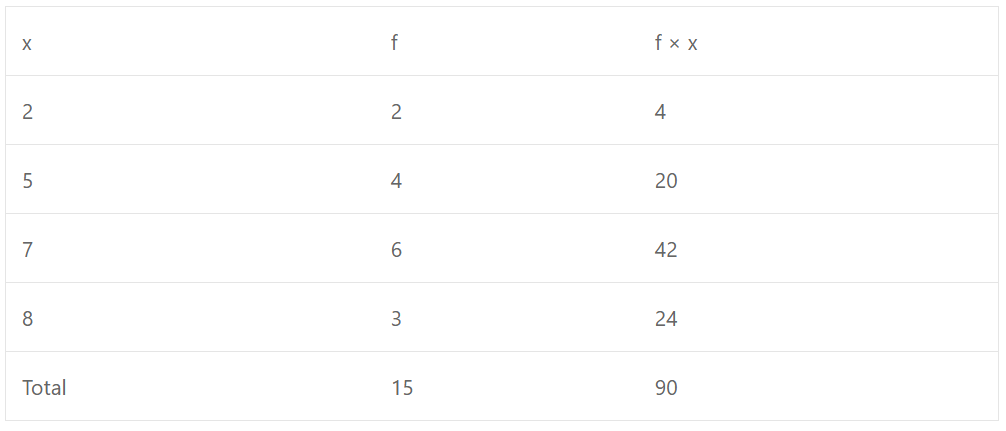
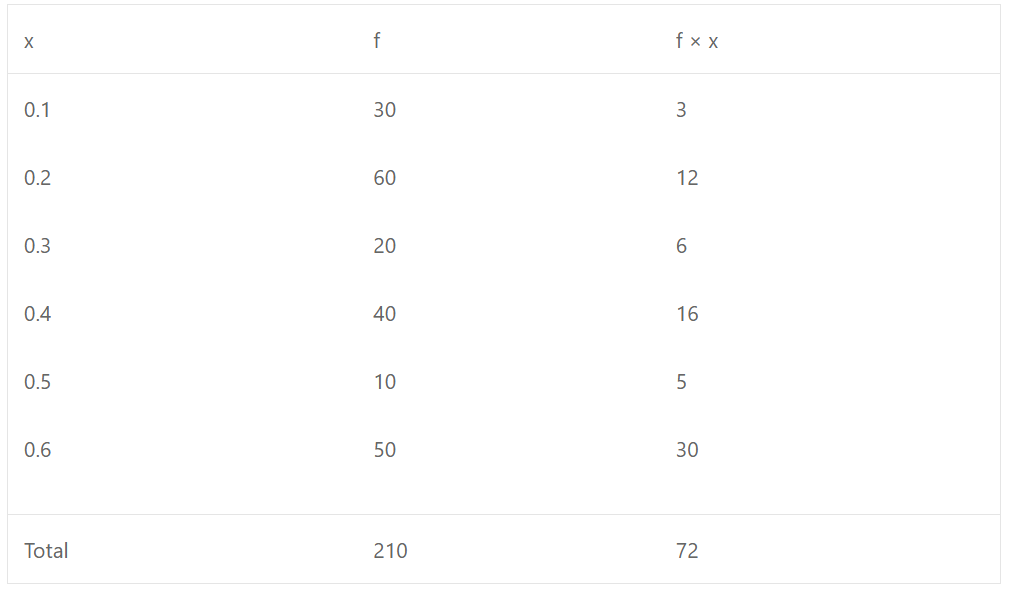
(d) Mean = ∑fx/∑f = 72/210 = 12/35 = 0.34
Que-7: Fill in the blanks : While calculating the mean of the grouped data, we make the assumption that frequency in any class is centred at its
Sol: Mean of grouped data in any class is called its class mark.
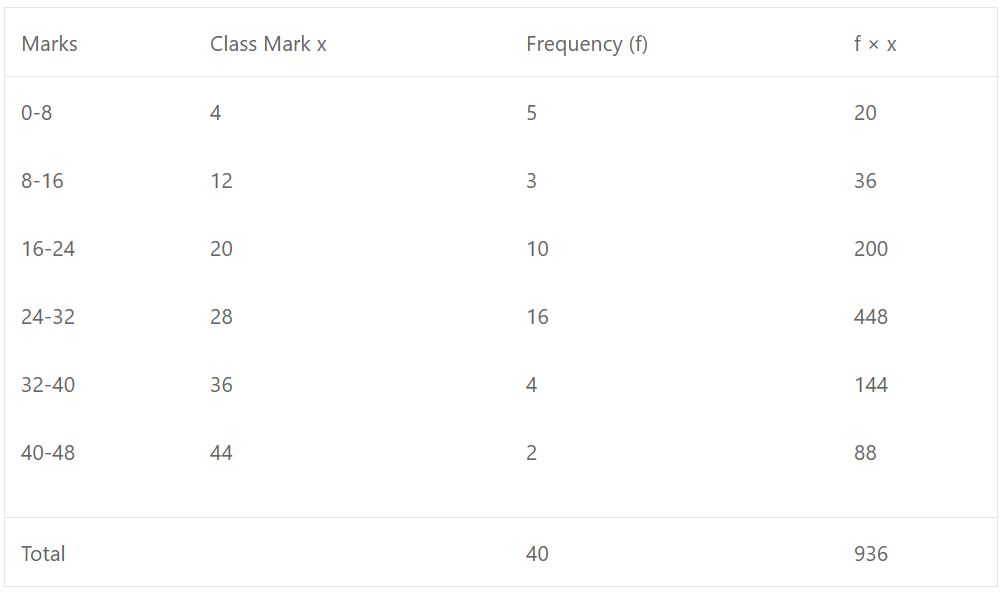
Que-8: The frequency distribution of marks obtained by 40 students of a class is as under : Calculate the Arithmetic mean.

Sol: Mean = ∑fx/∑f = 936/40 = 23.4 marks
Que-9: Find the mean of the following data:
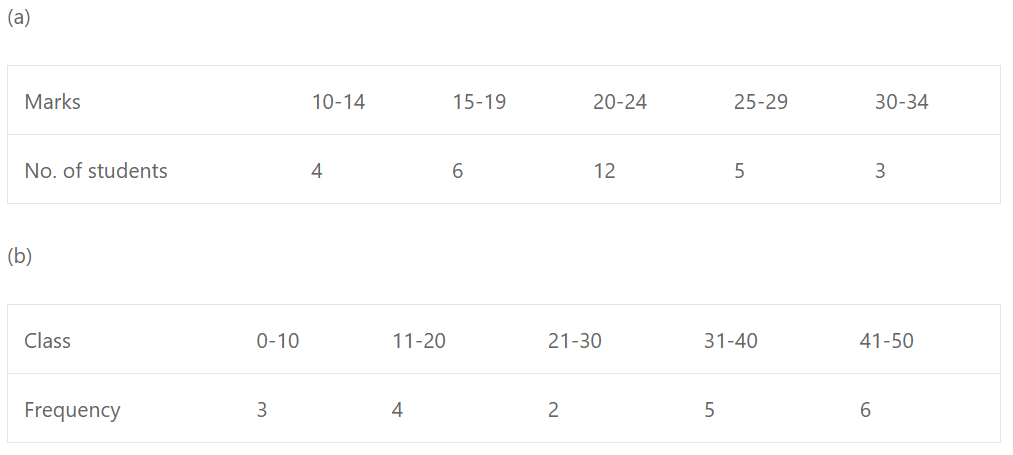
Sol: (a) Mean = ∑fx/∑f = 645/30 = 21.5 marks
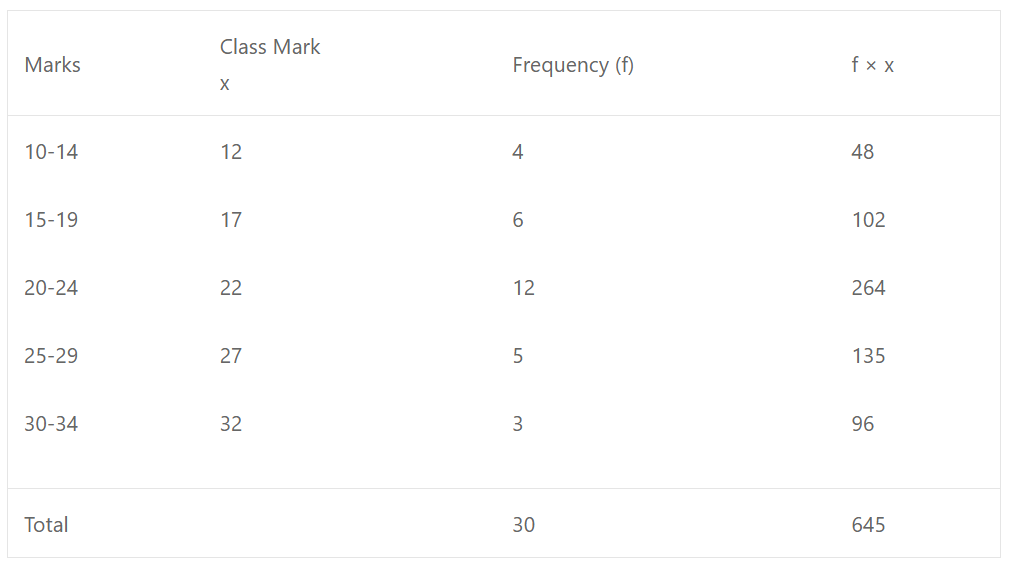
(b) Mean = ∑fx/∑f = 578.5/20 = 28.925
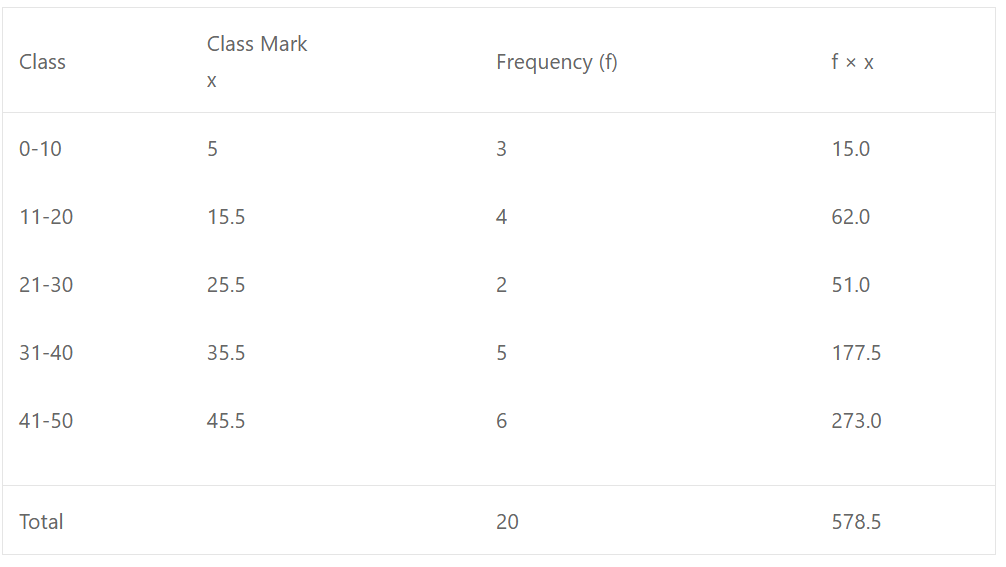
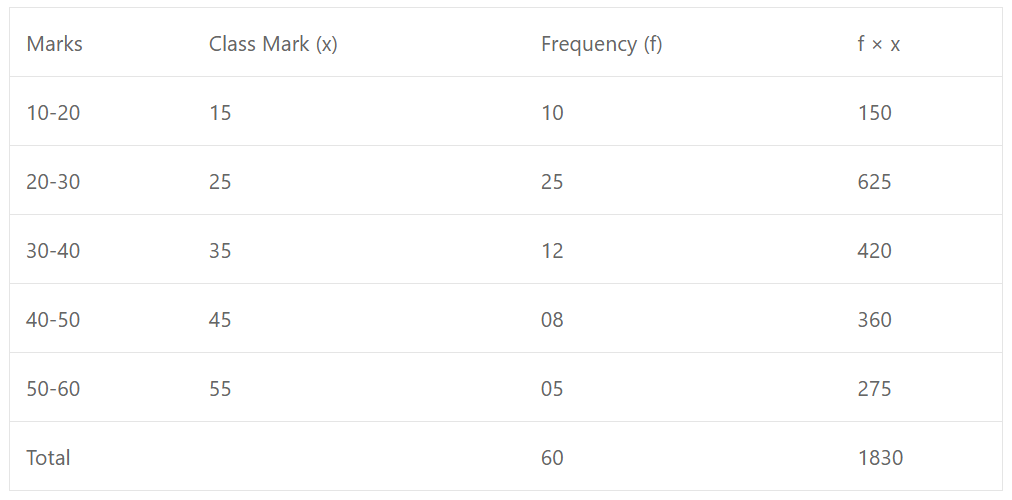
Que-10: In a class of 60 boys the marks obtained in a monthly test were as under : Find the mean marks of the class.
Sol: Mean = ∑fx/∑f = 1830/60 = 30.5
Que-11: Compute the mean of the following frequency table by: (i) direct-method and (ii) short-cut method

Sol: (i) Direct method — Mean = ∑fx/∑f = 1100/50 = 22
(ii) Short-cut method— Mean = A + [∑fd/∑f ] = 27.5 + [−275/50] = 27.5 – 5.5 = 22
![(i) Direct method — Mean = ∑fx/∑f = 1100/50 = 22 (ii) Short-cut method— Mean = A + [∑fd/∑f ] = 27.5 + [−275/50] = 27.5 – 5.5 = 22](https://icsehelp.com/wp-content/uploads/2025/02/11a-1.png)
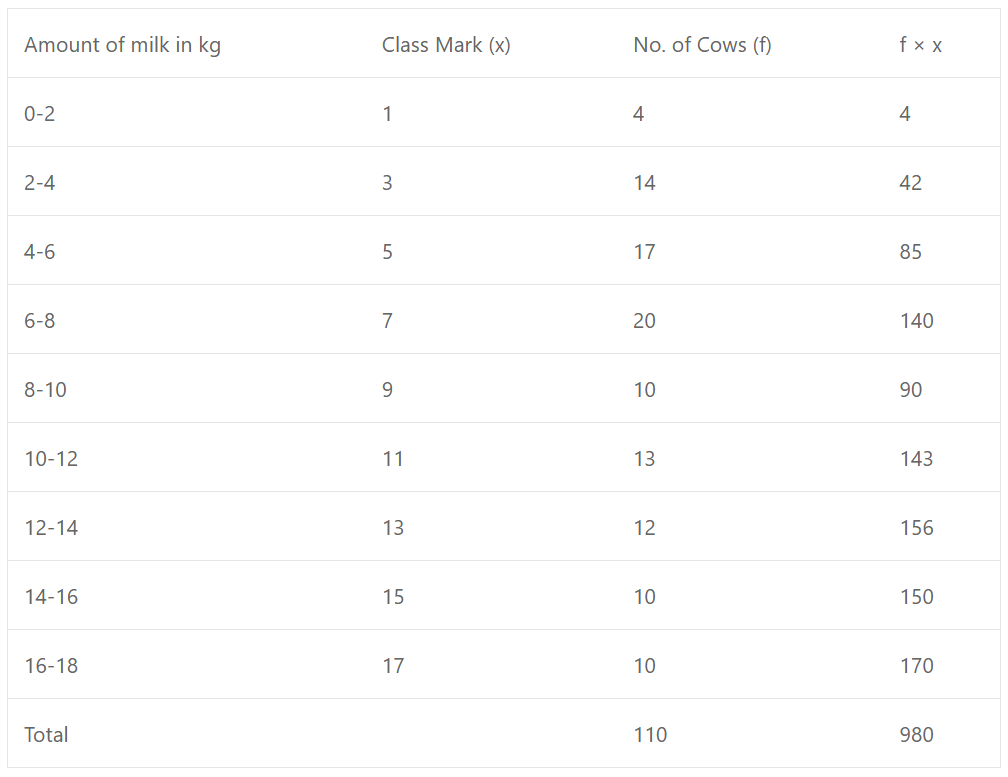
Que-12: The following table gives the classification of 100 cows of a dairy farm, according to the amount of milk given by each in a dairy.

Calculate the mean correct to first place of decimal.
Sol: Mean = ∑fx/∑f = 980/110 = 8.9 kg
Que-13: The weights (in grams) of 50 apples picked out at random from a consignment are given below : 82, 118, 80,110, 104, 84, 106,107, 76, 82,109,107,115, 93,187, 95,123,125, 111, 92, 86, 70,126, 78,130, 129,139,119,115,128,100,186,84, 99, 113,204, 111, 141,136,123, 90, 115, 98, 110, 78, 90, 107, 81, 131, 75.
(i) What is the range of the weights ?
(ii) Form a frequency distribution with class intervals 70-89, 90-109, and so on.
(iii) Use your frequency distribution to calculate the mean.
Sol: (i) Maximum weight = 204 g
Minimum weight = 70 g
∴ Range = 204 – 70 = 134 g
(ii) Now forming the frequency distribution table, taking class intervals such as 70-89, 90-109, so on
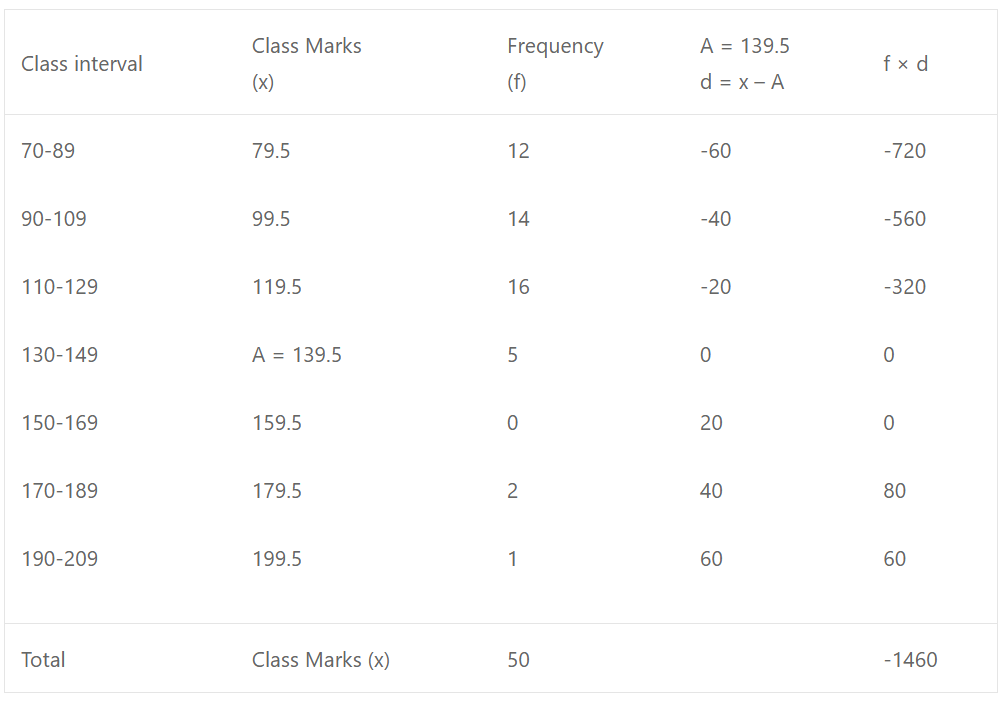
Let A = 139.5
(iii) Mean = A + [∑fd/∑f] = 139.5 + [−1460/50] = 139.5 – 29.2 = 110.3
Que-14: The following table gives the weekly wages of workers in a factory.

Calculate : (i) the mean, (ii) the number of workers getting weekly wages below Rs. 80, and (iii) the number of workers getting Rs. 65 and more but less than Rs. 85 as weekly wages.
Sol: (i) Mean = A + [∑fd/∑f] = 67.5 + [120/80] = 67.5 + 1.5 = 69
(ii) Number of workers getting wages below Rs: 80 = 60
(iii) Number of workers getting more than Rs. 65 but less them 85 = 10 + 9 + 6 + 12 = 37
![Mean = A + [∑fd/∑f] = 67.5 + [120/80] = 67.5 + 1.5 = 69 (ii) Number of workers getting wages below Rs: 80 = 60 (iii) Number of workers getting more than Rs. 65 but less them 85 = 10 + 9 + 6 + 12 = 37](https://icsehelp.com/wp-content/uploads/2025/02/14a.png)
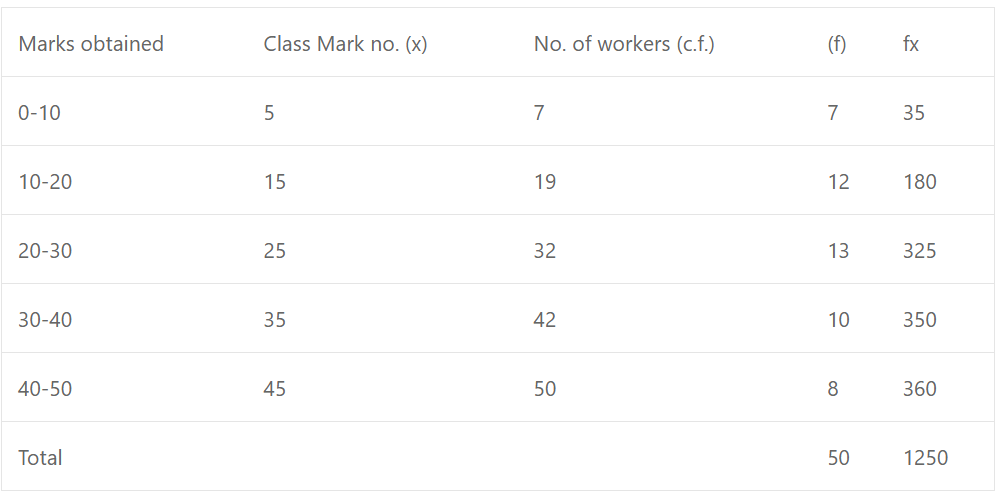
Que-15: Find the mean of the following data:

Sol: Mean = ∑fx/∑f′ = 1250/50 = 25
Que-16: Recast the following cumulative table into the form of an ordinary frequency distribution and determine the value of the mean :
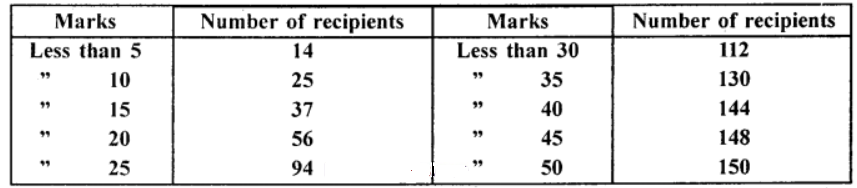
Sol: Mean = A + [∑fd/∑f] = 27.5 + [−800/150] = 27.5 – 5.3 = 22.2
![Sol: Mean = A + [∑fd/∑f] = 27.5 + [−800/150] = 27.5 – 5.3 = 22.2](https://icsehelp.com/wp-content/uploads/2025/02/16a.png)
Que-17: Find the missing frequency in the following data if arithmetic mean is 19.92.

Sol: Let the missing frequency be p, then

Mean is given = 19.92
∴ Mean = ∑fx/∑f
⇒ 19.92 = (1772+22p)/90+p
⇒ 1772 + 22p = 1792.8 + 19.92p
22p = 19.92p = 1792.8 – 1772
2.08p = 20.8
∴ p = 20.8/2.08 = (208×100)/(10×208) = 10
∴ Missing Frequency = 10
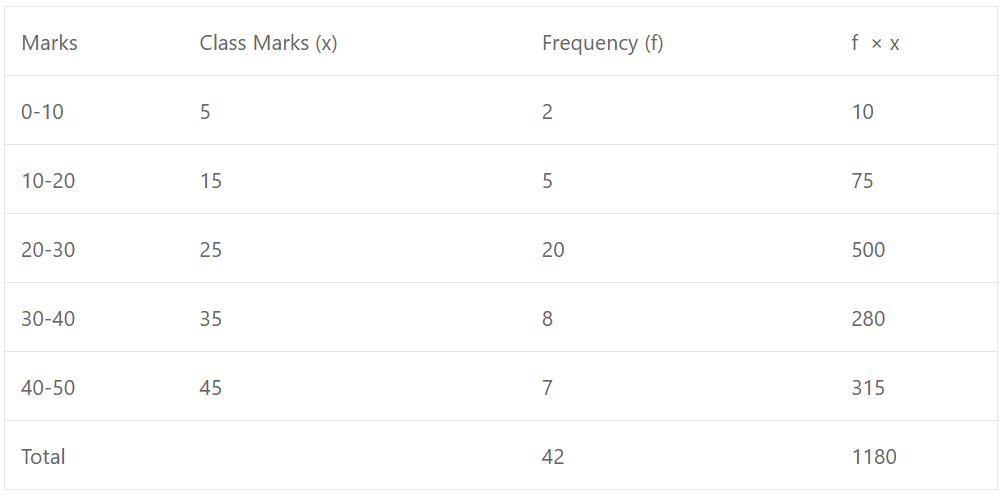
Que-18: Calculate the Arithmetic mean, correct to one decimal place, for the following frequency distribution of marks obtained in an Arithmetic test.
Sol: Mean = ∑fx/∑f = 1180/42 = 28.095 = 28.1 (approx)
Que-19: The following table gives the marks scored by students in the examination:

Calculate the mean mark, correct to two decimal places.
Sol: A = 17.5
Mean = A + [∑fd/∑] = 17.5 + [85/80] = 17.5 + 1.06 = 18.56
![Sol: A = 17.5 Mean = A + [∑fd/∑] = 17.5 + [85/80] = 17.5 + 1.06 = 18.56](https://icsehelp.com/wp-content/uploads/2025/02/19a.png)
–: End of Arithmetic Mean, Median, Mode and Quartiles Class 10 OP Malhotra Exe-18A ICSE Maths Solutions Ch-18 :–
Return to :- OP Malhotra S Chand Solutions for ICSE Class-10 Maths
Thanks
Please Share with Your Friends