Arithmetic Mean, Median, Mode and Quartiles Class 10 OP Malhotra Exe-18B ICSE Maths Solutions Ch-18 Questions as latest prescribe guideline for upcoming exam. In this article you would learn How to Find Arithmetic Median of Grouped and Ungrouped Data. Visit official Website CISCE for detail information about ICSE Board Class-10 Mathematics.

Arithmetic Median Class 10 OP Malhotra Exe-18B ICSE Maths Solutions Ch-18
| Board | ICSE |
| Publications | S Chand |
| Subject | Maths |
| Class | 10th |
| Chapter-18 | Arithmetic Mean, Median, Mode and Quartiles |
| Writer | OP Malhotra |
| Exe-18B | How to Find Arithmetic Median |
| Edition | 2024-2025 |
How to Find Arithmetic Median of Grouped and Ungrouped Data
The value of the middle-most observation obtained after arranging the data in ascending order is called the median of the data
Median Formula for Ungrouped Data
The following steps are helpful while applying the median formula for ungrouped data.
Step 1: Arrange the data in ascending or descending order.
Step 2: Secondly, count the total number of observations ‘n’.
Step 3: Check if the number of observations ‘n’ is even or odd.
Median Formula When n is Odd: Median = [(n + 1)/2]th term
Median Formula When n is Even: Median = 1/2 [ (n/2) th + ((n/2)+1) ] th term
Exercise- 18B (Arithmetic Median)
Arithmetic Mean, Median, Mode and Quartiles Class 10 OP Malhotra Exe-18B ICSE Maths Solutions Ch-18
Que-1: Find the median of the following sets of data :
(i) 2, 3, 5, 7, 9
(ii) 4, 8, 12, 16, 20, 23, 28, 32
(iii) 60, 33, 63, 61, 44, 48, 51
(iv) 13, 22, 25, 8, 11, 19, 17, 31, 16, 10 (v) First ten prime numbers
(vi) Prime numbers between 51 and 80
Sol: (i) 2, 3, 5, 7, 9
Here n = 5 which is odd
∴ Median = (n+1)/2 th term = {(5+1)/2} th term = 6/2 = 3rd term
Which is 5
∴ Median = 5
(ii) 4. 8, 12, 16, 20, 23, 28, 32
Here n = 8 which is even
∴ Median = the mean of (n/2) and ((n/2)+1) term
= 1/2[(8/2) th +((8/2)+1) th term ]
= 1/2(4 th + 5 th term )
= 1/2 [16+20] = 36/2 = 18
∴ Median = 18
(iii) 60, 33, 63, 61, 44, 48, 51
Aranging in ascending order,
35, 44, 48, 51, 60, 61, 63
Here = 7 which is odd
∴Median = (n+1)/2 th term = (7+1)/2 th term = 4th term
Which is 51
∴ Median = 51
(iv) 13. 22, 25, 8, 11, 19, 17, 31, 16, 10
Arranging in ascending order, 8, 10, 11, 13, 16, 17, 19, 22, 25, 31
Here n = 10 which is even
∴ Median = 1/2[(n/2) th +((n/2)+1) th term ]
= 1/2[(10/2) th +((10/2)+1) th term ]
= 1/2[5 th +6 th term ]
= 1/2[16+17] = (1/2)×33 = 16.5
∴ Median = 16.5
(v) First ten prime numbers which are 2, 3, 5, 7, 11, 13, 17, 19, 23, 29
∴ Median = 12/[(n/2) th + ((n/2)+1) th term ]
= 1/2[(10/2) th +((10/2)+1) th terms ]
= 1/2[5 th + 6 th terms ]
= 1/2[11+13] = 24/2 = 12
∴ Median = 12
(vi) Prime numbers between 51 and 80
Which are 53, 59, 61, 67, 71, 73, 79
Here n = 7 which is odd
∴ Median = (n+1)/2 th term = (7+1)/2 th term = 4th term which is 67
∴ Median = 67
Que-2: The following table gives the monthly incomes of 12 families in a town :

Calculate the median of the above incomes.
Sol: Arranging in ascending order,
75, 75, 80, 94, 96, 98, 100, 104, 180, 200, 280, 600
Here n = 12
∴ Median = 1/2[(n/2) th +((n/2)+1) th term ]
= 1/2[(12/2) th +((12/2)+1) th term ]
= 1/2[6 th +7 th term )
= 1/2[98+100] = 198/2 = Rs. 99
∴ Median = Rs. 99
Que-3: Calculate the median-from the following data :

Sol: Total number of workers = 120 which is even
∴Median = n/2 th term = 120/2 = 60th term
Which lies between 46 to 65 of c.f. column
∴ Median = Rs. 24

Que-4: Compute the median of the following distributions :
(i)

(ii)

Sol: (i) After arranging in ascending order,
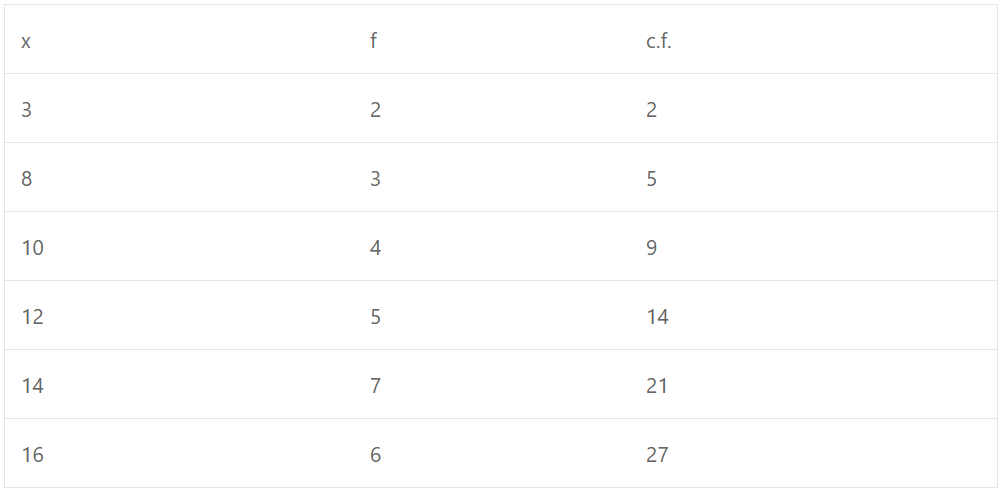
Here n = 27 which is odd
∴ Median = (n+1)/2 th term = (27+1)/2 th
= 14th term
Which lies between 15 to 21 of c.f. column
∴ Median = 12
(ii) After arranging in ascending order,
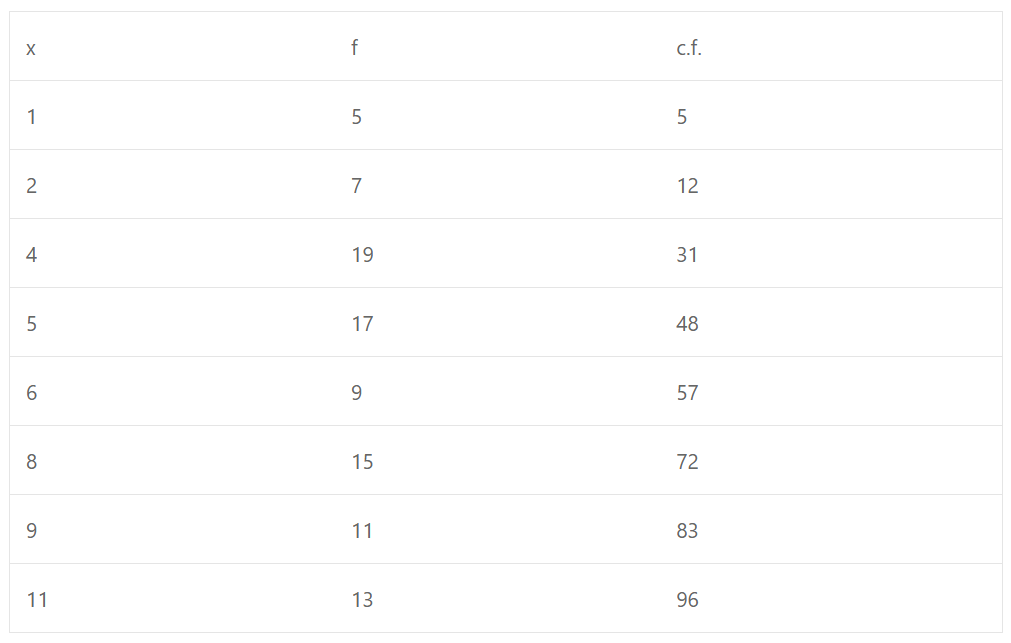
Here n = 96 which is even
∴ Median = n/2 th term = 96/2 = 48th term
which lies between 32-48 of c.f. column
∴ Median = 5 or 6
Que-5: Marks obtained by 38 students are given below. Calculate the median marks :

Sol: After arranging in ascending order

Here n = 38 which is even
∴ Median = n/2 th term = 38/2 = 19th term
Which lies between 17 – 27 of c.f columns
∴ Median = 70 marks
Que-6: Find the arithmetic mean of the first 1-0 natural numbers and show that it is equal to their median.
Sol: First 10 natural numbers are 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
∴ Mean (x¯)
= (1+2+3+4+5+6+7+8+9+10)/10 = 55/10 = 5.5
Median : Here n = 10 which is even
∴ Median = 1/2[(n/2) th + ((n/2)+1) th term ]
= 1/2[(10/2) th + ((10/2)+1) th term ]
= 1/2 [5th term + 6th term]
= 12 [5 + 6] = 11/2 = 5.5
Hence Mean = Median
Que-7: Find whether the following statement is true or false :
(i) The median of a frequency distribution is the most commonly occuring value.
(ii) The median of a discrete ungrouped frequency distribution .containing a number of items is the value of the middle item, the data being arranged in ascending or descending order.
Sol: (i) False: Median is the middle term after arranging in order.
(ii) True.
Que-8: In a school examination it is decided that exactly half the pupils will pass. Name the measure of central tendency that is used.
Sol: The measure of central tendency that is used is median
∵ Median is the n/2 or {(n+1)/2} th term which is the middle term.
Que-9: {1, 2, 3, 6, 8} is a set of five positive integers whose mean is 4 and median is 3. Write down two other sets of five positive integers, each having the same mean and median as this set.
Sol: In the given set {1,2,3,6, 8} of 5 positive integer
Here median = (5+1)/2 th term
= 6/2 th term = 3rd term
Which is 3
We can have also other sets of 5 positive integers which have the same median In other words, the third term must be 3 and first two integers will be less than 3 and last two integers can be different but there is no change in mean also So, {1, 2, 3, 4, 10}, {1, 2, 3, 5, 9} etc. can be such sets
(∵ Here sum of last two integers = sum of last two integers as in the given set)
Que-10: Find the median for the following data. 46, 64, 87, 41, 58, 77, 35, 90, 55, 33, 92 If in the data, the observation 92 is replaced by 19 determine the new median.
Sol: 46, 64, 87, 41, 58, 77, 35, 90, 55, 33, 92
(i) Arranging in ascending order,
33, 35, 41, 46, 55, 58, 64, 77, 87, 90, 92
Here n = 11 which is odd
Median = (n+1)/2 th term = (11+1)/2 th term = 6th term
Which is 58
∴ Median = 58
If we replace 92 by 19, then the number will be 19, 33, 35, 41,46, 55, 58, 64, 77, 87, 90 and then median = 6th term {as in (i)}
Which is 55
∴ Median in this case = 55
Que-11: The following data have been arranged in ascending order :
24, 27, 28, 31, 34, x, 37, 40, 42, 45 If the median of the data is 35, find x. In the above data, if 45 changed to 33, find the new median.
Sol: 24, 27, 28. 3 I, 34. v. 37, 40, 42. 45 Here n = 10 which is even
∴ Median = 1/2[(n/2) th + ((n/2)+1) th term ]
= 1/2[(10/2) th +((10/2)+1) th term ]
= 1/2 [5th + 6th terms] = 1/2 (34 + x)
= (1/2) × (34 + x) = 35 ⇒ 17 + (x/2) = 35
= (x/2) = 35 – 17 = 18 ⇒ x = 36
If 45 is replaced by 33, then
24, 27, 28, 31, 33, 34, 36, 37, 40, 42
Median = 1/2(5th + 6th term)
= 1/2 (33 + 34) = (1/2) × 67 = 33.5
∴ New median = 33.5
Que-12: The median of the following observation arranged in ascending order is 24. Find x. 11, 12, 14, 18, x + 2, x + 4, 30, 32, 35, 41.
Sol: 11, 12, 14, 18, x + 2, A + 4, 30, 32, 35, 41
Here n = 10
∴ Median = 1/2[(n/2) th +((n/2)+1) th term ]
= 1/2[(10/2) th +((10/2)+1) th term ]
= 1/2 [5th + 6th term]
= 1/2 (x + 2 + x + 4) = 1/2 (x + 6) = x + 3
∴ x + 3 = 24 ⇒ x = 24 – 3 = 21
Hence x = 21
–: End of Arithmetic Mean, Median, Mode and Quartiles Class 10 OP Malhotra Exe-18B ICSE Maths Solutions Ch-18 :–
Return to :- OP Malhotra S Chand Solutions for ICSE Class-10 Maths
Thanks
Please Share with Your Friends


