Banking Exe-2B Class-10 Concise ICSE Mathematics Selina Solution Ch-2. We Provide Step by Step Solutions / Answer of Exe-2(B) Banking of Selina Concise Maths . Visit official Website CISCE for detail information about ICSE Board Class-10 Mathematics.

Banking Exe-2B Class-10 Concise ICSE Mathematics Selina Solution Ch-2
| Board | ICSE |
| Publications | Selina |
| Subject | Maths |
| Class | 10th |
| Chapter-2 | Banking |
| Writer | R.K. Bansal |
| Exe-2B | Solved Complex Questions on Recurring Deposit |
| Edition | 2025-2026 |
Exe-2B Complex Questions on Recurring Deposit
Banking Exe-2B Class-10 Concise ICSE Mathematics Selina Solution Ch-2
Que-1. Pramod deposits 600 per month in a Recurring Deposit Account for 4 years. If the rate of interest is 8% per year; calculate the maturity value of his account.
Ans- Instalment per month(P) = Rs 600
Number of months(n) = 48
Rate of interest(r)= 8%p.a.
∴ SI = P x [n(n+1)/2 x 12] x r/100
=> 600 x [48(48+1)/2 x 12] x 8/100
=> Rs 4704
The amount that Pramod will get at the time of maturity
=Rs(600×48)+ Rs 4,704
=Rs 28,800+ Rs 4,704
= Rs 33,504
Que-2. Ritu has a Recurring Deposit Account in a bank and deposits Rs. 80 per month for 18 months. Find the rate of interest paid by the bank if the maturity value of account is Rs 1,554.
Ans- Installment per month(P) = Rs 80
Number of months(n) = 18
Let rate of interest(r)= r %p.a.
∴ SI = P x [n(n+1)/2 x 12] x r/100
=> 80x [18(18+1)/2 x 12] x r/100
=> Rs 11.4r
Maturity value= Rs(80 x18)+Rs(11.4r)
Given maturity value= Rs1,554
Then Rs(80 x18)+Rs(11.4r) = Rs1,554
11.4r = Rs1,554 – Rs1,440
=> r = 114/11.4 = 10
Que-3. The maturity value of a R.D. Account is Rs 16,176. If the monthly installment is Rs 400 and the rate of interest is 8%; find the time (period) of this R.D Account.
Ans- Installment per month(P) = Rs400
Number of months(n) = n
Let rate of interest(r)= 8 %p.a.
∴ SI = P x [n(n+1)/2 x 12] x r/100
=> 400x [n(n+1)/2 x 12] x 8/100
=> Rs 4n(n+1)/3
Given maturity value= Rs16,176
ThenRs(400x n)+ = Rs16,176
1200n +4n²+4n= Rs48,528
4n²+1204n = Rs48,528
n²+301n – 12132= 0
(n+337)(n-36)=0
n= -337 or n=36
Then number of months = 36 months= 3 years Ans.
Que-4. Mr. Bajaj needs Rs 30,000 after 2 years. What least money (in multiple of Rs 5) must he deposit every month in a recurring deposit account to get required money after 2 years, the rate of interest being 8% p.a.?
Ans- Let installment per month= Rs P
Number of months(n) = 24
Rate of interest= 8%p.a.
∴ SI = P x [n(n+1)/2 x 12] x r/100
=> Px [24(24+1)/2 x 12] x 8/100
=> Rs 2P
Maturity value= Rs(P x 24)+ Rs 2P= Rs26P
Given maturity value= Rs30,000
26P = 30000
=> P = 30000/26 = rs 1155 (multiple of 5)
Que-5. Mr. Richard has a recurring deposit account in a post office for 3 years at 7.5% p.a. simple interest. If he gets Rs. 8,325 as interest at the time of maturity, find: the monthly income , the amount of maturity.
Ans- Let the monthly deposit be P
Interest = Rs. 8,325
Rate of interest = 7.5%
Time = 3 years = 36 months
∴ SI = P x [n(n+1)/2 x 12] x r/100
=> 8325 = P x [36(36+1)/2 x 12] x 7.5/100
=> P = Rs 2000
(ii) MV = total sum + SI
=> 2000 x 36 + 8325
=> Rs 80325
Que-6. Gopal has a cumulative deposit account and deposits Rs 900 per month for a period of 4 years he gets Rs 52,020 at the time of maturity, find the rate of interest.
Ans- Installment per month(P) = Rs 900
Number of months(n) = 48
Let rate of interest(r)= r %p.a.
∴ SI = P x [n(n+1)/2 x 12] x r/100
=> 900 x [48(48+1)/2 x 12] x r/100
=> Rs 882 r
Maturity value= Rs(900 x 48)+Rs(882)r
Given maturity value= Rs 52,020
Then Rs(900 x 48)+Rs(882)r = Rs 52,020
882r = Rs 52,020 – Rs43,200
r = 8820/882 = 10
Que-7. Deepa has a 4-year recurring deposit account in a bank and deposits Rs 1,800 per month. If she gets Rs 1,08,450 at the time of maturity, find the rate of interest.
Ans- Installment per month(P) = Rs1,800
Number of months(n) = 48
Let rate of interest(r)= r %p.a.
∴ SI = P x [n(n+1)/2 x 12] x r/100
=> 1800x [48(48+1)/2 x 12] x r/100
=> Rs 1764 r
Maturity value= Rs(1,800 x48)+Rs(1,764)r
Given maturity value= Rs1,08,450
Then Rs(1,800 x48)+Rs(1764)r = Rs1,08,450
1764r = Rs1,08,450 – Rs86,400
r = 22050/1764 = 12.5
Que-8. Mr. Britto deposits a certain sum of money each month in a Recurring Deposit Account of a bank. If the rate of interest is of 8% per annum and Mr. Britto gets Rs. Rs 8,088 from the bank after 3 years, find the value of his monthly instalment.
Ans-
Let the value of the monthly Instalment be Rs P
Number of months(n) = 3 x 12 = 36 months
Let rate of interest(r)= 8 %p.a.
MV = Rs 8088
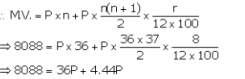
P = 8088/40.44 = 200
Thus the value of his monthly income is Rs 200.
Que-9. Sharukh opened a Recurring Deposit Account in a bank and deposited Rs. 800 per month for 1(1/2) years. If he received Rs. 15084 at the time of maturity , find the rate of interest per annum.
Ans- Monthly deposit (P) = Rs 800
n = 3/2 x 12 = 18 months
MV = Rs 15084
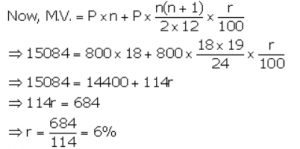
Thus rate of interest per annum is 6
Que-10. Katrina opened a recurring deposit account with a Nationalised Bank for a period of 2 years. If the bank pays interest at the rate of 6% per annum and the monthly installment is Rs. 1,000, find the : (i) interest earned in 2 years (ii) maturity value
Ans- P = 1000|
n = 2 x 12 = 24 months
SI = 6370
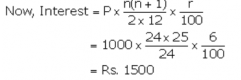
Thus the interest earned in 2 years is Rs 1500
(ii) Total money deposited in the bank = 24 x 1000 = 24000
MV = 24000 + 1500 = Rs 25500
Que-11. Mohan has a recurring deposit account in a bank for 2 years at 6% p.a. simple interest. If he gets Rs. 1,200 as interest at the time of maturity, find: (i) the monthly instalment (ii) the amount of maturity.
Ans- Interest, I = Rs. 1,200
Time, n = 2 years = 2 × 12 = 24 months
Rate, r = 6%
(i) To find: Monthly instalment, P
Now,

So, the monthly instalment is Rs. 800.
(ii) Total sum deposited = P × n = Rs. 800 × 24 = Rs. 19,200
∴ Amount of maturity = Total sum deposited + Interest on it
= Rs. (19,200 + 1,200)
= Rs. 20,400
— : End of Banking Exe-2B Class-10 Concise ICSE Mathematics Selina Ch-2. Step by Step Solutions :–
Return to :- Selina Concise Solutions for ICSE Class-10 Maths
Thanks
Please Share with Your Friends


