ML Aggarwal Expansions Exe-3.1 Class 9 ICSE Maths Solutions. We Provide Step by Step Answer of Exe-3.1 Questions for as council prescribe guideline for upcoming exam . Visit official website CISCE for detail information about ICSE Board Class-9.
ML Aggarwal Expansions Exe-3.1 Class 9 ICSE Maths Solutions
| Board | ICSE |
| Subject | Maths |
| Class | 9th |
| Chapter-3 | Expansions |
| Topics | Solution of Exe-3.1 Questions |
| Edition | 2024-2025 |
Problems on Expansion
ML Aggarwal Exe-3.1 Class 9 ICSE Maths Solutions
Question 1.
(i) (2x + 7y)2
(ii) (1/2 x + 2/3 y)2
Answer :
(i) (2x + 7y)2
It can be written as
= (2x)2 + 2 × 2x × 7y + (7y)2
So we get
= 4x2 + 28xy + 49y2
(ii) (1/2 x + 2/3 y)2
It can be written as
= (1/2 x)2 + 2 × ½x + 2/3y + (2/3 y)2
So we get
= ¼ x2 + 2/3 xy + 4/9 y2
Question 2.
(i) (3x + 1/2x)2
(ii) (3x2y + 5z)2
Answer :
(i) (3x + 1/2x)2
It can be written as
= (3x)2 + 2 × 3x × 1/2x + (1/2x)2
So we get
= 9x2 + 3 + 1/4x2
= 9x2 + 1/4x2 + 3
(ii) (3x2y + 5z)2
It can be written as
= (3x2y)2 + 2 × 3x2y × 5z + (5z)2
So we get
= 9x4y2 + 30x2yz + 25z2
Question 3.
(i) (3x – 1/2x)2
(ii) (1/2 x – 3/2 y)2
Answer :
(i) (3x – 1/2x)2
It can be written as
= (3x)2 – 2 × 3x × 1/2x + (1/2x)2
So we get
= 9x2 – 3 + 1/4x2
= 9x2 + 1/4x2 – 3
(ii) (1/2 x – 3/2 y)2
It can be written as
= (1/2 x)2 + (3/2 y)2 – 2 × ½ x × 3/2 y
So we get
= ¼ x2 + 9/4 y2 – 3/2 xy
= ¼ x2 – 3/2 xy + 9/4 y2
Question 4.
(i) (x + 3) (x + 5)
(ii) (x + 3) (x – 5)
(iii) (x – 7) (x + 9)
(iv) (x – 2y) (x – 3y)
Answer :
(i) (x + 3) (x + 5)
By further calculation
= x2 + (3 + 5) x + 3 × 5
So we get
= x2 + 8x + 15
(ii) (x + 3) (x – 5)
By further calculation
= x2 + (3 – 5)x – 3 × 5
So we get
= x2 – 2x – 15
(iii) (x – 7) (x + 9)
By further calculation
= x2 – (7 – 9)x – 7 × 9
So we get
= x2 + 2x – 63
(iv) (x – 2y) (x – 3y)
By further calculation
= x2 – (2y + 3y)x + 2y × 3y
So we get
= x2 – 5xy + 6y2
Question 5.
(i) (x – 2y – z)2
(ii) (2x – 3y + 4z)2
Answer :
(i) (x – 2y – z)2
It can be written as
= [x + (-2y) + (-z)]2
By further calculation
= (x)2 + (-2y)2 + (-z)2 + 2 × x × (-2y) + 2 × (-2y) × (-z) + 2 × (-z) × x
So we get
= x2 + 4y2 + z2 – 4xy + 4yz – 2zx
(ii) (2x – 3y + 4z)2
It can be written as
= [2x + (-3y) + 4z]2
By further calculation
= (2x)2 + (-3y)2 + (4z)2 + 2 × 2x × (-3y) + 2 × (-3y) × 4z + 2 × 4z × 2x
So we get
= 4x2 + 9y2 + 16z2 -12xy – 24yz + 16zx
Question 6.
(i) (2x + 3/x – 1)2
(ii) (2/3 x – 3/2x – 1)2
Answer :
(i) (2x + 3/x – 1)2
It can be written as
= [2x + 3/x + (-1)]2
By further calculation
= (2x)2 + (3/x)2 + (-1)2 + 2 ×2x × 3/x + 2 × 3/x × (-1) + 2 × (-1) × 2x
So we get
= 4x2 + 9/x2 + 1 + 12 – 6/x – 4x
= 4x2 + 9/x2 + 13 – 6/x – 4x
(ii) (2/3 x – 3/2x – 1)2
It can be written as
= [2/3 x – 3/2x – 1]2
By further calculation
= (2/3 x)2 + (-3/2x)2 + (-1)2 + 2 × 2/3 x × (-3/2x) + 2 × (-3/2x) × (-1) + 2 × (-1) × (2/3 x)
So we get
= 4/9 x2 + 9/4x2 + 1 – 2 + 3/x – 4/3 x
= 4/9 x2 + 9/4x2 – 1 – 4/3 x + 3/x
Question 7.
(i) (x + 2)3
(ii) (2a + b)3
Answer :
(i) (x + 2)3
It can be written as
= x3 + 23 + 3 × x × 2 (x + 2)
By further calculation
= x3 + 8 + 6x (x + 2)
So we get
= x3 + 8 + 6x2 + 12x
= x3 + 6x2 + 12x + 8
(ii) (2a + b)3
It can be written as
= (2a)3 + b3 + 3 × 2a × b (2a + b)
By further calculation
= 8a3 + b3 + 6ab (2a + b)
So we get
= 8a3 + b3 + 12a2b + 6ab2
Question 8.
(i) (3x + 1/x)3
(ii) (2x – 1)3
Answer :
(i) (3x + 1/x)3
It can be written as
= (3x)3 + (1/x)3 + 3 × 3x × 1/x (3x + 1/x)
By further calculation
= 27x3 + 1/x3 + 9 (3x + 1/x)
So we get
= 27x3 + 1/x3 + 27x + 9/x
(ii) (2x – 1)3
It can be written as
= (2x)3 – 13 – 3 × 2x × 1 (2x – 1)
By further calculation
= 8x3 – 1 – 6x (2x – 1)
So we get
= 8x3 – 1 – 12x2 + 6x
= 8x3 – 12x2 + 6x – 1
Question 9.
(i) (5x – 3y)3
(ii) (2x – 1/3y)3
Answer :
(i) (5x – 3y)3
It can be written as
= (5x)3 – (3y)3 – 3 × 5x × 3y (5x – 3y)
By further calculation
= 125x3 – 27y3 – 45xy (5x – 3y)
So we get
= 125x3 – 27y3 – 225x2y + 135xy2
(ii) (2x – 1/3y)3
It can be written as
= (2x)3 – (1/3y)3 – 3 × 2x × 1/3y (2x – 1/3y)
By further calculation
= 8x3 – 1/27y3 – 2x/y (2x – 1/3y)
So we get
= 8x3 – 1/27y3 – 4x2/y + 2x/3y2
Simplify the following (10 to 19):
Question 10.
(i) (a + b)2 + (a – b)2
(ii) (a + b)2 – (a – b)2
Answer :
(i) (a + b)2 + (a – b)2
It can be written as
= (a2 + b2 + 2ab) + (a2 +b2 – 2ab)
By further calculation
= a2 + b2 + 2ab + a2 + b2 – 2ab
So we get
= 2a2 + 2b2
Taking 2 as common
= 2 (a2 + b2)
(ii) (a + b)2 – (a – b)2
It can be written as
= (a2 + b2 + 2ab) – (a2 + b2 – 2ab)
By further calculation
= a2 + b2 + 2ab – a2 – b2 + 2ab
So we get
= 4ab
Question 11.
(i) (a + 1/a)2 + (a – 1/a)2
(ii) (a + 1/a)2 – (a – 1/a)2
Answer :
(i) (a + 1/a)2 + (a – 1/a)2
It can be written as
= [a2 + (1/a)2 + 2 × a × 1/a] + [a2 + (1/a)2 – 2 × a × 1/a]
By further calculation
= [a2 + 1/a2 + 2] + [a2 + 1/a2 – 2]
So we get
= a2 + 1/a2 + 2 + a2 + 1/a2 – 2
= 2a2 + 2/a2
Taking 2 as common
= 2 (a2 + 1/a2)
(ii) (a + 1/a)2 – (a – 1/a)2
It can be written as
= [a2 + (1/a)2 + 2 × a × 1/a] – [a2 + (1/a)2 – 2 × a × 1/a]
By further calculation
= [a2 + 1/a2 + 2] – [a2 + 1/a2 – 2]
So we get
= a2 + 1/a2 + 2 – a2 – 1/a2 + 2
= 4
Question 12.
(i) (3x – 1)2 – (3x – 2) (3x + 1)
(ii) (4x + 3y)2 – (4x – 3y)2 – 48xy
Answer :
(i) (3x – 1)2 – (3x – 2) (3x + 1)
It can be written as
= [(3x)2 + 12 – 2 × 3x × 1] – [(3x)2 – (2 – 1) (3x) – 2 × 1]
By further calculation
= [9x2 + 1 – 6x] – [9x2 – 3x – 2]
So we get
= 9x2 + 1 – 6x – 9x2 + 3x + 2
= -3x + 3
= 3 – 3x
(ii) (4x + 3y)2 – (4x – 3y)2 – 48xy
It can be written as
= [(4x)2 + (3y)2 + 2 × 4x × 4y] – [(4x)2 + (3y)2 – 2 × 4x × 3y] – 48xy
By further calculation
= [16x2 + 9y2 + 24xy] – [16x2 + 9y2 – 24xy] – 48xy
So we get
= 16x2 + 9y2 + 24xy – 16x2 – 9y2 + 24xy – 48xy
= 0
Question 13.
(i) (7p + 9q) (7p – 9q)
(ii) (2x – 3/x) (2x + 3/x)
Answer :
(i) (7p + 9q) (7p – 9q)
It can be written as
= (7p)2 – (9q)2
= 49p2 – 81q2
(ii) (2x – 3/x) (2x + 3/x)
It can be written as
= (2x)2 – (3/x)2
= 4x2 – 9/x2
Question 14.
(i) (2x – y + 3) (2x – y – 3)
(ii) (3x + y – 5) (3x – y – 5)
Answer :
(i) (2x – y + 3) (2x – y – 3)
It can be written as
= [(2x – y) + 3] [(2x – y) – 3]
= (2x – y)2 – 32
By further calculation
= (2x)2 +y2 – 2 × 2x × y – 9
So we get
= 4x2 + y2 – 4xy – 9
(ii) (3x + y – 5) (3x – y – 5)
It can be written as
= [(3x – 5) + y] [(3x – 5) – y]
= (3x – 52) – y2
By further calculation
= (3x)2 + 52 – 2 × 3x × 5 – y2
So we get
= 9x2 + 25 – 30x – y2
= 9x2 – y2 – 30x + 25
Question 15.
(i) (x + 2/x – 3) (x – 2/x – 3)
(ii) (5 – 2x) (5 + 2x) (25 + 4x2)
Answer :
(i) (x + 2/x – 3) (x – 2/x – 3)
It can be written as
= [(x – 3) + (2/x)] [(x – 3) – (2/x)]
= (x – 3)2 – (2/x)2
Expanding using formula
= x2 + 9 – 2 × x × 3 – 4/x2
By further calculation
= x2 + 9 – 6x – 4/x2
So we get
= x2 – 4/x2 – 6x + 9
(ii) (5 – 2x) (5 + 2x) (25 + 4x2)
It can be written as
= [52 – (2x)2] (25 + 4x2)
By further calculation
= (25 – 4x2) (25 + 4x2)
So we get
= 252 – (4x2)2
= 625 – 16x4
Question 16.
(i) (x + 2y + 3) (x + 2y + 7)
(ii) (2x + y + 5) (2x + y – 9)
(iii) (x – 2y – 5) (x – 2y + 3)
(iv) (3x – 4y – 2) (3x – 4y – 6)
Answer :
(i) (x + 2y + 3) (x + 2y + 7)
Consider x + 2y = a
(a + 3) (a + 7) = a2 + (3 + 7) a + 3 × 7
By further calculation
= a2 + 10a + 21
Substituting the value of a
= (x + 2y)2 + 10 (x + 2y) + 21
By expanding using formula
= x2 + 4y2 + 2 × x × 2y + 10x + 20y + 21
So we get
= x2 + 4y2 + 4xy + 10x + 20y + 21
(ii) (2x + y + 5) (2x + y – 9)
Consider 2x + y = a
(a + 5) (a – 9) = a2 + (5 – 9) a + 5 × (-9)
By further calculation
= a2 – 4a – 45
Substituting the value of a
= (2x + y)2 – 4 (2x + y) – 45
By expanding using formula
= 4x2 + y2 + 2 × 2x × y – 8x – 4y – 45
So we get
= 4x2 + y2 + 4xy – 8x – 4y – 45
(iii) (x – 2y – 5) (x – 2y + 3)
Consider x – 2y = a
(a – 5) (a + 3) = a2 + (- 5 + 3) a + (-5) (3)
By further calculation
= a2 – 2a – 15
Substituting the value of a
= (x – 2y)2 – 2 (x – 2y) – 15
By expanding using formula
= x2 + 4y2 – 2 × x × 2y – 2x + 4y – 15
So we get
= x2 + 4y2 – 4xy – 2x + 4y – 15
(iv) (3x – 4y – 2) (3x – 4y – 6)
Consider 3x – 4y = a
(a – 2) (a – 6) = a2 (- 2 – 6)a + (-2) (-6)
By further calculation
= a2 – 8a + 12
Substituting the value of a
= (3x – 4y)2 – 8 (3x – 4y) + 12
Expanding using formula
= 9x2 + 16y2 – 2 × 3x × 4y – 24x + 32y + 12
So we get
= 9x2 + 16y2 – 24xy – 24x + 32y + 12
Question 17.
(i) (2p + 3q) (4p2 – 6pq + 9q2)
(ii) (x + 1/x) (x2 – 1 + 1/x2)
Answer :
(i) (2p + 3q) (4p2 – 6pq + 9q2)
It can be written as
= (2p + 3q) [(2p)2 – 2p × 3q + (3q)2]
By further simplification
= (2p)3 + (3q)3
= 8p3 + 27q3
(ii) (x + 1/x) (x2 – 1 + 1/x2)
It can be written as
= (x + 1/x) [x2 – x × 1/x + (1/x)2]
By further simplification
= x3 + (1/x)3
= x3 + 1/x3
Question 18.
(i) (3p – 4q) (9p2 + 12pq + 16q2)
(ii) (x – 3/x) (x2 + 3 + 9/x2)
Answer :
(i) (3p – 4q) (9p2 + 12pq + 16q2)
It can be written as
= (3p – 4q) [(3p)2 + 3p × 4q + (4q)2]
By further simplification
= (3p)3 – (4q)3
= 27p3 – 64q3
(ii) (x – 3/x) (x2 + 3 + 9/x2)
It can be written as
= (x – 3/x) [x2 + x × 3/x + (3/x)2]
By further simplification
= x3 – (3/x)3
= x3 – 27/x3
Question 19. (2x + 3y + 4z) (4x2 + 9y2 + 16z2 – 6xy – 12yz – 8zx).
Answer :
(2x + 3y + 4z) (4x2 + 9y2 + 16z2 – 6xy – 12yz – 8zx)
It can be written as
= (2x + 3y + 4z) ((2x)2 + (3y)2 + (4z)2 – 2x × 3y – 3y × 4z – 4z × 2x)
By further calculation
= (2x)3 + (3y)3 + (4z)3 – 3 × 2x × 3y × 4z
So we get
= 8x3 + 27y3 + 64z3 – 72xyz
Question 20. Find the product of the following:
(i) (x + 1) (x + 2) (x + 3)
(ii) (x – 2) (x – 3) (x + 4)
Answer :
(i) (x + 1) (x + 2) (x + 3)
It can be written as
= x3 + (1 + 2 + 3)x2 + (1 × 2 + 2 × 3 + 3 × 1) x + 1 × 2 × 3
By further calculation
= x3 + 6x2 + (2 + 6 + 3)x + 6
So we get
= x3 + 6x2 + 11x + 6
(ii) (x – 2) (x – 3) (x + 4)
It can be written as
= x3 + (- 2 – 3 + 4) x2 + [(-2) × (-3) + (-3) × 4 + 4 × (-2)]x + (-2) (-3) (4)
By further calculation
= x3 – x2 + (6 – 12 – 8)x + 24
= x3 – x2 – 14x + 24
Question 21. Find the coefficient of x2 and x in the product of (x – 3) (x + 7) (x – 4).
Answer :
It is given that
(x – 3) (x + 7) (x – 4)
By further calculation
= x3 + (- 3 + 7 – 4) x2 + [(-3) (7) + 7 × (-4) + (-4) (-3) + (-3) (7) (-4)]
It can be written as
= x3 + 0x2 + (- 21 – 28 + 12) x + 84
So we get
= x3 + 0x2 – 37x + 84
Hence, coefficient of x2 is zero and coefficient of x is – 3.
Question 22. If a2 + 4a + x = (a + 2)2, find the value of x.
Answer :
It is given that
a2 + 4a + x = (a + 2)2
By expanding using formula
a2 + 4a + x = a2 + 22 + 2 × a × 2
By further calculation
a2 + 4a + x = a2 + 4 + 4a
So we get
x = a2 + 4 + 4a – a2 – 4a
x = 4
Question 23. Use (a + b)2 = a2 + 2ab + b2 to evaluate the following:
(i) (101)2
(ii) (1003)2
(iii) (10.2)2
Answer :
(i) (101)2
It can be written as
= (100 + 1)2
Expanding using formula
= 1002 + 12 + 2 × 100 × 1
By further calculation
= 10000 + 1 + 200
= 10201
(ii) (1003)2
It can be written as
= (1000 + 3)2
Expanding using formula
= 10002 + 32 + 2 × 1000 × 3
By further calculation
= 1000000 + 9 + 6000
= 1006009
(iii) (10.2)2
It can be written as
= (10 + 0.2)2
Expanding using formula
= 102 + 0.22 + 2 × 10 × 0.2
By further calculation
= 100 + 0.04 + 4
= 104.04
Expansions Exe-3.2
ML Aggarwal Class 9 ICSE Maths Solutions
Page 77
Question 24. Use (a – b)2 = a2 – 2ab – b2 to evaluate the following:
(i) (99)2
(ii) (997)2
(iii) (9.8)2
Answer :
(i) (99)2
It can be written as
= (100 – 1)2
Expanding using formula
= 1002 – 2 × 100 × 1 + 12
By further calculation
= 10000 – 200 + 1
= 9801
(ii) (997)2
It can be written as
= (1000 – 3)2
Expanding using formula
= 10002 – 2 × 1000 × 3 + 32
By further calculation
= 1000000 – 6000 + 9
= 994009
(iii) (9.8)2
It can be written as
= (10 – 0.2)2
Expanding using formula
= 102 – 2 × 10 × 0.2 + 0.22
By further calculation
= 100 – 4 + 0.04
= 96.04
Question 25. By using suitable identities, evaluate the following:
(i) (103)3
(ii) (99)3
(iii) (10.1)3
Answer :
(i) (103)3
It can be written as
= (100 + 3)3
Expanding using formula
= 1003 + 33 + 3 × 100 × 3 (100 + 3)
By further calculation
= 1000000 + 27 + 900 × 103
So we get
= 1000000 + 27 + 92700
= 1092727
(ii) (99)3
It can be written as
= (100 – 1)3
Expanding using formula
= 1003 – 13 – 3 × 100 × 1 (100 – 1)
By further calculation
= 1000000 – 1 – 300 × 99
So we get
= 1000000 – 1 – 29700
= 1000000 – 29701
= 970299
(iii) (10.1)3
It can be written as
= (10 + 0.1)3
Expanding using formula
= 103 + 0.13 + 3 × 10 × 0.1 (10 + 0.1)
By further calculation
= 1000 + 0.001 + 3 × 10.1
So we get
= 1000 + 0.001 + 30.3
= 1030.301
Question 26. If 2a – b + c = 0, prove that 4a2 – b2 + c2 + 4ac = 0.
Answer :
It is given that
2a – b + c = 0
2a + c = b
By squaring on both sides
(2a + c)2 = b2
Expanding using formula
(2a)2 + 2 × 2a × c + c2 = b2
By further calculation
4a2 + 4ac + c2 = b2
So we get
4a2 – b2 + c2 + 4ac = 0
Hence, it is proved.
Question 27. If a + b + 2c = 0, prove that a3 + b3 + 8c3 = 6abc.
Answer :
It is given that
a + b + 2c = 0
We can write it as
a + b = – 2c
By cubing on both sides
(a + b)3 = (-2c)3
Expanding using formula
a3 + b3 + 3ab (a + b) = -8c3
Substituting the value of a + b
a3 + b3 + 3ab (-2c) = -8c3
So we get
a3 + b3 + 8c3 = 6abc
Hence, it is proved.
Question 28. If a + b + c = 0, then find the value of a2/bc + b2/ca + c2/ab.
Answer :
It is given that
a + b + c = 0
We can write it as
a3 + b3 + c3 – 3abc = 0
a3 + b3 + c3 = 3abc
Now dividing by abc on both sides
a3/abc + b3/abc + c3/abc = 3
By further calculation
a2/bc + b2/ac + c2/ab = 3
Therefore, the value of a2/bc + b2/ca + c2/ab is 3.
Question 29. If x + y = 4, then find the value of x3 + y3 + 12xy – 64.
Answer :
It is given that
x + y = 4
By cubing on both sides
(x + y)3 = 43
Expanding using formula
x3 + y3 + 3xy (x + y) = 64
Substituting the value of x + y
x3 + y3 + 3xy (4) = 64
So we get
x3 + y3 + 12xy – 64 = 0
Hence, the value of x3 + y3 + 12xy – 64 is 0.
Question 30. Without actually calculating the cubes, find the values of:
(i) (27)3 + (-17)3 + (-10)3
(ii) (-28)3 + (15)3 + (13)3
Answer :
(i) (27)3 + (-17)3 + (-10)3
Consider a = 27, b = – 17 and c = – 10
We know that
a + b + c = 27 – 17 – 10 = 0
So a + b + c = 0
a3 + b3 + c3 = 3abc
Substituting the values
273 + (-17)3 + (-10)3 = 3 (27) (-17) (- 10)
= 13770
(ii) (-28)3 + (15)3 + (13)3
Consider a = – 28, b = 15 and c = 13
We know that
a + b + c = – 28 + 15 + 13 = 0
So a + b + c = 0
a3 + b3 + c3 = 3abc
Substituting the values
(-28)3 + (15)3 + (13)3 = 3 (- 28) (15) (13)
= – 16380
Question 31. Using suitable identity, find the value of:
= x + y
Substituting the values
= 86 + 14
= 100
— : End of ML Aggarwal Expansions Exe-3.1 Class 9 ICSE Maths Solutions :–
Return to :- ML Aggarawal Maths Solutions for ICSE Class-9
Thanks
Please Share with Your Friends
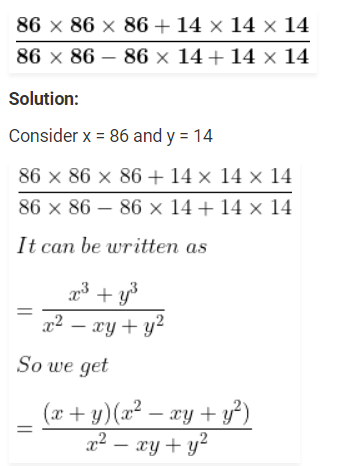



Was a great help for my assignments…..but I had 1 issue …..could you please get clear pictures cause many of them I had trouble finding them out….they are hazy..
after lock down over in India Expnasion of ML Aggarwal will be updated as 2020-21 in place of 2019-20 please wait however if emergency we can send image of limited questions
Very good 👍 website.beter than byjus and every other