ML Aggarwal Pythagoras Theorem Chapter Test Class 9 ICSE Maths Solutions

ML Aggarwal Pythagoras Theorem Chapter Test Class 9 ICSE Maths Solutions Ch-12. Step by Step Solutions of Exercise-12 Chapter-Test Questions on Pythagoras Theorem of ML Aggarwal for ICSE Class 9th Mathematics. Visit official website CISCE for detail information about ICSE Board Class-9.

ML Aggarwal Pythagoras Theorem Chapter Test Class 9 ICSE Maths Solutions Ch-12

Board	ICSE
Subject	Maths
Class	9th
Chapter-12	Pythagoras Theorem
Topics	Solution of Ch-Test Questions
Academic Session	2024-2025

Solutions of Ch-Test Questions on Pythagoras Theorem

Question 1.

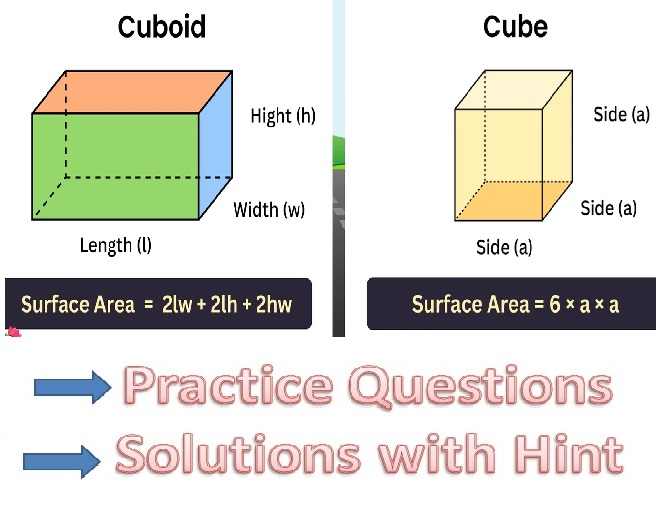
(a) In fig. (i) given below, AD ⊥ BC, AB = 25 cm, AC = 17 cm and AD = 15 cm. Find the length of BC.

(b) In figure (ii) given below, ∠BAC = 90°, ∠ADC = 90°, AD = 6 cm, CD = 8 cm and BC = 26 cm. Find :
(i) AC (ii) AB (iii) area of the shaded region.

(c) In figure (iii) given below, triangle ABC is right angled at B. Given that AB = 9 cm, AC = 15 cm and D, E are mid-points of the sides AB and AC respectively, calculate
(i) the length of BC (ii) the area of ∆ ADE.

Answer :

(a) Given AD ⊥ BC, AB = 25 cm, AC = 17 cm and AD = 15 cm

ADC is a right triangle.

⇒ 17² = 15²+DC²

⇒ 289 = 225+DC²

⇒ DC² = 289-225

⇒ DC² = 64

Taking square root on both sides,

DC = 8 cm

ADB is a right triangle.

⇒ 25² = 15²+BD²

⇒ 625 = 225+ BD²

⇒ BD² = 625-225 = 400

BD = 20 cm

⇒ BC = BD+DC

= 20+8

= 28 cm

Hence the length of BC is 28 cm.

(b) Given BAC = 90°, ADC = 90°

AD = 6 cm, CD = 8 cm and BC = 26 cm.

(i) ADC is a right triangle.

⇒ AC² = 6²+8²

⇒ AC² = 36+64

⇒ AC² = 100

Taking square root on both sides,

AC = 10 cm

Hence length of AC is 10 cm.

(ii) ABC is a right triangle.

⇒ 26² = 10²+AB²

⇒ AB² = 26²-10²

⇒ AB² = 676-100

⇒ AB² = 576

Taking square root on both sides,

AB = 24 cm

Hence length of AB is 24 cm.

(iii) Area of ABC = ½ ×AB×AC

= ½ ×24×10

= 120 cm²

Area of ADC = ½ ×AD×DC

= ½ ×6×8

= 24 cm²

Area of shaded region = area of ABC- area of ADC

= 120-24

= 96 cm²

Hence, the area of shaded region is 96 cm².

(c) Given B = 90°

AB = 9 cm, AC = 15 cm .

D, E are mid-points of the sides AB and AC respectively.

(i) ABC is a right triangle.

⇒ 15² = 9²+BC²

⇒ 225 = 81+BC²

⇒ BC² = 225-81

⇒ BC² = 144

Taking square root on both sides,

BC = 12 cm

Hence, the length of BC is 12 cm.

(ii) AD = ½ AB [D is the midpoint of AB]

AD = ½ ×9 = 9/2

⇒ AE = ½ AC [E is the midpoint of AC]

⇒ AE = ½ ×15 = 15/2

ADE is a right triangle.

⇒ (15/2)² = (9/2)²+DE²

⇒ DE² = (15/2)² – (9/2)²

⇒ DE² = 225/4 -81/4

⇒ DE² = 144/4

Taking square root on both sides,

DE = 12/2 = 6 cm.

Area of ADE = ½ ×DE×AD

= ½ ×6×9/2

= 13.5 cm²

Therefore, the area of the ADE is 13.5 cm².

Question 2. If in ∆ ABC, AB > AC and DI BC, prove that AB² – AC² = BD² – CD².

Answer : Given AD BC, AB>AC

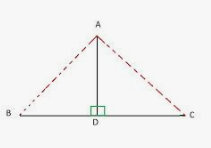
So ADB and ADC are right triangles.

Proof:

In ADB,

⇒ AD² = AB²-BD² …(i)

In ADC,

AC² = AD²+CD²

⇒ AD² = AC²-CD² …(ii)

Equating (i) and (ii)

AB²-BD² = AC²-CD²

AB²-AC² = BD²– CD²

Hence proved.

Question 3.  In a right angled triangle ABC, right angled at C, P and Q are the points on the sides CA and CB respectively which divide these sides in the ratio 2:1. Prove that

(i) 9AQ² = 9AC² + 4BC²
(ii) 9BP² = 9BC² + 4AC²
(iii) 9(AQ² + BP²) = 13AB².

Answer : Join AQ and BP,   Given C = 90°

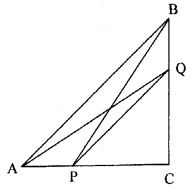
Proof:  (i) In ACQ,

Multiplying both sides by 9

9AQ² = 9AC²+9CQ²

⇒ 9AQ² = 9AC²+(3CQ)² …(i)

Given BQ: CQ = 1:2

⇒ CQ/BC = CQ/(BQ+CQ)

⇒ CQ/BC = 2/3

⇒ 3CQ = 2BC …(ii)

Substitute (ii) in (i)

9AQ² = 9AC²+(2BC)²

⇒ 9AQ² = 9AC²+4BC² …(iii)

Hence, proved.

(ii) In BPC,

Multiplying both sides by 9, we get

9BP² = 9BC²+9CP²

⇒ 9BP² = 9BC²+(3CP)² …(iv)

Given AP: PC = 1:2

CP/AC = CP/AP+PC

⇒ CP/AC = 2/3

⇒ 3CP = 2AC …(v)

Substitute (v) in (iv)

9BP² = 9BC²+(2AC)²

⇒ 9BP² = 9BC²+4AC² …(vi)

Hence proved.

(iii) Adding (iii) and (vi), we get

9AQ²+9BP² = 9AC²+4BC²+9BC²+4AC²

⇒ 9(AQ²+BP)² = 13AC²+13BC²

⇒ 9(AQ²+BP)² = 13(AC²+BC²) …(vii)

In ABC,

AB² = AC²+BC² …(viii)

Substitute (viii) in (viii), we get

9(AQ²+BP)² = 13AB²

Hence proved.

Question 4. In the given figure, ∆PQR is right angled at Q and points S and T trisect side QR. Prove that 8PT² – 3PR² + 5PS².

Answer : Q = 90° given

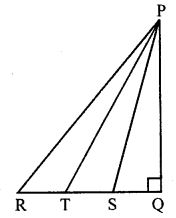
S and T are points on RQ such that these points trisect it.

So RT = TS = SQ

To prove : 8PT² = 3PR² + 5PS².

Proof:

Let RT = TS = SQ = x

In PRQ,

⇒ PR² = (3x)²+PQ²

⇒ PR² = 9x²+PQ²

Multiply above equation by 3

3PR² = 27x²+3PQ² …(i)

Similarly in PTS,

⇒ PT² = (2x)²+PQ²

⇒ PT² = 4x²+PQ²

Multiply above equation by 8

8PT² = 32x²+8PQ² …(ii)

Similarly in PSQ,

⇒ PS² = x²+PQ²

Multiply above equation by 5

5PS² = 5x²+5PQ² …(iii)

Add (i) and (iii), we get

3PR² +5PS² = 27x²+3PQ²+5x²+5PQ²

⇒ 3PR² +5PS² = 32x²+8PQ²

⇒ 3PR² +5PS² = 8PT² [From (ii)]

8PT² = 3PR² +5PS²

Hence proved.

Question 5. In a quadrilateral ABCD, ∠B = 90°. If AD² = AB² + BC² + CD², prove that ∠ACD = 90°.

Answer :

B = 90˚ in quadrilateral ABCD

AD² = AB² + BC² + CD²

To prove: ACD = 90°

Proof:  In ABC,

AC² = AB²+BC² …(i) 

Given,   AD² = AB² + BC² + CD²

⇒ AD² = AC²+CD² [from (i)]

In ACD, ACD = 90° [Converse of Pythagoras theorem]

Hence proved.

Question 6.  In the adjoining figure, find the length of AD in terms of b and c.

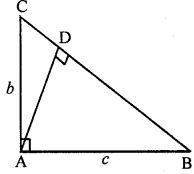
Answer : given  A = 90° , AB = c , AC = b

ADB = 90°

In ABC,

⇒ BC² = b²+c²

⇒ BC = √( b²+c²) …(i)

Area of ABC = ½ ×AB×AC

= ½ ×bc …(ii)

Also, Area of ABC = ½ ×BC×AD

= ½ ×√( b²+c²) ×AD …(iii)

Equating (ii) and (iii)

½ ×bc = ½ ×√( b²+c²) ×AD

⇒ AD = bc /(√( b²+c²)

Therefore,

AD is bc /(√( b²+c²).

Question 7. ABCD is a square, F is mid-point of AB and BE is one-third of BC. If area of ∆FBE is 108 cm², find the length of AC.

Answer :  Let x be each side of the square ABCD.

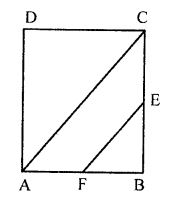
FB = ½ AB [∵ F is the midpoint of AB]

FB = ½ x …(i)

BE = (1/3) BC

⇒ BE = (1/3) x …(ii)

AC = √2 ×side

⇒ AC = √2x

Area of FBE = ½ FB×BE

108 = ½ × ½ x ×(1/3)x [given area of FBE = 108 cm²]

⇒ 108 = (1/12)x²

⇒ x² = 108×12

⇒ x² = 1296

Taking square root on both sides.

x = 36

AC = √2×36 = 36√2

Therefore,

length of AC is 36√2 cm.

Question 8. In a triangle ABC, AB = AC and D is a point on side AC such that BC² = AC x CD, Prove that BD = BC.

Answer :   In ABC, AB = AC

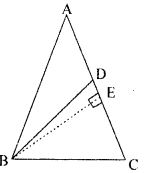
D is a point on side AC such that BC² = AC×CD

To prove :  BD = BC

Construction:   Draw BEAC

Proof:   In BCE ,

⇒ BC² = BE²+(AC-AE)²

⇒ BC² = BE²+AC²+AE²– 2 AC×AE

⇒ BC² = BE²+AE²+AC²– 2 AC×AE …(i)

In ABC,

AB² = BE²+AE² …(ii)

Substitute (ii) in (i)

BC² = AB²+AC²– 2 AC×AE

⇒ BC² = AC²+AC²– 2 AC×AE [∵AB = AC]

⇒ BC² = 2AC²-2 AC×AE

⇒ BC² = 2AC(AC-AE)

⇒ BC² = 2AC×EC

BC² = AC × CD

⇒ 2AC×EC = AC × CD

⇒ 2EC = CD …(ii)

E is the midpoint of CD.

EC = DE …(iii)

In BED and BEC,

EC = DE [From (iii)]

BE = BE [common side]

BED = BEC [By SAS congruency rule]

BD = BD [c.p.c.t]

Hence proved.

—  : End of ML Aggarwal Pythagoras Theorem Chapter Test Class 9 ICSE Maths Solutions :–

Return to :-   ML Aggarawal Maths Solutions for ICSE  Class-9

Thanks

Please Share with Your Friends