ML Aggarwal Section Formula Chapter-Test Solutions ICSE Class-10 Maths Ch-11

ML Aggarwal Section Formula Chapter-Test Solutions ICSE Class-10 Maths Ch-11. We Provide Step by Step Answer of Exercise-11 Section Formula Chapter-Test Questions. Visit official Website CISCE for detail information about ICSE Board Class-10.

ML Aggarwal Section Formula Chapter-Test Solutions ICSE Class-10 Maths Ch-11

Board	ICSE
Publications	Avichal Publishig Company (APC)
Subject	Maths
Class	10th
Chapter-11	Section Formula
Writer	ML Aggarwal
Book Name	Understanding
Topics	Solution of Chapter Test Questions
Edition	2022-2023

ML Aggarwal Section Formula Chapter-Test Solutions ICSE Class-10 Maths Ch-11

Page-225

Question-1 The base BC of an equilateral triangle ABC lies on y-axis. The coordinates of the point C are (0, – 3). If origin is the mid-point of the base BC, find the coordinates of the points A and B

Answer- 1

Base BC of an equilateral ∆ABC lies on y-axis
co-ordinates of point C are (0, – 3),
origin (0, 0) is the mid-point of BC.

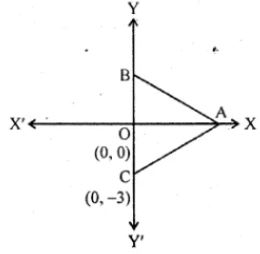
Let co-ordinates of B be (x, y)

∴ 0 = (x + 0)/2

⇒ x/2 = 0

⇒ x = 0

(y – 3)/2 = 0

⇒ y – 3 = 0

⇒ y = 3

∴ Co-ordinates of B are (0, 3)

Again let co-ordinates of A be (x, 0) as it lies on x-axis.

∵ AB = AC = BC = 6 units

x² + (- 3)² = 6²

x² + 9 = 36

⇒ x² = 36 – 9 = 27

⇒ x = ± 3√3

∴ Co-ordinates of A will be (±3√3, 0)

Question -2 Find the co-ordinates of the point that divides the line segment joining the points P (5, – 2) and Q (9, 6) internally in the ratio of 3 : 1.

Answer -2

Let R be the point whose co-ordinates are (x, y)
which divides PQ in the ratio of 3:1.

∴ x = (m₁x₂ + m₂x₁)/(m₁ + m₂)

= (3×9 + 1×5)/(3 + 1)

= (27+5) / 4,  = 32/4,  = 8

y = (m₁y₂ + m₂y₁)/(m₁ + m₂)

= {3×6 + 1×(-2)}/(3+1)

= (18–2) / 4

= 16/4,  = 4

∴ Co-ordinates of R will be (8, 4)

Question -3  Find the coordinates of the point P which is three-fourth of the way from A (3, 1) to B ( – 2, 5).

Answer-3

Co-ordinates of A (3, 1) and B ( – 2, 5)
P lies on AB such that

AP = 3/4 AB = 3/4 (AP + PB)

⇒ AP = 3PB

⇒ AP : PB = 3 : 1

Let co-ordinates of P be (x, y)

∴ x = (mx₂ + nx₁)/(m + n) = {(3 × (-2) + 1 × 3}/(3 + 1)

= (-6 + 3)/4

= -3/4

y = (my₂ + ny₁)/(m + n)

= (3×5 + 1×1)/(3+1)

= (15+1) / 4

= 16/4,  = 4

∴ Co-ordinates of Pare (-3/4, 4)

Question -4  P and Q are the points on the line segment joining the points A (3, – 1) and B ( – 6, 5) such that AP = PQ = QB. Find the co-ordinates of P and Q.

Answer-4

Given

AP = PQ = QB

∴ P divides AB in the ratio of 1 : 2 and Q divides it in 2 : 1.

Let co-ordinates of P will be (x₁, y₁) and of Q will (x₂, y₂)

∴ x₁ = (m₁x₂ + m₂x₁)/(m₁ + m₂)

= {1×(-6) + 2×3}/(1+2)

= (- 6 + 6)/3

= 0/3

= 0

y₁ = (m₁y₂ + m₂y₁)/(m₁ + m₂)

= {1×5 + 2(-1)}/(1+2)

= (5-2)/3

= 3/3   = 1

∴ Co-ordinates of P will be (0, 1)

Again

x₂ = (m₁x₂ + m₂x₁)/(m₁ + m₂)

= {2×(-6) + 1×3}/(2+1)

= (-12+3)/3

= -9/3,  = – 3

y₂ = (m₁y₂ + m₂y₁)/(m₁ + m₂)

= {2×5 + 1×(-1)}/(2+1)

= (10–1)/3

= 9/3 ,  = 3

∴ Co-ordinates of Q will be (-3, 3).

Question-5  The centre of a circle is (α + 2, α – 5). Find the value of a given that the circle passes through the points (2, – 2) and (8, – 2).

Answer -5

Let A (2, -2), B (8, -2) and centre of the circle be
O (α + 2, α – 5)

Squaring both sides,

𝝰² + (𝝰 + 1)² = (6 – 𝝰)² = (1 + a)²

⇒ a² = (6 – 𝝰)² [dividing by (𝝰 + 1)²]

⇒ 𝝰² = 36 – 12𝝰 + 𝝰²

= 𝝰² – 𝝰² + 12𝝰

= 36

⇒ 12𝝰 = 36

∴ = 36/12 = 3

---

ML Aggarwal Section Formula Chapter-Test Solutions ICSE Class-10 Maths

Question -6 The mid-point of the line joining A (2, p) and B (q, 4) is (3, 5). Calculate the numerical values of p and q.

Answer -6

Given
(3, 5) is the mid-point of A (2, p) and B (q, 4)

∴ 3 = (2 + q)/2

⇒ 2 + q = 6

⇒ q = 6 – 2 = 4

∴ q = 4

And 5 = (p + 4)/2

⇒ p + 4 = 10

⇒ p = 10 – 4 = 6

∴ p = 6

Hence,

p = 6, q = 4

Question-7 The ends of a diameter of a circle have the co-ordinates (3, 0) and ( – 5, 6). PQ is another diameter where Q has the coordinates ( – 1, – 2). Find the co-ordinates of P and the radius of the circle.

Answer -7

Let AB be the diameter where co-ordinates of
A are (3, 0) and of B are (-5, 6).
Co-ordinates of its origin O will be

{(3 – 5)/2, (0 + 6)/2} or (-2/2, 6/2) or (- 1, 3)

Now PQ is another diameter in which co-ordinates of Q are (-1, -2).

Let co-ordinates of P be (x, y)

Then co-ordinates of center O will be {(- 1 + x)/2, (-2 + y)/2}

∴ (-1+x)/2 = – 1

⇒ – 1+x = – 2

⇒ x = -2 + 1 = – 1

And (- 2 + y)/2 = 3

⇒ – 2 + y = 6

⇒ y = 6 + 2 = 8

∴ Co-ordinates of P will be (-1, 8)

Question -8 In what ratio does the point ( – 4, 6) divide the line segment joining the points A( – 6, 10) and B (3, – 8) ?

Answer -8

Let the point (-4, 6) divides the line segment joining the points
A (-6, 10) and B (3, -8), in the ratio m : n

∴ – 4 = (mx₂ + nx₁)/(m + n) = {m × 3 + n(-6)}/(m + n)

– 4 = (3m – 6n)/(m + n)

⇒ – 4m – 4n = 3m – 6n

⇒ – 4n + 6n = 3m + 4m

⇒ 7m = 2n

⇒ m/n = 2/7

∴ Ratio = 2 : 7

Question -9   Find the ratio in which the point P ( – 3, p) divides the line segment joining the points ( – 5, – 4) and ( – 2, 3). Hence find the value of p.

Answer -9

Let P (-3, p) divides AB in the ratio of m₁ : m₂ coordinates of
A (-5, -4) and B (-2, 3)

∴ – 3 = (m₁x₂ + m₂x₁)/(m₁ + m₂)

⇒ – 3 {m₁(-2) + m₂(-5)}/(m₁ + m₂)

⇒ – 3 = (- 2m₁ – 5m₂)/(m₁ + m₂)

⇒ – 3m₁ – 3m₂ = – 2m₁ – 5m₂

⇒ – 3m₁ + 2m₁ = – 5m₂ + 3m₂

⇒ – m₁ = – 2m₂

⇒ 2m₂ = m₁

⇒ m₁/m₂ = 2/1

⇒ m₁: m₂ = 2 : 1

Again,

p = (m₁y₂ + m₂y₁)/(m₁ + m₂)

= {(2×3 + 1×(-4)}/(2 + 1)

= (6 – 4)/3

= 2/3

Hence,

p = 2/3

Question -10  In what ratio is the line joining the points (4, 2) and (3, – 5) divided by the x-axis? Also find the co-ordinates of the point of division.

Answer-10

Let the point P which is on the x-axis, divides the line segment
joining the points A (4, 2) and B (3, -5) in the ratio of m₁ : m₂.
and let co-ordinates of P be (x, 0)

∴ 0 = (m₁y₂ + m₂y₁)/(m₁ + m₂)

= {m₁(-5) + m₂(2)}/(m₁ + m₂)

⇒ (- 5m₁ + 2m₂)/(m₁ + m₂) = 0

⇒ – 5m₁ + 2m₂ = 0

⇒ – 5m₁ = – 2m₂

⇒ 5m₁ = 2m₂

⇒ m₁/m₂ = 2/5

⇒ m₁ : m₂ = 2 : 5

x = (m₁x₂ + m₂x₁)/(m₁ + m₂)

= {2×3 + 5×4}/(2+5)

= (6 + 20)/7

= 26/7

∴ Co-ordinates of P will be (26/7, 0)

---

ML Aggarwal Section Formula Chapter-Test Solutions ICSE Class-10 Maths

Question -11 If the abscissa of a point P is 2, find the ratio in which it divides the line segment joining the points ( – 4 – 3) and (6, 3). Hence, find the co-ordinates of P.

Answer -11

Let co-ordinates of A be (-4, 3) and of B (6, 3) and of P be (2, y)
Let the ratio in which the P divides AB be m₁ : m₂

∵ x = (m₁x₂ + m₂x₁)/(m₁ + m₂)

⇒ 2 = (m₁×6 + m₂×(-4)}/(m₁+m₂)

⇒ 2 = (6m₁ – 4m₂)/(m₁ + m₂)

⇒ 2m₁ + 2m₂ = 6m₁ – 4m₂

⇒ 6m₁ – 2m₁ = 2m₂ + 4m₂

⇒ 4m₁ = 6m₂

⇒ m₁/m₂ = 6/4 = 3/2

∴ m₁ : m₂ = 3 : 2

∴ y = (m₁y₂ + m₂y₁)/(m₁+m₂)

= (3×3 + 2×3)/(3+2)

= (9 + 6)/5

= 15/5

= 3

∴ Co-ordinates of P will be (-2, 3)

Question- 12  Determine the ratio in which the line 2x + y – 4 = 0 divide the line segment joining the points A (2, – 2) and B (3, 7). Also find the co-ordinates of the point of division.

Answer -12

Points are given A (2, -2), B (3, 7)
and let the line 2x + y – 4 = 0 divides AB in the ratio m₁ : m₂
at P and let co-ordinates of

x = (m₁x₂ + m₂x₁)/(m₁ + m₂)

= (m₁×3 + m₂×2 )/ (m₁ + m₂)

= (3m₁ + 2m₂)/(m₁ + m₂)

And y = {m₁×7 + m₂×(-2)}/(m₁+m₂)

= {7m₁ – 2m₂}/(m₁+m₂)

∴ P lies on the line 2x + y – 4 = 0, then

2(3m₁ + 2m₂)/(m₁+m₂) + (7m₁ – 2m₂)/(m₁+m₂) – 4 = 0

⇒ 6m₁ + 4m₂ + 7m₁ – 2m₂ – 4m₁ – 4m₂ = 0

⇒ 9m₁ – 2m₂ = 0

⇒ 9m₁ = 2m₂

⇒ m₁/m₂ = 2/9

or m₁ : m₂ = 2 : 9

∴ x = (2×3 + 2×9)/(2 + 9)

= (6 + 18)/11

= 24/11

And y = (2 × 7 – 2 × 9)/(2 + 9)

= (14 – 18)/11

= -4/11

∴ Co-ordinates of P will be (24/11, -4/11)

Question -13 ABCD is a parallelogram. If the coordinates of A, B and D are (10, – 6), (2, – 6) and (4, – 2) respectively, find the co-ordinates of C.

Answer-13

Let the co-ordinates of C be (x, y) and other three vertices
of the given parallelogram are A (10, – 6), B, (2, – 6) and D (4, – 2)
∴ ABCD is a parallelogram
Its diagonals bisect each other.
Let AC and BD intersect each other at O.
∴O is mid-points of BD
∴ Co-ordinates of O will be

{(2+4)/2, (-6–2)/2) or (6/2, -8/2) or (3, -4)

Again, O is the mid-point of AC then

3 = (10 + x)/2

⇒ 10 + x = 6

⇒ x = 6 – 10 = – 4

And – 4 = (-6 + y)/2

⇒ 6 + y = – 8

⇒ – 8 + 6

∴ y = – 2

Hence Co-ordinates of C will be (- 4, – 2).

---

Section Formula Chapter-Test

ML Aggarwal Solutions ICSE Class-10 Maths

Page-226

Question -14  

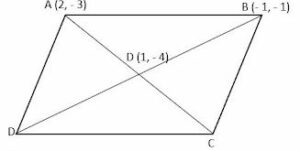
ABCD is a parallelogram whose vertices A and B have co-ordinates (2, – 3) and ( – 1, – 1) respectively. If the diagonals of the parallelogram meet at the point M(1, – 4), find the co-ordinates of C and D. Hence, find the perimeter of the parallelogram. find the perimeter of the parallelogram.

Answer -14

ABCD is a || gm , m which co-ordinates of A are (2, -3) and B (-1, -1)
Its diagonals AC and BD bisect each other at M (1, -4)
∴ M is the midpoint of AC and BD
Let co-ordinates of C be (x₁, y₁) and of D be (x₂, y₂)
when M is the midpoint of AC then

∴ l = (2 + x₁)/2 and – 4 = (-3 + y₁)/2

⇒ 2 + x₁ = 2

⇒ x₁ = 2 – 2 = 0

And –8 = -3 + y₁

⇒ y₁ = -8 + 3 = -5

∴ Co-ordinates of C are (0, -5)

Again M is mid-point of BD, then

1 = (-1 + x₂)/2, -4 = (-1 + y₂)/2

⇒ -1 + x₂ = 2

⇒ x₂ = 2 + 1 = 3

And –1 + y₂ = -8

⇒ y₂ = -8 + 1 = -7

∴ Co-ordinates of D are (3, -7)

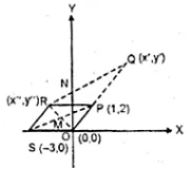
Question -15  Given, O, (0, 0), P(1, 2), S( – 3, 0) P divides OQ in the ratio of 2 : 3 and OPRS is a parallelogram.
Find : 

(i) the co-ordinates of Q.
(ii)the co-ordinates of R.
(iii) the ratio in which RQ is divided by y-axis.

Answer -15

(i) Let co-ordinates of Q be (x’, y’) and of R (x”, y”) Point P (1, 2) divides OQ in the ratio of 2 : 3

∴ l = (m₁x₂ + m₂x₁)/(m₁ + m₂)

= (2x’ + 3×0)/(2+3)

⇒ (2x’+0)/5 = 1

⇒ 2x’ = 5

⇒ x’ = 5/2

And 2 = (m₁y₂ + m₂y₁)/(m₁+m₂)

= (2y’ + 3×0)/(2+3)

⇒ 2y’/5 = 2

⇒ 2y’ = 10

⇒ y’ = 5

∴ Co-ordinates of Q will be (5/2, 5)

∵ the diagonals of a parallelogram bisect each other

∴ In ||gm OPRS, diagonals OR and PS bisect each other at M.

∵ M is the mid-point of PS

∴ Co-ordinates of M will be = {(-2+1)/2, (0+2)/2}

or (-2/2, 2/2)

or (-1, 1)

(ii) ∵ M is the mid-point of OR also

∴ – 1 = (0 + x’’)/2

⇒ x’’ = – 2

And 1 = (0 + y’’)/2

⇒ y’’ = – 2

∴ Co-ordinates of R will be (- 2, 2)

(iii) RQ is dividing by y-axis in N

Let the ratio in which N divides RQ in m₁ : m₂

∵ N lies on y-axis

∴ its abscissa (x) = 0

0 = (m₂x’ + m₂x”)/(m₁ + m₂)

⇒ 0 = {m₁×5/2 + m₂×(-2)}/(m₁+m₂)

⇒ (5m₁/2 – 2m₂)/(m₁+m₂) = 0

⇒ 5/2 m₁ – 2m₂ = 0

⇒ 5/2 m₁ = 2m₂

⇒ m₁/m₂ = (2×2)/5 = 4/5

∴ m₁ : m₂ = 4 : 5

Question -16  If A (5, – 1), B ( – 3, – 2) and C ( – 1, 8) are the vertices of a triangle ABC, find the length of the median through A and the co-ordinates of the centroid of triangle ABC.

Answer -16

A (5, -1), B (-3, -2) and C (-1, 8) are the vertices of ∆ABC
D, E and F are the midpoints of sides BC, CA and AB respectively
and G is the centroid of the ∆ABC

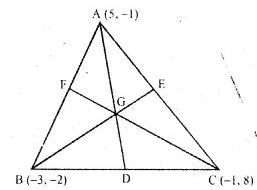
∵ D is the midpoint of BC

∴ Co-ordinates of D will be {(x₁ + x₂)/2}, (y₁ + y₂)/2} or {(-3 –1)/2 , (-2+8)/2} or (-4/2, 6/2) or (-2, 3)

∵ G is the centroid

∴ Co-ordinates of G will be {(x₁ + x₂ + x₃)/3 , (y₁ + y₂ + y₃)/3}

Or {(5 – 3 – 1)/3, (-1–2 + 8)/3} or (1/3, 5/3)

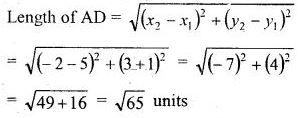
–: ML Aggarwal Section Formula Chapter-Test Solutions ICSE Class-10 Maths:–