ML Aggarwal Statistics Chapter Test Class 9 ICSE Maths APC Understanding Solutions. Solutions of Chapter Test . This post is the Solutions of ML Aggarwal Chapter 20 – Statistics for ICSE Maths Class-9. APC Understanding ML Aggarwal Solutions (APC) Avichal Publication Solutions of Chapter – 20 Statistics for ICSE Board Class-9. Visit official website CISCE for detail information about ICSE Board Class-9.
ML Aggarwal Statistics Chapter Test Class 9 ICSE Maths Solutions
| Board | ICSE |
| Publications | Avichal Publishig Company (APC) |
| Subject | Maths |
| Class | 9th |
| Chapter-20 | Statistics |
| Writer | ML Aggarwal |
| Book Name | Understanding |
| Topics | Solution of Chapter Test Questions |
| Edition | 2021-2022 |
Chapter Test Solutions of ML Aggarwal for ICSE Class-9 Ch-20, Statistics
Note:- Before viewing Solutions of Chapter – 20 Statistics Class-9 of ML Aggarwal Solutions . Read the Chapter Carefully. Then solve all example given in Exercise-20.1, Exercise-20.2, Exercise-20.3, MCQs, Chapter Test.
Statistics Chapter Test
ML Aggarwal Class 9 ICSE Maths Solutions
Page 500
Question 1. Find the mean and the median of the following set of numbers:
8, 0, 5, 3, 2, 9, 1, 5, 4, 7, 2, 5.
Answer :
In descending order
0, 1, 2, 2, 3, 4, 5, 5, 5, 7, 8, 9
n = 12 which is even
Mean (x̄) = Ʃ xi/n
= (0 + 1 + 2 + 2 + 3 + 4 + 5 + 5 + 5 + 7 + 8 + 9)/12
= 51/12
= 17/4
= 4.25
Median = ½ [12/2th + (12/2 + 1)th terms]
= ½ [6th + 7th terms]
= ½ (4 + 5)
= 9/2
= 4.5
Question 2. Find the mean and the median of all the (positive) factors of 48.
Answer :
Positive factors of 48 are
1, 2, 3, 4, 6, 8, 12, 16, 24, 48
Here N = 10 which is even
Mean (x̄) = Ʃ xi/ n
= (1 + 2 + 3 + 4 + 6 + 8 + 12 + 16 + 24 + 48)/10
= 124/10
= 12.4
Median = ½ [10/2 th + (10/2 + 1)th terms]
= ½ [5th + 6th terms]
= ½ (6 + 8)
= 14/2
= 7
Question 3. The mean weight of 60 students of a class is 52.75 kg. If the mean weight of 35 of them is 54 kg, find the mean weight of the remaining students.
Answer :
Mean weight of 60 students of a class=52.75 kg
So the total weight of 60 students = 52.75 × 60
= 3165 kg
Mean weight of 35 students among them = 54 kg
So the total weight of 35 students = 54 × 35
= 1890 kg
Remaining students = 60 – 35
= 25
Total weight of 25 students = 3165 – 1890
= 1275 kg
So the mean weight of 25 students = 1275 ÷ 25
= 51 kg
Hence, the mean weight of the remaining students is 51 kg.
Question 4. The mean age of 18 students of a class is 14.5 years. Two more students of age 15 years and 16 years join the class. What is the new mean age?
Answer :
Mean age of 18 students = 14.5 years
Total age = 14.5 × 18
= 261 years
Total age of 2 more students = 15 + 16
= 31 years
Total age of 18 + 2 = 20 students = 261 + 31
= 292 years
Mean age = 292/20 =
14.6 years
Hence, the new mean age is 14.6 years.
Question 5. If the mean of the five observations x + 1, x + 3, x + 5, 2x + 2, 3x + 3 is 14, find the mean of first three observations.
Answer :
Mean of the five observations
x + 1, x + 3, x + 5, 2x + 2, 3x + 3 is 14
Mean = (x + 1 + x + 3 + x + 5 + 2x + 2 + 3x + 3)/5
= (8x + 14)/5
(8x + 14)/5 =14
8x + 14 = 70
8x = 70 – 14 = 56
x = 56/8 = 7
Mean of x + 1 + x + 3 + x + 5
Mean = (x + 1 + x + 3 + x + 5)/3
= (3x + 9)/3
= x + 3
Substituting the value of x
= 7 + 3
= 10
Therfore, the mean of first three observations is 10.
Question 6. The mean height of 36 students of a class is 150.5 cm. Later on, it was detected that the height of one student was wrongly copied as 165 cm instead of 156 cm. Find the correct mean height.
Answer :
Mean height of 36 students of a class=150.5 cm
Total height = 150.5 × 36
= 5418 cm
Difference in height which was wrongly copied = 165 + 56
= 9 cm
Actual height = 5418 – 9
= 5409 cm
Actual mean height = 5409/36
= 150.25 cm
Therfore, the correct mean height is 150.25 cm.
Question 7. The mean of 40 items is 35. Later on, it was discovered that two items were misread as 36 and 29 instead of 63 and 22. Find the correct mean.
Answer :
Mean of 40 items = 35
Total of 40 items = 35 × 40 = 1400
Difference between two items which were wrongly read = (63 + 22) – (36 + 29)
= 85 – 65
= 20
Here,
Actual total = 1400 + 20 = 1420
Correct mean = 1420/40 = 35.5
Therefore, the correct mean is 35.5.
Question 8. The following observations have been arranged in ascending order. If the median of the data is 63, find the value of x.
29, 32, 48, 50, x, x + 2, 72, 75, 87, 91.
Answer :
N = 10 which is even
Median = ½ [n/2 th + (n/2 + 1)th term]
63 = ½ [10/2th + (10/2 + 1)th term]
63 = ½ (5th + 6th terms)
63 = ½ (x + x + 2)
63 × 2 = 2x + 2
2x = 126 – 2 = 124
By division
x = 124/2 = 62
Hence, the value of x is 62.
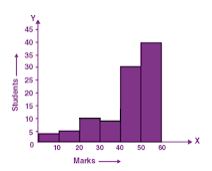
Question 9. Draw a histogram showing marks obtained by the students of a school in a Mathematics paper carrying 60 marks.
| Marks | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 | 50-60 |
| Students | 4 | 5 | 10 | 8 | 30 | 40 |
Answer :
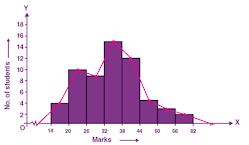
Question 10. In a class of 60 students, the marks obtained in a surprise test were as under:
| Marks | 14-20 | 20-26 | 26-32 | 32-38 | 38-44 | 44-50 | 50-56 | 56-62 |
| No. of students | 4 | 10 | 9 | 15 | 12 | 5 | 3 | 2 |
Answer :
Question 11. Construct a combined histogram and frequency polygon for the following distribution:
| Classes | 91-100 | 101-110 | 111-120 | 121-130 | 131-140 | 141-150 | 151-160 |
| Frequency | 16 | 28 | 44 | 20 | 32 | 12 | 4 |
Answer :
the classes in continuous frequency classes:
| Classes | Classes after adjustment | Frequency |
| 91-100 | 90.5-100.5 | 16 |
| 101-110 | 100.5-110.5 | 28 |
| 111-120 | 110.5-120.5 | 44 |
| 121-130 | 120.5-130.5 | 20 |
| 131-140 | 130.5-140.5 | 32 |
| 141-150 | 140.5-150.5 | 12 |
| 151-160 | 150.5-160.5 | 4 |
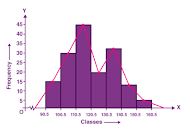
Question 12. The electricity bills (in rupees) of 40 houses in a locality are given below:
78 87 81 52 59 65 101 108 115 95
98 65 62 121 128 63 76 84 89 91
65 101 95 81 87 105 129 92 75 105
78 72 107 116 127 100 80 82 61 118
Form a frequency distribution table with a class size of 10. Also represent the above data with a histogram and frequency polygon.
Answer :
Least term = 52
Greatest term = 129
Range = 129 – 52 = 77
| Class Interval | Tally Numbers | Frequency |
| 50-60 | II | 2 |
| 60-70 | 6 | |
| 70-80 | 5 | |
| 80-90 | 8 | |
| 90-100 | 5 | |
| 100-110 | 7 | |
| 110-120 | III | 3 |
| 120-130 | IIII | 4 |
| Total | 40 |
Statistics Chapter Test
ML Aggarwal Class 9 ICSE Maths Solutions
Page 501
Question 13. The data given below represent the marks obtained by 35 students:
21 26 21 20 23 24 22 19 24
26 25 23 26 29 21 24 19 25
26 25 22 23 23 27 26 24 25
30 25 23 28 28 24 28 28
Taking class intervals 19-20, 21-22 etc., make a frequency distribution for the above data.
Construct a combined histogram and frequency polygon for the distribution.
Answer :
Least mark = 19
Greatest marks = 30
Range = 30 – 19 = 11
| Class Interval | Actual Intervals | Frequency |
| 19-20 | 18.5-20.5 | 3 |
| 21-22 | 20.5-22.5 | 5 |
| 23-24 | 22.5-24.5 | 10 |
| 25-26 | 24.5-26.5 | 10 |
| 27-28 | 26.5-28.5 | 5 |
| 29-30 | 28.5-30.5 | 2 |
| Total | 35 |

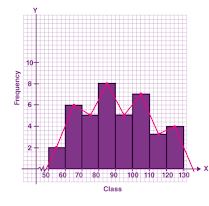
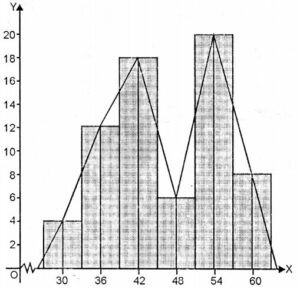
Question 14. The given histogram and frequency polygon shows the ages of teachers in a school. Answer the following:
(i) What is the class size of each class?
(ii) What is the class whose class mark is 48?
(iii) What is the class whose frequency is maximum?
(iv) Construct a frequency table for the given distribution.
Answer :
(i) The class size of each class is 6.
(ii) The class whose class mark is 48 is 45 – 51
= (45 + 51)/2
= 96/2
= 48
(iii) The class 51-57 has the maximum frequency i.e., 20.
(iv) Frequency table for the given distribution:
| Classes | 27-33 | 33-39 | 39-45 | 45-51 | 51-57 | 57-63 |
| Frequency | 4 | 12 | 18 | 6 | 20 | 8 |
— : End of ML Aggarwal Statistics Chapter Test Class 9 ICSE Maths Solutions :–
Return to :- ML Aggarawal Maths Solutions for ICSE Class-9
Thanks
Please Share with Your Friend