Circle Circumference and Area Class 9 OP Malhotra Exe-17A ICSE Maths Solutions Ch-17. We Provide Step by Step Solutions / Answer of Area of Trapezium for OP Malhotra Maths. Visit official Website CISCE for detail information about ICSE Board Class-9 Mathematics.

Circle Circumference and Area Class 9 OP Malhotra Exe-17A ICSE Maths Solutions Ch-17
| Board | ICSE |
| Publications | S Chand |
| Subject | Maths |
| Class | 9th |
| Chapter-17 | Circle Circumference and Area |
| Writer | OP Malhotra |
| Exe-17A | Solved Questions on Circumference of Circle |
| Edition | 2025-2026 |
Solved Questions on Circumference of Circle
Circle Circumference and Area Class 9 OP Malhotra Exe-17A ICSE Maths Solutions Ch-17
Take π = 22/7 unless stated otherwise.
Que-1: Find the circumference of the circles whose diameters are :
(i) 49 cm
(ii) 14 cm
(iii) 9.8 cm
(iv) 7 cm
Sol: (i) Diameter of the circle (d) = 49 cm
∴ Circumference = πd = (22/7) × 49 = 154 cm
(ii) Diameter of the circle (d) = 14 cm
∴ Circumference = πd = (22/7) × 14 = 44 cm
(iii) Diameter of the circle (d) = 9.8 cm
∴ Circumference = πd = (22/7) × 9.8 = 30.8 cm
(iv) Diameter of the circle (d) = 7 cm
∴ Circumference = πd = (22/7) × 7 = 22 cm
Que-2: Find the circumference of the circles whose radii are :
(i) 7 cm
(ii) 28 cm
(iii) 3.5 cm
(iv) 98 m
Sol: (i) Radius of the circle (r) = 7 cm
∴ Circumference = 2 πr = 2 × (22/7) × 7 = 44 cm
(ii) Radius of the circle (r) = 28 cm
∴ Circumference = 2 πr = 2 × (22/7) × 28 = 176 cm
(iii) Radius of the circle (r) = 3.5 cm
∴ Circumference = 2 πr = 2 × (22/7) × 3.5 = 22 cm
(iv) Radius of the circle (r) = 98 m
∴ Circumference = 2 πr = 2 × (22/7) × 98 = 616 cm
Que-3: Find the circumference of the circles, if
(i) Radius = 4.5 cm
(ii) Diameter = 15 cm (Take π = 3.14 in (i) and (ii) above.)
Sol: (i) Radius (r) = 4.5 cm
∴ Circumference = 2 πr = 2 × 3.14 × 4.5 = 28.26 cm = 28.3 cm
(ii) Diameter (d) = 15 cm
∴ Circumference = πd = 3.14 × 15 × cm = 47.10 = 47.1 cm
Que-4: Find the length of the diameter of the circles whose circumference are :
(i) 22 cm
(ii) 8.8 cm
(iii) 44 cm
Sol: (i) Circumference = 22 cm
Let d be the diameter of the circle
∴ d = circumference π = {22/(22/7)} = (22×7)/22 = 7 cm
∴ Diameter = 7 cm
(ii) Circumference = 8.8 cm
∴ Diameter = circumference π = {8.8/(22/7)} = (8.8×7)/22 = 0.4 × 7 = 2.8 cm
(iii) Circumference = 44 cm
∴ Diameter = circumference π = {44/(22/7)} = (44×7)/22 = 14 cm
Que-5: Find the lengths of the radii of the circles whose circumferences are
(i) 11 cm
(ii) 55 cm
(iii) 13.2 m
(iv) 440 m
Sol: (i) Circumference = 11 cm
Let radius of the circle = r
Then 2πr = 11
⇒ 2×(22/7)r = 11 ⇒ r = (11×7)/(2×22) = 7/4
∴ Radius = 7/4 cm = 1.75 cm
(ii) Circumference = 55 cm
Let radius of the circle = r
Then 2πr = 55
⇒ 2×(22/7)r = 55 ⇒ r = (55×7)/2×22
⇒ r = 35/4 = 8.75
∴ Radius = 8.75 cm
(iii) Circumference = 13.2 cm
Let radius of the circle = r
Then 2πr = 13.2 m
⇒ 2×(22/7)r = 13.2 ⇒ r = (13.2×7)/(2×22) = 21/10 = 2.1
∴ Radius = 2.1 cm
(iv) Circumference = 440 m
Let radius of the circle = r
Then 2πr = 440
⇒ 2×(22/7)r = 440 ⇒ r = (440×7)/2×22 ⇒ r = 70
∴ Radius = 70 cm
Que-6: Find the radii of the circles if circumference is : (π = 3.14)
(i) 100 m
(ii) 6.4 dm
Sol: (i) Circumference = 100 m
Let radius of the circle = r
∴ 2πr = 100
⇒ 2 × 3.14 × r = 100
⇒ r = 100/(2×3.14) = (100×100)/(2×314)
= 10000/628 = 15.92 = 15.9 cm
∴ Radius = 15.9 cm
(ii) Circumference = 6.4 dm
Let radius of the circle = r
Then 2 πr = 6.4
⇒ 2 × 3.14 × r = 6.4
⇒ 6.28r = 6.4 ⇒ r = 6.4/6.28
⇒ r = 1.019 = 1.02 dm
∴ Radius = 1.02 cm
Que-7: The diameter of Venus planet is 12,278 km. Find its circumference.
Sol: Diameter of Venus planet = 12,278 km
Circumference = πd = (22/7) × 12278
= 22 × 1754 = 38588 km
Que-8: (i) Find the perimeter of semi-circular plate of radius 3.85 cm.
(ii) The circumference of a circle exceeds the diameter by 16.8 cm. Find the radius of the circle. (Take π = 22/7)
Sol: (i) Radius of the semicircle = 3.85 cm
Perimeter = πr + 2r
= (22/7) × 3.85 + 2 × 3.85
= 22 × 0.55 + 7.70
= 12.10 + 7.70 = 19.80 cm
(ii) Let r be the radius of the circle
∴ 2 πr – 2r = 16.8
⇒ 2r (π – 1) = 16.8
⇒ 2r ((22/7)−1) = 16.8 ⇒ 2r (15/7) = 16.8
⇒ r = (16.8×7)/(2×15) = (168×7)/(10×30) = (56×7)/100
= 392/100 = 3.92
∴Radius of the circle = 3.92 cm
Que-9: A wire is in form of a circle of radius 42 cm. It is bent into a square. Determine the side of square.
Sol: Radius of the circular wire = 42 cm
∴ Circumference = 2 πr = 2 × (22/7) × 42 cm = 264 cm
On bending it into a square,
The perimeter of square = 264 cm
∴ Side of the square = Perimeter / 4
= 264/4 = 66 cm
Que-10: In the figure, the radius is 3.5 cm. Find the perimeter of the quarter of the circle correct to one decimal place.
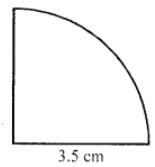
Sol: Radius of the quarter
Circle =3.5 cm
Perimeter = 2 πr × (1/4) + 2r
= (1/2) πr + 2r = (1/2) × (22/7) × 3.5 + 2 × 3.5
= 5.5 + 7.0 = 12.5 cm
Que-11: (i) The inner circumference of a circular track is 440 m. The track is 14 m wide. Find the diameter of the outer circle of the track. (Take π = 22/7)
(ii) The inner edge of a circular running-track is 440 m long. If the track is 10 m wide, find the length of the outer edge of the track.
Sol: (i) The inner circumference of the circular track = 440 m

Radius (r) = circumference 2π
= (440×7)/(2×22) = 70 m
Width of track = 14 m
∴ Radius of the outer circle (R)
= 70 + 14 = 84 m
and diameter = 2R = 2 × 84 = 168 m
(ii) The inner edge of the circular track = 440 m
∴ Inner radius (r) = circumference / 2π
= (440×7)/(22×2) = 70 m
Width of track = 10 m
∴ Outer radius (R) = 70 + 10 = 80 m
∴ Length of outer edge (circumference)
= 2πR = 2 × (22/7) × 80 = 3520/7 m = 502.86 m
Que-12: A garden roller has a circumference of 3 metres. How many revolutions does it make in moving a distance of 21 metres?
Sol: Circumference of roller = 3 m
Distance travelled = 21 m
∴ Number of revolutions will be
= Distance / circumference = 21/3 = 7
Que-13: A bicycle wheel, diameter 70 cm, is making 25 revolutions in 10 sec. At what speed in km/hr is the bicycle travelling?
Sol: Diameter of the cycle wheel (d) = 70 cm
∴ Circumference = πd = (22/7) × 70 = 220 cm
Distance travelled in 25 revolutions
=220 × 25 = 5500 cm = 55 m
∴ Distance of 55 m travelled in = 10 sec.
∴ The distance travelled in 1 hour
= (55/10) × 60 × 60 m = 19800 m = 19.8 Km
∴ Speed = 19.8 km/hour
Que-14: A small cart is being driven at 10 km per hour. If each wheel is 91 cm in diameter, find the number of revolutions made by each wheel per minute.
Sol: Diameter of wheel (d) = 91 cm
∴ Circumference = πd = (22/7) × 91 = 286 cm
Speed = 10 km/hr.
Distance travelled in 1 hour = 10 km
∴ Distance travelled in 1 minute = (10/60) Km
= (10×1000)/60 m = 500/3 m
∴ Number of revolutions in one minute
= (500/3) × (100/286) (circumference = 286cm)
= (500×50)/(3×143) = 25000/429 = 58*(118/429)
Que-15: How long will a boy take to go four times round a circular field whose radius is 35 m, walking at 5 km per hour ?
Sol: Radius of circular field (r) = 35 m
∴ Circumference = 2πr = 2 × (22/7) × 35 = 220 m
Distance travelled in 4 rounds = 220 × 4 m = 880 m
Speed of walking = 5km/hour
∴ Time taken to travelled 880 m = 880/5000 hr.
= (880×60)/5000 = 264/25 = 10.56 minute
= 10 minute 34 second (approx)
Que-16: A wheel of a cart is making 4 revolutions per second. If the diameter of the wheel is 84 cm, find its speed.
Sol: Diameter of the wheel of the cart (d) = 84 cm
∴ Circumference = πd = (22/7) × 84 = 264 cm
Distance covered in 1 sec = 4 revolutions
= 4 × 264 = 1056 cm
∴ Distance covered in 1 hour
= 1056 × 60 × 60 cm = (1056×60×60)/(100×1000) km
= 38016/1000 = 38.016 km
∴ Speed of the cart = 38.016 km/hr
Que-17: The figure shows a running track in which AF = CD = 100 m and FED and ABC are semicircles whose diameters FD and AC are equal. How much will an athlete run in taking one complete round of the track?
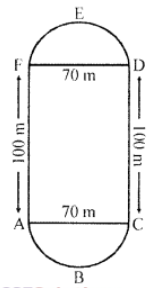
Sol: Diameter of semicircular part = 70 m
∴ Circumference of two semicircular part
= 2 × (1/2)πd = πd = (22/7) × 70 = 220 m
∴ Length of one complete round
= ABC + DEF + AF + CD
= 220 + 100 + 100
= 420 m.
Que-18: A circular field has a perimeter of 660 m. A plot in the shape of a square having its vertices on the circumference is marked in the field, calculate the area of the square plot.
Sol: Perimeter (circumference) of the circular field = 660 m
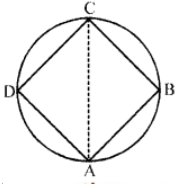
Radius (r) = circumference / 2π
= (660×7)/(22×2) = 105 m
Join AC
∴Length of diagonal of square ABCD
= diameter of the circle = 2r
= 2 × 105 = 210 m
Area of square plot = (diagonal)²/2
= (210)²/2 = (210×210)/2
= 22050 m².
–; End of Circle Circumference and Area Class 9 OP Malhotra Exe-17A ICSE Maths Solutions Ch-17 :–
Return to :– OP Malhotra S Chand Solutions for ICSE Class-9 Maths
Thanks
Please Share with Your Friends


