Circle Class 9 OP Malhotra Exe-13B ICSE Maths Solutions Ch-13

Circle Class 9 OP Malhotra Exe-13B ICSE Maths Solutions Ch-13. We Provide Step by Step Solutions / Answer of Questions of OP Malhotra Maths. Visit official Website CISCE for detail information about ICSE Board Class-9 Mathematics.

Board	ICSE
Publications	S Chand
Subject	Maths
Class	9th
Chapter-13	Circle
Writer	OP Malhotra
Exe-13B	Solved Problems on Circle
Edition	2025-2026

Exercise- 13B

Circle Class 9 OP Malhotra Exe-13B ICSE Maths Solutions Ch-13

Que-1: Find :

Sol: (i) ∵ Angles at a point = 360°
∴ 4x – 2 + 6x + 6 + 7x – 18 = 360°
⇒ 17x – 14 = 360°
⇒ 17x = 360° + 14
⇒ 17x = 374°
⇒ x = 374°/17 = 22°
Now, m QR = 7x – 18 = 7 x 22 – 18°
= 154°- 18° = 136°

(ii) ∵ AD is the diameter of the circle with centre O
∴ m ∠AOD = 180°
∴ 10y = 180° ⇒ y = 180°/10= 18°
Now, m ∠BOC = 6y = 6 x 18 = 108°

(iii) In the figure, AC = BC
∴ ∠AOC = ∠BOC
∴ 8y – 8 = 6y
⇒ 8y – 6y = 8
⇒ 2y = 8
⇒ y = 4
∴ m ∠AOC = 8y – 8 = 8 x 4 – 8 = 32 – 8 = 24°
∴ m ∠AOC = 24°

(iv) In the given figure, ⊙ A = ⊙ B
⇒ Circles with centres A and B are equal
and CD = EF
45 – 6x = 9x ⇒ 45 = 9x + 6x
⇒ 15x = 45 ⇒ x = 45/15 = 3
Now, m ∠EBF = 9x = 9 x 3 = 27°
OR
If m ∠CAD = 45 + 6x, then
45 + 6x = 9x ⇒ 45 = 9x – 6x
⇒ 3x = 45 ⇒ x = 45/3 = 15
m(∠EBF) = 9x = 9 x 15 = 135°

(v) In the given figure, a circle with centre O and QT and PS are diameters
m PR = PQ + m QR
= m ST + mQR
(∵ ∠POQ = ∠SOT vertically opposite angles)
= 55° + 100° = 155°
and m PRT = m ∠PQ + m 2∠QRT
= 55° + 180° = 235°

(vi) In the figure, chord AB = chord CD
∴ 4y + y = y + 68°
(Angles at the centre by two equal chords are equal)
5y = y + 68° ⇒ 5y – y = 68°
⇒ 4y = 68°
⇒ y = 68°/4 = 17°
m AB = 4y + y = 5y
= 5 x 17° = 85°

Que-2: ∆PQR is inscribed in a circle. ∠P = ∠Q. Prove that PR = QR.

Sol: ∆ABC is inscribed in a circle and ∠P = ∠Q
∴ QR = PR

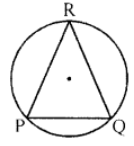
∵ Equal chords subtend equal angles at the centre
∴ mPR = mQR

Que-3: Given AB = CD. Prove that AC = DB.

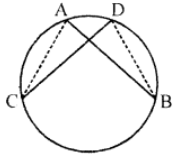
Sol: In the given figure,
AB = CD
AC and BD are joined
To prove : AC = DB
∵ AB = DC
∴ m AB = m DC
Subtracting m AD from both sides
∴ m AB – AD = m DC – m AD
⇒ m AC = m DB
⇒ AC = DB
Hence proved.

Que-4: Given AC = BD. Prove that AB = CD.

Sol: AB = DC
∵ AC = DB
∴ 12
Adding m AD to both sides
AC + DB = AD + DB
CD = AB
CD = AB ⇒ CD = AB
Hence AB = CD

Que-5: In figure, X, Y are the middle points of the arcs AB, AC. Prove that AP = AQ.

Sol: Given : in the circle,
AB and AC are two arcs.
X and Y are the midpoints of arc AB and arc AC.
XY is joined which meet AB in P and AC in Q
Construction : Join AX, AY, BX and BY

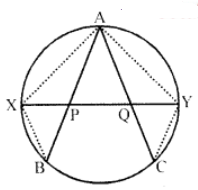
AB = AC
∴ arc AXB = arc AYC
But X and Y are the midpoints of AB and AC
∴ AX = XB and AY = YC
∴ ∠XAY = ∠XBA and ∠YAC = ∠YCA
∴ ∠XAB or ∠XAP = ∠YAQ
Now in ∆XAP and ∆YAQ
AY = AY (common)
∠XAP = ∠YAQ (proved)
∠AXP = ∠AYQ (proved)
∴ ∆XAP ≅ ∆YAQ (AAS axiom)
∴ AP = AQ (c.p.c.t.)
Hence proved.

Que-6: Circle O with chords AB = BC = CD = DE. Prove that AD = BE.

Sol: Given : In a circle with centre O, chord AB = BC = CD = DE
AD and BE are joined
Construction : Join AO, BO, CO, DO and EO

AB = BC = CD = DE(given)
∴ AB + BC + CD = AD
Similarly BC + CD + DE = BE
AB + BC + CD = BC + CD + DE
⇒ AD = BE
∴ Central ∠AOD = central ∠BOE Now in ∆AOD and ∆BOE,
OA = OB
OD = OE (radii of the same circle)
∠AOD = ∠BOE (proved)
∴ ∆AOD = ∆BOE (SAS axiom)
∴ AD = BE (c.p.c.t.)
Hence proved.

Que-7: In figure, APB and CQD are two congruent arcs. Prove that AC || BD.

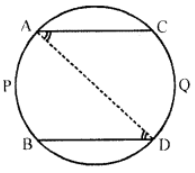
Sol: Given : In a circle, arc APB = arc COD
AC and BD are joined
To prove : AC = BD
Construction : Join AD
Proof: ∵ Arc APB = arc CQD (given)
∴ ∠ADB = ∠CAD
{Equal arcs subtends equal angles at the circumference}
But these are alternate angles
∴ AC || BD
Hence proved.

Que-8: In figure, ABC is equilateral, P and S are midpoints of arcs AB and AC. Prove that PQ = QR = RS.

Sol: In the figure, equilateral ∆ABC is inscribed in a circle
P and S are midpoints of arcs AB and AC respectively
Construction : Join AP, BP, AS and CS

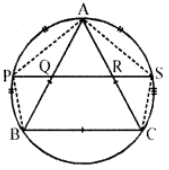
P is the midpoint of arc AB and S
is the midpoint of arc AC
∴ AP = PB and AS = SC
∠PAB = ∠PBA and ∠CAS = ∠SAC
But AB = AC (Side of equilateral triangle)
∴ ∠PAB = ∠PBA = ∠CAS = ∠SAC
Now in ∆APQ and ∆ASR,
AP = AS
∠PAQ = ∠SAR (∵ ∠PAB = ∠SAC)
and ∠APQ = ∠ASR (∵ AP = AS)
∴ ∆PAQ ≅ ∆ASR (AAS axiom)
∴ PQ = RS (c.p.c.t) … (i)
Now ∵ ∠PAQ = ∠SAR
Adding ∠QAR to both sides
∴ ∠PAQ + ∠QAR = ∠QAR + ∠SAR
⇒ ∠PAR = ∠SAQ
Now in ∆PAR and ∆SAQ,
AP = AS (proved)
∠PAR = ∠SAQ (proved)
∠APQ = ∠ASR (proved)
∴ ∆PAR ≅ ∆SAQ (AAS axiom)
∴ PR = QS … (ii)
Subtracting (i) and from (ii)
PR – PQ = QS – RS
QR = QR
∴ PQ = QR = RS
Hence proved.

Que-9: Each side of a regular hexagon, inscribed in a circle subtends an angle of 60° at the centre and is equal to the radius of the circle. Prove it.

Sol: Given : A regular hexagon ABCDEF inscribed in a circle with centre O
Join AO, BO, CO, DO, EO and FO

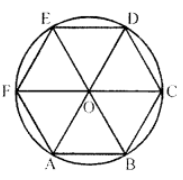
AB = BC = CD = DE = EF = FA
(Sides of regular hexagon)
∴ AB = BC = CD = DE = EF = FA
∴ Each arc will subtends angle at the centre
= 360°/6 = 60°
Hence proved.