Circles Class 10 OP Malhotra Exe-14A ICSE Maths Solutions

Circles Class 10 OP Malhotra Exe-14A ICSE Maths Solutions Ch-14 questions as latest prescribe guideline for upcoming exam. In this article you would learn Angle Properties of a Circle. Visit official Website CISCE for detail information about ICSE Board Class-10 Mathematics.

Circles Class 10 OP Malhotra Exe-14A ICSE Maths Solutions Ch-14

Board	ICSE
Publications	S Chand
Subject	Maths
Class	10th
Chapter-14	Circles
Writer	OP Malhotra
Exe-14A	Angle Properties of a Circle
Edition	2024-2025

Angle Properties of a Circle

The angle subtended by an arc at the center is double the angle subtended by it at any point on the remaining part of the circle

• Inscribed angles subtended by the same arc are equal.
• Central angles subtended by arcs of the same length are equal.
• The central angle of a circle is twice any inscribed angle subtended by the same arc.
• Angle inscribed in semicircle is 90°.
• An angle between a tangent and a chord through the point of contact is equal to the angle in the alternate segment.
• The opposite angles of a cyclic quadrilateral are supplementary
• The exterior angle of a cyclic quadrilateral is equal to the interior opposite angle.
• A radius or diameter that is perpendicular to a chord divides the chord into two equal parts and vice versa.
• A tangent to a circle is perpendicular to the radius drawn to the point of tangency.
• When two segments are drawn tangent to a circle from the same point outside the circle, the segments are equal in length.

Exercise- 14A Angle Properties of a Circle

Circles Class 10 OP Malhotra Exe-14A ICSE Maths Solutions Ch-14 questions

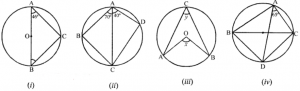
Que-1: Fill up the blanks :

(i) O is the centre of the circle, ∠BAC = 46°, ∠ABC ………………………
(ii) If ∠BAC = 70° and ∠DAC = 40°, then ∠BCD = …………..
(iii) O is the centre of the circle. If ∠x = 120°, then ∠y = …………….
(iv) BC is a diameter of the circle and ∠CAD = 65°, then ∠BCD = …………..

Sol: (i) AB is diameter of the circle
∴ ∠ACB = 90° (Angle in a semicircle)
∴ ∠BAC + ∠ABC = 90°
⇒ 46° + ∠ABC = 90°
⇒ ∠ABC = 90°- 46° = 44°

(ii) AC is diameter of the circle
∴∠ADC = ∠ABC = 90° (Angle in a semicircle)
∴∠BAC + ∠BCA = 90°
⇒ 70° +∠BCA = 90°
⇒ ∠BCA = 90° – 70° = 20°
and ∠DAC + ∠DCA = 90°
⇒ 40° + ∠DCA = 90°
⇒ ∠DAC = 90° – 40° = 50°
∴ ∠BCD = ∠BCA + ∠ACD = 20° + 50° = 70°

(iii) Arc AB subtends ∠AOB at the centre and ∠ACB at the remaining part of the circle
∴ ∠AOB = 2 ∠ACB
⇒ ∠x = 2 ∠y ⇒ 2 ∠y = 120°
⇒ ∠y = 120°/2 = 60°
∴ ∠y = 60°

(iv) BC is the diameter of the circle
∴ ∠BAC = 90° (Angle in a semicircle)
⇒ ∠BAD + ∠DAC = 90°
⇒ ∠BAD + 65° = 90°
⇒ ∠BAD = 90°- 65° = 25°
But ∠BCD = ∠BAD (Angles in the same segment)

Que-2: In the figure, O is the centre of the circle. ∠OAB and ∠OCB are 30° and 40° respectively. Find ∠AOC. Show your steps of working.

Sol: In the figure, O is the centre of the circle ∠OAB = 30° and ∠OCB = 40°
Join OB
In △OAB, OA = OB (radii of the semicircle)
∴ ∠OBA = ∠OAB = 30°
Similarly in △OBC, OB = OC
∴ ∠OBC = ∠OCB = 40°
∴ ∠ABC = ∠OBA + ∠OBC = 30° + 40° = 70°
Now arc AB subtends ∠AOC at the centre and ∠ABC at the remaining part of the circle
∴ ∠AOC = 2∠ABC = 2 × 70° = 140°
∴ ∠AOC = 140°

Que-3: In Fig., O is the centre of the circle. Given ∠AOB = 80°.Calculate the value of ∠OAB and ∠OAC.

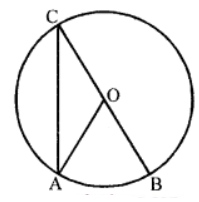
Sol: In the figure, O is the centre and BOC is the diameter of the circle ∠AOB = 80°
AC and AB are joined
Now arc AB subtends
∠AOB at the centre and ∠ACB at the remaining part of the circle
∴ ∠AOB = ∠ACB
⇒ 80° = 2∠ACB ⇒ ∠ACB = 80°/2 = 40°
But in △OAC, OA = OC (radii of the semicircle)
∴ ∠OAC = ∠OCA = ∠ACB = 40°
But ∠BAC = 90° (Angle in the semicircle)
⇒ ∠OAC + ∠OAB = 90°
⇒ 40° + ∠OAB = 90°
⇒ ∠OAB = 90°- 40° = 50°
Hence ∠OAB = 50° and ∠OAC = 40°

Que-4: In figure, O is the centre of the circle. If ∠AOB = 140° and ∠OAC = 50°. Find

(i) ∠ACB
(ii) ∠OBC
(iii) ∠OAB
(iv) ∠CBA

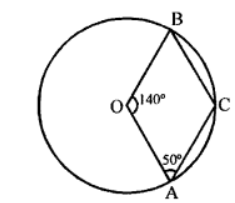
Sol: In the figure, O is the centre of the circle ∠AOB = 140°, ∠OAC = 50°
Join AB
∴ Reflex ∠AOB = 360° – 140° = 220°
Now major arc AB subtends
Ref. ∠AOB at the centre and ∠ACB at the remaining part of the circle
(i) ∴Ref. ∠AOB = 2∠ACB
⇒ 220° = 2∠ACB ⇒ ∠ACB = (1/2) × 220°
⇒ ∠ACB =110°

(ii) In quad. OACB,
∠BOA + ∠OAC + ∠ACB + ∠OBC = 360°
⇒ 140° + 50° + 110° + ∠OBC = 360°
⇒ 300° + ∠OBC = 360°
⇒ ∠OBC = 360° – 300° = 60°

(iii) ∠OAB + ∠OBA + ∠AOB = 180°
⇒ ∠OAB + ∠OBA + 140°= 180°
⇒ 2∠OAB = 180° – 140° = 40°
∴ ∠OAB = 40°/2 = 20°

(iv) In △ABC,
∠BAC + ∠CBA + ∠ACB = 180°
⇒ 30° + ∠CBA + 110° = 180°
(∵ ∠BAC = ∠OAC – ∠OAB = 50° – 20° = 30°)
⇒ 140° +∠CBA = 180°
⇒ ∠CBA = 180° – 140° = 40°

Que-5: In figure, if ∠ABC = 50° and ∠BDC = 40°, calculate

(i) ∠CDA
(ii) ∠BAC
(iii) ∠BCA

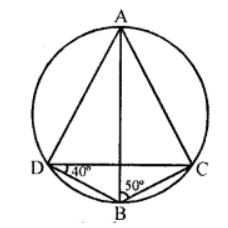
Sol: 

(i) In the figure, ∠ABC = 50°, ∠BDC = 40°
AB is the diameter of the circle
∵ ∠BDA = 90° (Angle in a semicircle)
∴ ∠CDA = ∠BDA – ∠BDC = 90°- 40° = 50°

(ii) ∠BCA = 90° (Angle in a semicircle)
∴ ∠BAC + ∠ABC = 90°
⇒ ∠BAC + 50° = 90° ⇒ ∠BAC = 90° – 50°
⇒ ∠BAC = 40°
Hence (i) ∠CDA = 50°, (ii) BAC = 40° and (iii) ∠BCA = 90°

Que-6: In figure, AC is a diameter of the given circle and ∠BCD = 75°. Calculate the size of : (i) ∠ABC, (ii) ∠EAF

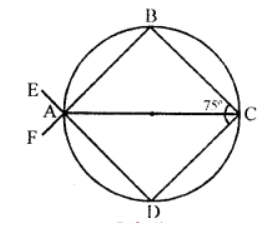
Sol: In the figure, AC is the diameter of the circle and ∠BCD = 75°
(i) ∠ABC = 90° (Angle in a semicircle)
(ii) ∠BCD + ∠BAD = 180° (Opposite angles of a cyclic quad.)
⇒ 75° + ∠BAD = 180°
⇒ ∠BAD = 180° – 75° = 105°
But ∠EAF = ∠BAD = 105° (Vertically opposite angles)
∴ ∠EAF = 105°

Que-7: In fig., ABCD is a quadrilateral inscribed in a circle with centre O. CD is produced to E. If ∠ADE = 70° and ∠OBA = 45°, calculate ∠BAC and ∠OCA.

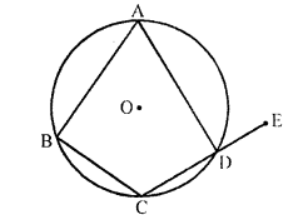
Sol: A quadrilateral ABCD which is inscribed ina circle with centre O. CD is produced to E ∠ADE = 70° and ∠OBA = 45°
Join OA, OB, OC, AC
ABCD is a cyclic quadrilateral
∴ Ext. ∠ADE = Interior opposite ∠ABC
∴ ∠ABC = 70° (∠ADE = 70°)
Arc AC subtends ∠AOC at the centre and ∠ABC on the remaining part of the circle
∴ ∠AOC = 2∠ABC = 2 × 70°= 140°
Now in △OAC, OA = OC (radii of the same circle)
∴ ∠OCA = ∠OAC
But ∠OCA + ∠OAC + ∠AOC = 180° (sum of angles of a △)
⇒ ∠OCA + ∠OCA + 140° = 180°
⇒ 2∠OCA = 180° – 140° = 40°
∴ ∠OCA = 40°/2 = 20°
and ∠OAC = 20°
Now ∠BAC = ∠BAO + ∠OAC
= 45° + 20° = 65° (∵ ∠BAO = ∠ABO = 45°)
Hence (i) ∠BAC = 65° and (ii) ∠OCA = 20°

Que-8: In figure, O is the centre of the circle. Calculate the values of x and y.

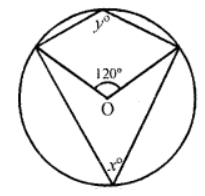
Sol: In the figure, ABCD is a cyclic quadrilateral in which O is the centre of the circle
∠AOC = 120°
But ∠AOC + ref. ∠AOC = 360°(Angles at a point)
Ref. ∠AOC = 360° – ∠AOC = 360° – 120° = 240°
Now arc ADC subtends ∠AOC at the centre and ∠ABC at the remaining part of a cyclic
∴ ∠AOC = 2∠ABC ⇒ 120° = 2x
⇒ x = 120°/2 = 60°
But ∠B + ∠D = 180°
(Sum of opposite angles of a cyclic quadrilateral)
⇒ x + y = 180°
⇒ 60° + y = 180°
⇒ y = 180°- 60°
⇒ y = 120°
Hence x = 60° and y – 120°

Que-9: In fig. AB || CD and O is the centre of the circle. If ∠ADC = 25°, find ∠AEB. Give reasons in support of your answer.

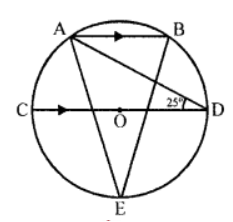
Sol: In the figure, AB || CD O is the centre of the circle and ∠ADC = 25°
Join OA and OB
∵ AB || CD
∴ ∠BAD = ∠ADC = 25° (Alternate angles)
In △OAD, OA = OD (radii of the same circle)
∴ ∠OAD = ∠ADO or ∠ADC = 25°
∴ ∠OAB = ∠OAD + ∠BAD = 25° + 25° = 50°
But in △OAB,
OA = OB (radii of the same circle)
∴ ∠OAB = ∠OBA = 50°
But ∠OAB + ∠OBA + ∠AOB = 180° (Angles of a triangle)
⇒ 50° + 50° + ∠AOB = 180°
⇒ ∠AOB+ 100°= 180°
⇒ ∠AOB = 180° – 100° = 80°
Now arc AB, subtends ∠AOB at the centre and ∠AEB at the remaining part of the circle
∴ ∠AOB = 2∠AEB
⇒ ∠AEB = 1/2 (AOB = (1/2)×80°=40°)
Hence ∠AEB = 40°

Que-10: In the fig, AB || CD. If ∠BCD = 100° and ∠BAC = 40°, calculate

(i) ∠CAD
(ii) ∠CBD
(ii) ∠BCA

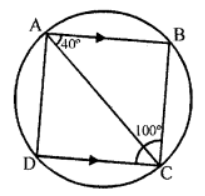
Sol: In the figure ABCD is a cyclic quadrilateral
in which AB || DC
∠BCD = 100° and ∠BAC = 40°
∴ AB || DC and AC is its transversal
∴ ∠BAC = ∠ACD = 40° (Alternate angles)
But ∠BCD = 100°
∴ ∠BCA = ∠BCD – ∠ACD =100° – 40° = 60°
∵ ABCD is a cyclic quadrilateral
∴ ∠BAD + ∠BCD = 180° (Sum of opp. angles)
⇒ ∠BAD + 100°= 180°
⇒ ∠BAD = 180° – 100° = 80°
⇒ ∠BAC + ∠CAD = 80°
⇒ 40° + ∠CAD = 80°
⇒ ∠CAD = 80° – 40° = 40°
But ∠CBD = ∠CAD (Angles in the same segment)
= 40°
Hence (i) ∠CAD = 40°, (ii) ∠CBD = 40°, (iii) ∠BCA = 60°

Que-11: In figure, ABCD is a parallelogram. A circle passes through A and D and cuts AB at E and DC at F. Given that ∠BEF = 80°, find ∠ABC.

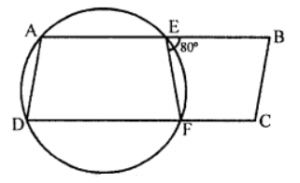
Sol: ABCD is a parallelogram
and a circle pass through A and D, intersects
AB at E and DC at F
EF is joined.
∠BEF = 80°
∵ ADFE is a cyclic quadrilateral
∴ Ext. ∠BEF = Int. opp. ∠ADF
∴ ∠ADF = 80° or ∠ADC = 80°
But in||gm ABCD
∠ADC = ∠ABC (opp. angles of a ||gm)
∴ ∠ABC = 80°

Que-12: In figure, if ∠BCD = 125° and AD is the diameter of the circle, calculate

(i) ∠DAB
(ii) ∠ADB

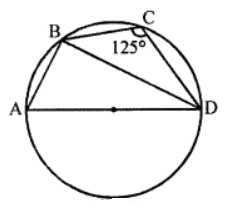
Sol: In the figure, AD is the diameter of the circle and ABCD is a cyclic quadrilateral ∠BCD = 125°
Join BD
(i) ∵ ABCD is a cyclic quadrilateral
∴ ∠BAD + ∠BCD = 180° (Sum of opposite angles)
⇒ ∠BAD + 125° = 180°
⇒ ∠BAD = 180° – 125° = 55°

(ii) Now in △ABD,
∠ABD = 90° (Angle in a semicircle)
∴ ∠BAD + ∠ADB = 90°
⇒ 55° + ∠ADB = 90°
⇒ ∠ADB = 90°- 55° = 35°
∴ ∠ADB = 35°
Hence (i) ∠BAD or ∠DAB = 55° and
(ii) ∠ADB = 35°

Que-13: In the figure, given a cyclic trapezium ABCD in which AD is parallel to BC and ∠B = 70°, find

(i) ∠BAD
(ii) ∠BCD

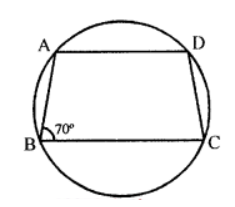
Sol:  In the figure, ABCD is a cyclic trapezium in which AD || BC and ZB = 70°
(i) ∵ AD || BC
∴ ∠ABC + ∠BAD = 180° (Sum of co-interior angles)
70° + ∠BAD = 180° => ∠BAD =180°- 70°
∴ ∠BAD = 110°

(ii) In cyclic trapezium,
∠BAD + ∠BCD = 180° (Sum of opposite angles)
110° + ∠BCD = 180°
⇒ ∠BCD = 180° – 110° = 70°
Hence ∠BAD =110°, ∠BCD = 70°

Que-14: In the figure AB is a diameter of the circle APBR, as shown in the figure. APQ and RBQ are straight lines; ∠A = 35°, ∠Q = 25°. Find :

(i) ∠PRB
(ii) ∠PBR
(iii) ∠BPR

Sol: In the figure, AB is the diameter of the circle APQ and RBQ are straight lines ∠A = 35° and ∠Q = 25°
(i) ∠PRB and ∠PAB are in the same segment
∴ ∠PRB = ∠PAB = 35°

(ii) In △PBQ,
Ext. ∠PBR = ∠BPQ + ∠Q
= 90° + 25° = 115°

(iii) In △BRP,
∠BRP + ∠PBR + ∠BPR = 180° (Sum of angles of a triangle)
⇒ 35° +115° + ∠BPR = 180°
⇒ 150° + ∠BPR = 180°
⇒ ∠BPR = 180°- 150° = 30°

Que-15: In the figure, it is given that O is the centre of the circle and ∠AOC = 130°. Find ∠ABC.

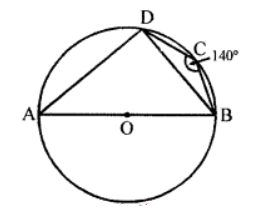
Sol: In the figure, O is the centre of the circle and ∠AOC = 130°
∴ Reflex ∠AOC = 360° – 130° = 230°
Now major arc AC subtends reflex ∠AOC at the centre and ∠ABC at the remaining part of the circle
∴ Reflex ∠AOC = 2∠ABC
⇒ 230° = 2∠ABC ⇒ ∠ABC = 230°/2 = 115°

Que-16: In the figure, AB is a diameter of the circle. If ∠BCD = 140°, find ∠DBA.

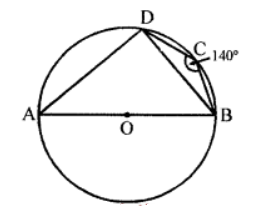
Sol: In the figure, AOB is the diameter of the circle
∠BCD = 140°
∵ ABCD is a cyclic quadrilateral
∴ ∠BCD + ∠BAD = 180° (Sum of opposite angles)
⇒ 140° + ∠BAD = 180°
⇒ ∠BAD = 180° – 140°
∠BAD = 40°
Now in △ADB,
∠ADB = 90° (Angles in a semicircle)
∴ ∠BAD + ∠DBA = 90°
⇒ 40° + ∠DBA = 90°
⇒ ∠DBA = 90°- 40° = 50°

Que-17: In the figure, O is the centre of the circle, ABD is a st. line and ∠CBD = 65°. Find

(i) ∠AEC,
(ii) ∠AOC (marked x°)

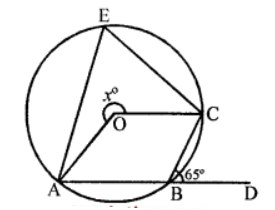
Sol: In the figure, ABCE is a cyclic quadrilateral in which AB is produced to D ∠CBD = 65°
∵ ABCE is a cyclic quadrilateral
∴ Ext. ∠CBD = Interior opposite ∠AEC
⇒ ∠AEC = ∠CBD = 65°
∵ Arc ABC subtends ∠AOC at the centre and ∠AEC at the remaining part of the circle
∴ ∠AOC = 2∠AEC = 2 × 65° = 130°
But ∠AOC + reflex ∠AOC = 360° (Angles at a point)
⇒ 130° + x° = 360° ⇒ x° = 360° – 130° = 230°

Que-18: In figure, the diagonals of a cyclic quadrilateral ABCD intersect in P and the area of the triangle APB is 24 cm². If AB = 8 cm, and CD = 5 cm, calculate the area of the ACPD.

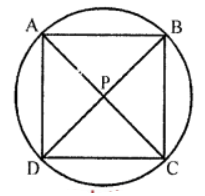
Sol: In the figure,
Two diagonals of a cyclic quadrilateral ABCD intersect each other at P inside the circle. AB = 8 cm, CD = 5 cm and area (AAPB) = 24 cm2
∵ Diagonals AC and BD intersect each other at P
∴ AP.PC = BP.PD
⇒ AP/BP = DP/CP
⇒ AP/DP = BP/CP (By alternend0)
and ∠APB = ∠CPD (Vertically opposite angles)
∴△APB ~ △CPD (SAS axiom)
{area △APB}/{area △CPD} = AB²/CD²
24/{area △CPD} = 8²/5²
24//{area △CPD} = 64/25
{area △CPD} = (24×25)/64
{area △CPD} = 75/8 = 9*(3/8) cm²

Que-19: In figure, O is the centre of the circle. If ∠BAD = 30°, find the values of p, q and r.

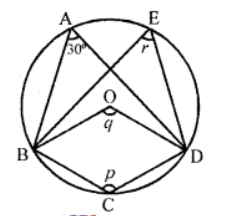
Sol: In the figure,
(i) O is the centre of the circle and ∠BAD = 30°
∵ ABCD is a cyclic quadrilateral
∴ ∠BAD + ∠BCD = 180° (Sum of opposite angles)
⇒ 30 °+ p = 180°
⇒ p = 180°- 30° = 150°
Arc BCD subtends ∠BOD at the centre and ∠BAD at the remaining part of the circle
∴ ∠BOD = 2∠BAD
q = 2 × 30° = 60°
∴ ∠BAD and ∠BED are in the same segment
∴ ∠BED = ∠BAD
⇒ r = 30°
Hence p = 150°, q = 60° and r = 30°

Que-20: In figure, if ∠BAD = 65°, ∠ABD = 70°, ∠BDC = 45°, calculate

(i) ∠BCD
(ii) ∠ADB and show that AC is a diameter

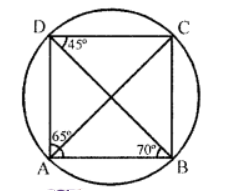
Sol:  (i) In the figure, ABCD is a cyclic quadrilateral in which its diagonals AC and BD intersect each other at P
∠BAD = 65°, ∠ABD = 70°, ∠BDC = 45°
∵ ABCD is a cyclic quadrilateral ∠BAD + ∠BCD= 180° (Sum of opposite angles)
⇒ 65° + ∠BCD = 180°
⇒ ∠BCD = 180° – 65° = 115°

(ii) In △ABD,
∠BAD + ∠ABD + ∠ADB = 180° (Sum of angles of a triangle)
⇒ 65° + 70° + ∠ADB = 180°
⇒ 135° + ∠ADB = 180°
⇒ ∠ADB = 180° – 135° = 45°
∵ ∠ADC = ∠ADB + ∠BDC = 45° + 45° = 90°
∴ ADC is a semicircle
Hence AC is the diameter of the circle

Que-21: In figure, AB is a diameter of the circle whose centre is O. Given that ∠ECD = ∠EDC = 32°. Calculate :

(i) ∠CEF
(ii) ∠COF

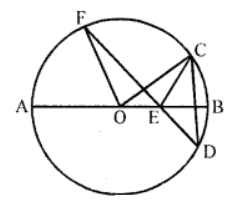
Sol: In the figure, AOB is the diameter of the circle with centre O
∠ECD = ∠EDC = 32°
(i) In △CDE,
Ext. ∠CEF = ∠ECD + ∠EDC = 32° + 32° = 64°
(ii) Arc CF subtends ∠COF at the centre and ∠CDE or ∠CEF at the remaining part of the circle
∴ ∠COF = 2∠CDF = 2 × 32° = 64°

Que-22: In figure, ABCD is a cyclic quadrilateral in which ∠DAC = 27°, ∠DBA = 50°, ∠ADB = 33°. Calculate :

(i) ∠DBC,
(ii) ∠DCB,
(iii) ∠CAB

Sol: In the figure, ABCD is a cyclic quadrilateral AC and BD are joined
∠DAC = 27°, ∠DBA = 50°, ∠ADB = 33°
∠ADB = ∠ACB (Angles in the same segment)
∴ ∠ACB = 33°
Similarly ∠ABD = ∠ACD (Angles in the same segment)
∴ ∠ACB = 50°
∴ ∠DCB = ∠ACB + ∠ACD = 33° + 50°= 83°
In cyclic quad. ABCD
∠DCB + ∠BAD = 180°
⇒ 83° + ∠BAD = 180°
⇒ ∠BAD = 180°- 83° = 97°
⇒ ∠BAC + ∠DAC = 97°
⇒ ∠BAC + 27° = 97°
⇒ ∠BAC = 97° – 27° = 70°
or ∠CAB = 70°
∠DBC = ∠DAC (Angles in the same segment)
= 27°
Hence (i) ∠DBC = 27°, (ii) ∠DCB = 83°, ∠CAB = 70°

Que-23: The diagram (see figure) shows a pentagon ABCDF inscribed in a circle, centre O. Given AB = BC = CD and ∠ABC = 132°. Calculate the value of

(i) ∠AEB
(ii) ∠AED
(iii) ∠COD

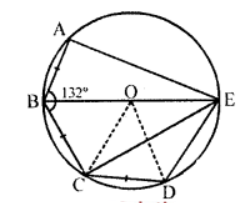
Sol: In the figure, ABCD E is a pentagon inscribed
in the circle with centre O
AB = BC = CD and ∠ABC = 132°
Join BE and CE
(i) In cyclic quad. AECB,
∠AEC + ∠ABC = 180° (Sum of opposite angles)
⇒ ∠AEC + 132°= 180°
⇒ AEC = 180° – 132° = 48°
∵ AB = BC
∠AEB = ∠BEC
= 48°/2 = 24°

(ii) ∵ AB = BC = CD
∴ ∠AEB = ∠BEC = ∠CED = 24°
∴ ∠AED = ∠AEB + ∠AEC + ∠CED
= 24° + 24° + 24° = 72°

(iii) Arc CD subtends ∠COD at the centre and ∠CED at the remaining part of the circle
∴ ∠COD = 2∠CED = 2 × 24° = 48°

Que-24: In the given circle with diameter AB, find the value of x.

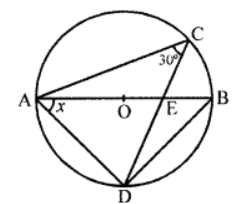
Sol: In the given figure, AB is the diameter of the circle with centre O
∠ACD = 30° and ∠DAB = x
Join BC
∠ACB = 90° (Angle in a semicircle)
∴ ∠BCD = ∠ACB – ∠ACD = 90° – 30° = 60°
But ∠BAD = ∠BCD (Angles in the same segment)
∴ x = 60°

Que-25: In figure, PQ is the diameter of the circle whose centre is O. Given ∠ROS = 42°, Calculate ∠RTS.

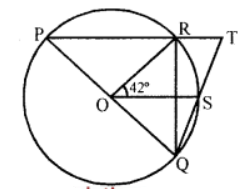
Sol: In the figure, PQ is the diameter of the circle whose centre is O, ∠ROS = 42°
∠PRQ = 90° (Angle in a semicircle)
But ∠QRT + ∠PRQ = 180° (Linear pair)
⇒ ∠QRT + 90°= 180°
⇒ ∠QRT = 180°- 90° = 90°
Arc RS subtends ∠ROS at the centre and ∠RQT at the remaining part of the circle
∴ ∠ROS = 2∠RQT
⇒ ∠RQT = (1/2) ∠ROS = (1/2) × 42° = 21°
Now in △RQT
∠QRT + ∠RQT +∠RTS = 180° (Sum of angle of a triangle)
⇒ 90°+ 21° + ∠RTS = 180°
⇒ 111° + ∠RTS = 180°
⇒ ∠RTS = 180°- 111° = 69°

Que-26: In figure, PR is the diameter of the circle, PQ = 7 cm, QR = 6 cm and RS = 2 cm. Calculate the perimeter of the cyclic quadrilateral PQRS.

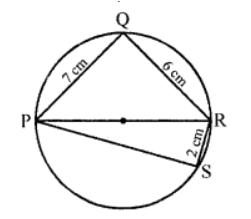
Sol: In the figure, PR is diameter of the circle PQRS is the cyclic quad, in which PQ = 7 cm, QR = 6 cm, RS = 2 cm
In △PQR, ∠Q = 90° (Angle in a semicircle)
∴ PR² = PQ² + QR² (Pythagoras Theorem)
= (7)² + (6)² = 49 + 36 = 85
Similarly, in △PSR, ∠S = 90°
PR² = PS² + RS²
85 = PS² + (2)² ⇒ PS² = 85 – 4 = 81 = (9)²
∴ PS = 9 cm
Now perimeter of PQRS
= PQ + QR + RS + PS
= 7 + 6 + 2 + 9 = 24 cm

Que-27: In the fig., AB = AC = CD, ∠ADC = 38°. Calculate : (i) ∠ABC, (ii) ∠BEC.

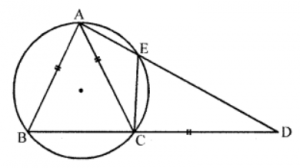
Sol:  In the given figure,
ABCE is a cyclic quadrilateral whose sides AE and BC are produced to meet at D and AB = AC = CD and ∠ADC = 38°
Join BE
In △ACD, AC = CD (given)
∴ ∠CAD = ∠ADC = 38°
In △ABC,
∵ AB = AC (given)
∴ ∠ABC = ∠ACB
But in △ACD,
Ext. ∠ACB = ∠CAD + ∠ADC = 38° + 38° = 76°
But ∠ABC = ∠ACB = 76°

(ii) In △ABC,
∠BAC =180°- (∠ABC + ∠ACB)
= 180° – (76° + 76°) = 180° – 152° = 28°
But ∠BAC = ∠BEC (Angles in the same segment)
∴ ∠BEC = 28°

–: End of Circles Class 10 OP Malhotra Exe-14A ICSE Maths Solutions Ch-14 :–

Return to :-  OP Malhotra S Chand Solutions for ICSE Class-10 Maths

Thanks

Please Share with Your Friends