Circles Class 10 OP Malhotra Exe-14C ICSE Maths Solutions

Circles Class 10 OP Malhotra Exe-14C ICSE Maths Solutions Ch-14 questions as latest prescribe guideline for upcoming exam. In this article you would learn to solve problems on Tangent Properties of a Circle. Visit official Website CISCE for detail information about ICSE Board Class-10 Mathematics.

Circles Class 10 OP Malhotra Exe-14C ICSE Maths Solutions Ch-14 Questions

Board	ICSE
Publications	S Chand
Subject	Maths
Class	10th
Chapter-14	Circles
Writer	OP Malhotra
Exe-14C	Tangent Properties of a Circle
Edition	2024-2025

Tangent Properties of a Circle

• The tangent always touches the circle at a single point.
• It is perpendicular to the radius of the circle at the point of tangency
• It never intersects the circle at two points.
• The length of tangents from an external point to a circle are equal.

Que-1: (a) In figure, APB is tangent to circle with centre O. If ∠QPB = 50°, find ∠POQ.

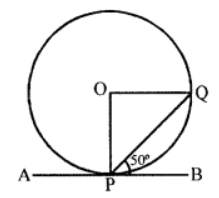
Sol:  (a) In the figure, APB is tangent to the circle
with centre O
∠QPB = 50°
∵ OP is the radius and APB is tangent
∴ OP ⊥ APB
∴ ∠OPB = 90° ⇒ ∠OPQ + ∠QPB = 90°
⇒ ∠OPQ + 50° = 90°
⇒ ∠OPQ = 90° – 50°
⇒ OPQ = 40°
But in △OPQ, OP = OQ (radii of the circle)
∴ ∠OPQ = ∠OQP = 40°
∠POQ + ∠OPQ + ∠OQP = 180°
⇒ ∠POQ + 40° + 40° = 180°
⇒ ∠POQ + 80°= 180°
∠POQ = 180° – 80 = 100°

(b) In figure, AB and AC are tangents. If AB = 4 cm, find AC.

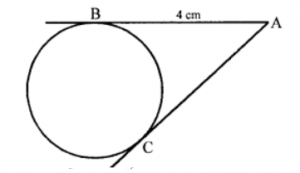
(b) In circle, two tangent AB and AC are drawn, a point A outside the circle
∴ AC = AB = 4 cm

(c) In the figure, PQ and PR are tangents to circle, centre O. If ∠QPR = 80°, find ∠QOR.

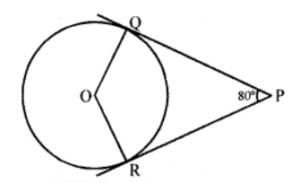
(c) In the figure, a circle with centre O from a point P outside the circle two tangents PQ and PR are drawn and ∠QPR = 80°
∴ ∠QPR and ∠QOR are supplementary ∠QPR + ∠QOR = 180°
⇒ 80° + ∠QOR = 180°
⇒ ∠QOR = 180° – 80° = 100°
∠QOR = 100°

Que-2: In figure, O is the centre of the circle. Find ∠POS.

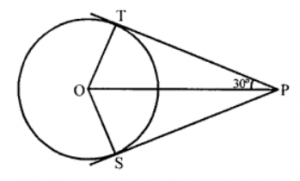
Sol: In the figure, a circle with centre O
From a point P outside of it, tangents PT and
PS are drawn to the circle, and ∠TPO = 30°
In △PTO, OT ⊥ PT
∴ ∠OTP = 90°
∴ ∠TOP + ∠TPO = 90°
⇒ ∠TOP + 30° = 90°
⇒ ∠TOP = 90°- 30° = 60°
∴ OP is the bisector of ∠TOS
∴ ∠TOP = ∠POS = 60°

Que-3: In figure, PQ is tangent to the circle at A, DB is a diameter, ∠ADB = 30° and ∠CBD = 60°, Calculate

(i) ∠QAB
(ii) ∠PAD
(iii) ∠CDB

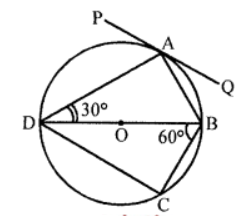
Sol:   In the figure, BD is the diameter of the circle PQ is tangent to the circle at A
∠ADB = 30°, ∠DBC = 60°

(i) ∵ QAP is tangent and AB is chord of the circle
∴ ∠QAB = ∠ADB = 30°

(ii) ∠PAD + ∠DAB + ∠QAB = 180° (Angles of a line)
⇒ ∠PAD + 90° + 30° = 180°
(∵ ∠DAB = 90° angle in semicircle)
⇒ ∠PAD + 120° = 180°
⇒ ∠PAD = 180° – 120° = 60°

(iii) In ABCD,
∠CDB + ∠CBD + ∠BCD = 180° (Sum of angles of a triangle)
⇒ ∠CDB + 60° + 90°= 180°
⇒ ∠CDB + 150° = 180°
⇒ ∠CDB = 180°- 150° = 30°

Que-4: In figure, PR and PQ are the tangents, each of them being equal to 9 cm, ∠QPR = 60°. Find the length of the chord QR which joins their points of contact.

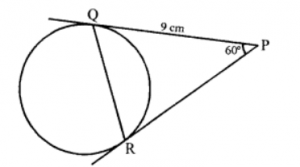
Sol: In the figure, PQ and PR the tangents drawn
from P outside the circle such that
PQ = PR = 9 cm and ∠QPR = 60°
QR is joined
In △PQR, ∠QPR = 60°
∵ PQ = PR
∴ ∠PQR = ∠PRQ = 60°
∴ △PQR is an equilateral triangle
PQ = PR = QR = 9 cm

Que-5: Find the length of the tangent drawn to a circle of radius 3 cm, from a point distant 5 cm from the centre.

Sol: In a circle of radius 3 cm, point P is 5 cm away from the centre O of the circle
PQ and PR are the tangents drawn from P to the circle
∵ OQ is radius and PQ is tangent
∴ OQ ⊥ QP or ∠OQP = 90°
Now in right angled △OPQ,
OP² = OQ² + PQ² (Pythagoras Theorem)
⇒ (5)² = (3)² + PQ²
⇒ 25 = 9 + PQ²
⇒ PQ² = 25 – 9 = 16 = (4)²
∴ PQ = 4 cm
But PQ = PR
∴ PQ = PR = 4 cm

Que-6: A circle touches the side BC of △ABC at P and touches AB and AC produced at Q and R respectively. If AQ = 5 cm, find the perimeter of △ABC.

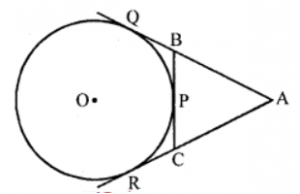
Sol: From A, AQ and AR are the tangents drawn to the circle
∴ AQ = AR = 5cm ….(i)
Similarly from B, tangent BQ and BP are drawn
∴ BQ = BP ….(ii)
and from C,
CR = CR ….(iii)
Now perimeter of △ABC,
= AB + AC + BC = AB + AC + BP + CP = AB + AC + BQ + CR [From (ii) and (iii)]
= AB + BQ + AC + CR
= AQ + AR = 5 cm + 5 cm [From (i)] = 10 cm

Que-7: There are two concentric circles of radii 3 cm and 5 cm respectively. Find the length of the chord of the outer circle which touches the inner circle

Sol: Two circles which are concentric and their centre is O, are of radii 5 cm and 3 cm
i. e. OA = 5 cm and OP = 3 cm
AB is chord of the larger circle which touches the smaller circle at P
∴ OP ⊥ AB ⇒ AP = PB
In right △OAP,
OA² = OP² + AP² (Pythagoras Theorem)
⇒ (5)² = (3)² + AP²
⇒ 25 = 9 + AP²
⇒ AP² = 25 – 9 = 16 = (4)²
∴ AP = 4 cm
Hence AB = 2AP = 2 × 4 = 8 cm

Que-8: Three circles with centres A, B, C touch each other externally; AB = 4 cm, BC = 6 cm, CA = 7 cm; find their radii.

Sol: ABC is a triangle and with centre A, B and C, three circles are drawn touching each other externally a t P, Q and R respectively AB = 4 cm, BC = 7 cm and AC = 6 cm

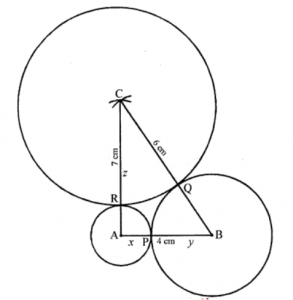
Let radii of circles with centre A, B and C respectively be x, y and z
∴ AB = x + y, BC = y + z, CA = z + x
⇒ x + y = 4 cm, y + z = 6 cm, z + x = 7 cm
∴ AB + BC + CA = x +y +y + z + z + x
⇒ 4 + 6 + 7 = 2(x + y + z)
⇒ x + y + z = 17/2 = 8.5 cm
Subtracting from x + y + z, we get
x = 8.5 – 4 = 4.5 cm
y = 8.5 – 6 = 2.5 cm
z = 8.5 – 7 = 1.5 cm
Hence their radii are 2.5 cm, 1.5 cm and 4.5 cm

Que-9: Equal circles, centres O and O’ touch each other at X. OO’ is produced to meet the circle O’ at A. AC is tangent to the circle whose centre is O. O’ is perpendicular to AC. Find the value of

(i) AO’/AO     (ii) {Area of ΔADO’}/{Area of ΔACO’}

Sol: Two equal circles with centres O and O’ touch each other externally at X. 00′ is produce to meet the circle O’ at A. Through A, a tangent AC is drawn to the circle with
centre O. O’D ⊥ AC
Let r be the radius of each circle
In △AO’D and △AOC,
∠D = ∠C (each 90°)
∠A = ∠A (common)
(i) △AO’D ∼ △AOC    (AA axiom)
AO’/AO = r/(AX+XO)
= r/(r+2r) = r/3r = 1/3
(ii)  {Area of ΔADO’}/{Area of ΔACO’}
= AO’²/AO² = (1/3)² = 1/9.

Que-10: In figure, P and Q are centres of two circles of radii 12 cm and 3 cm respectively. A and B are the points of contact of the common tangent XY. Find AB.

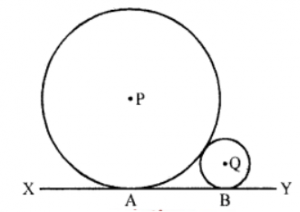
Sol: Two circles with centres P and Q touch externally at R
XY is their common tangent
A and B are their points of contact
Join PA, QB and PQ
From Q, draw QS || XY
∵ PA and QB are perpendicular to XY and
QS || AB
∴ QS = AB
PA = 12 cm, QB = 3 cm, PQ = 12 + 3 = 15 cm
∴ PS = PA – SA = 12 – 3 = 9 cm
Now in right △PSQ,
PQ² = PS² + QS² (Pythagoras Theorem)
⇒ (15)² = (9)² + QS²
⇒ 225 = 81 + QS²
⇒ QS² = 225 – 81 = 144 = (12)²
∴ QS = 12 cm
But AB = QS = 12 cm

–: End of Circles Class 10 OP Malhotra Exe-14C ICSE Maths Ch-14 :–

Return to :-  OP Malhotra S Chand Solutions for ICSE Class-10 Maths

Thanks

Please Share with Your Friends