Circles Class 10 OP Malhotra Exe-14D ICSE Maths Solutions Ch-14 questions as latest prescribe guideline for upcoming exam. In this article you would learn to solve complex problems on Tangent Properties of a Circle. Visit official Website CISCE for detail information about ICSE Board Class-10 Mathematics.
Circles Class 10 OP Malhotra Exe-14D ICSE Maths Solutions Ch-14
| Board | ICSE |
| Publications | S Chand |
| Subject | Maths |
| Class | 10th |
| Chapter-14 | Circles |
| Writer | OP Malhotra |
| Exe-14D | complex problems on Tangent Properties of a Circle |
| Edition | 2024-2025 |
Exercise- 14D (complex problems on Tangent Properties of a Circle)
Circles Class 10 OP Malhotra Exe-14D ICSE Maths Solutions Ch-14
Que-1: In figure, PA and PB are tangents from P to a circle with centre O. At M, a tangent is drawn cutting PA at K and PB at N. Prove that KN = AK + BN.
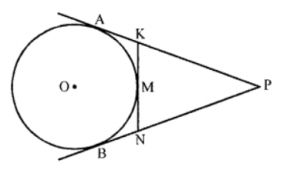
Sol: Given : In a circle with centre O, from a point P outside of it, PA and PB are the tangents to the circle.
At a point M, on the circle, another tangent is drawn which intersects AP at K and BP at N.
From K, KA and KM are tangents to
the circle.
∴ KA = KM ….(i)
Similarly from N, NM and NB tangents are drawn.
∴ NB = MN ….(ii)
Adding (i) and (ii)
KM + MN = KA + NB
KN=AK+BN
Hence proved.
Que-2: In figure, two concentric circles are given. Prove that every chord of the greater circle which is tangent to the smaller circle is bisected at its point of contact.
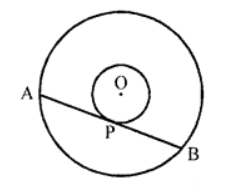
Sol: Given : Two concentric circles with centre O.
A chord AB is drawn to the greater circle which touches the smaller circle at P.
∵ OP is the radius and AB is the tangent
∴ OP ⊥ AB
In right △OAP and △OBP
Hyp. OA = OB (radii of the same circle)
Side OP = OP (common)
∴ △OAP ≅ △OBP (RHS axiom)
∴ AP = PB (c.p.c.t.)
Hence P bisects AB
Hence proved.
Que-3: Prove that the angle between two tangents drawn from an external point to a circle is supplementary to angle subtended by the line segments joining the points of contact at the centre.
Sol: A circle with centre O, from a point P outside of it, two tangents PT and PS are drawn TS is joined. Which subtends
∠TOS at the centre.
In right angle △OTP,
∠OTP = 90°
∴ ∠TOP + ∠TPO = 90° ….(i)
Similarly in right △OSP,
∠SOP + ∠SPO = 90° ….(ii)
Adding (i) and (ii)
∠TOP + ∠SOP + ∠TPO + ∠SPO = 90° + 90°
⇒ ∠TPS + ∠TOS = 180°
∠TPS and ∠TOS are supplementary
Hence proved.
Que-4: In figure, a circle touches the side be of a △ABC at X and AB and AC produced at Y and Z respectively. Prove that AY is half the perimeter of △ABC.
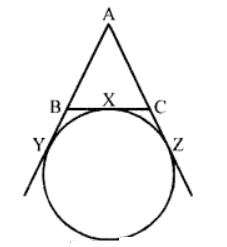
Sol: ∵ From A, AY and AZ are tangents to the circle
∴ AY = AZ
Similarly from B, BY and BX are tangents
∴ BY = BX
and from C, CX and CZ are tangents
∴ CZ = CX
Now AY = AB + BY = AB + BX
AZ = AC + CZ = AC + CX
∴ AY + AZ = AB + BX + CX + AC
⇒ AY + AY=AB + BC + CA (∵ AY = AZ)
⇒ 2AY = AB + BC + CA
⇒ AY = (1/2) (AB + BC + CA) Hence proved.
Que-5: In figure, the incircle of a △ABC touches the sides BC, CA and AB at D, E and F respectively. Show that AF + BD + CE = AE + CD + BF = (1/2) (perimeter of △ABC).
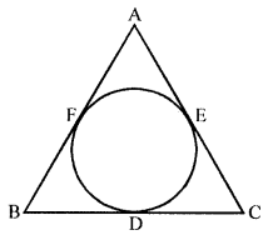
Sol: From A, AF and AE are the tangents to the circle
∴ AF = AE ….(i)
Similarly from B, BD and BF are the tangents
∴ BD = BF ….(ii)
and from C, CE and CD are the tangents
∴ CE = CD ….(iii)
Adding (i), (ii) and (iii) we get,
AF + BD + CE = AE + BF + CD
Adding to both sides
AF + BD + CE
2AF + 2BD + 2CE = AE + BF + CD + AF + BD + CE
2(AF + BD + CE) = AE + CE + BD + CD + AF + BF
⇒ 2(AF + BD + CE) = AC + BC + AB
⇒ AF + BD + CD = (1/2) (AB + BC + CA) Hence proved.
Que-6: Two circles touch each other externally. Show that the lengths of the tangents, drawn to the two circles from any point on the common tangents, are equal (See figure).
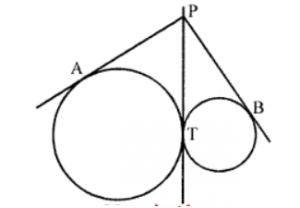
Sol: Two circles touch each other externally at T.
PT is their common tangent and from P, tangents PA and PB are drawn to the two circles
From P, PA and PT are the tangents to the bigger circle
∴ PA = PT ….(i)
Similarly from P, PT and PB are the tangents drawn to the smaller circle
∴ PT = PB ….(ii)
From (i) and (ii)
PA = PB Hence proved.
Que-7: Two circles touch externally at A. A common tangent touches them at B and C, and another common tangent at A meets the previous common tangent at P, as is shown in figure. Prove that
(i) PB = PC,
(ii) ∠BAC = 90°
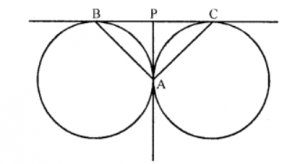
Sol: (i) ∵ Through P, PB and PA are tangents to the first circle
∴ PB = PA ….(i)
Similarly through P, PA and PC are tangents to the second circle
∴ PA = PC ….(ii)
From (i) and (ii)
PB = PC
(ii) In △PAB,
PA = PB (proved)
∴ ZPBA = ZPAB …(iii)
Similarly in △PAC
PA = PC
∴ ∠PCA = ∠PAC ….(iv)
Adding (iii) and (iv)
∠PBA + ∠PCA = ∠PAB + ∠PAC = ∠BAC
But ∠PBA + ∠PCA + ∠BAC = 180° (Sum of angles of a triangle)
∴ ∠BAC + ∠BAC = 180°
⇒ 2 ∠BAC = 180°
⇒ ∠BAC = 180° × (1/2) = 90°
Hence ∠BAC = 90° Hence proved.
Que-8: Two circles touch internally at A. P is any point on the tangent at A. From P, two tangents PB and PC are drawn to the two circles. Prove that PB = PC.
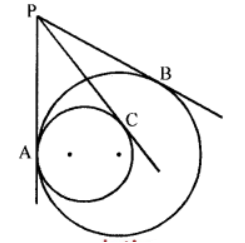
Sol: Given : Two circles touch each other at A externally. Through A, a common tangent is drawn. A point P is taken on the tangents.
Through P, PB and PC two tangents are drawn.
Through P, two tangents PA and PB are drawn to the first circle
∴ PA = PB ….(i)
Again through P, PA and PC are the tangents
drawn to the second circle
∴ PA = PC ….(ii)
From (i) and (ii)
PB = PC Hence proved.
Que-9: From a point P, outside a circle, with centre O, tangents PA and PB are drawn as shown in the figure. Prove that :
(i) ∠AOP = ∠BOP
(ii) OP is the perpendicular bisector of AB.
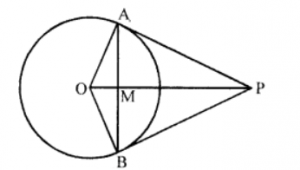
Sol: Given : In the circle with centre O, from a point P outside of it, PA and PB are tangents drawn
OP, OA, OB and AB are joined
(i) In right AOAP and AOBP,
Hyp. OP = OP (common)
Side OA = OB (radii of the same circle)
∴ △OAP = △OBP (RHS axiom)
∴ ∠AOP = ∠BOP (c.p.c.t.)
and ∠APO = ∠BPO (c.p.c.t.)
Now in △AMP and △BMP,
MP = MP (common)
PA = PB (Tangents to the circle)
∠APM = ∠BPM (proved)
∴ △AMP ≅ △BMP (SAS axiom)
∴ AM = BM (c.p.c.t.)
∠AMP = BMP
But ∠AMP + ∠BMP = 180° (Linear pair)
∴ ∠AMP = ∠BMP = 90°
Hence OP is the perpendicular bisector of AB.
Hence proved.
Que-10: Prove that the tangents to a circle at the extremities of any chord make equal angles with the chord.
Sol: Given : In a circle with centre O, AB is the chord. Through A and B tangents PQ and PR are drawn which meet each other at P
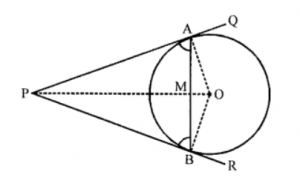
In △OAP and △OBP,
OP = OP (common)
OA = OB (radii of the same circle)
PA = PB (tangents to the circle)
∴ △OAP ≅ △OBP (SSS axiom)
∴ ∠APO = ∠BPO (c.p.c.t.)
Now in △PAM and △PBM,
PM = PM (common)
PA = PB (tangents to the circle)
∠APM = ∠BPM (∠APO = ∠BPO proved)
∴ △PAM ≅ △PBM (SAS axiom)
∴ ∠PAM = ∠PBM
⇒ ∠PAB = ∠PBA Hence proved.
Que-11: In the figure, two circles touch each other externally at C. Prove that the common tangent at C bisects the other two common tangents.
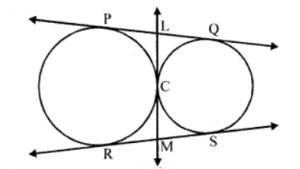
Sol: Given : Two circles with centres O and O’ touch each other externally at C.
PQ and RS are common tangents and a third common tangent from C is drawn which intersects PQ and RS and L and M.
From L, LP and LC are the tangents to the circle.
∴ LP = LC ….(i)
Similarly from L, LQ and LC are two tangents.
∴ LC = LQ ….(ii)
From (i) and (ii)
LP = LC = LQ
∴ L is the midpoint of PQ
Similarly we can prove that
M is the midpoint of RS
Hence LM bisects the tangents PQ and RS
Hence proved.
Que-12: PA and PB are tangents drawn from an external point P to a circle with centre C (See figure). Prove that ∠APB = 2∠CAB.
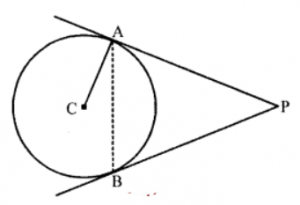
Sol: Given : A circle with centre C. PA and PB are two tangents drawn from P to the circle CA is joined
In △APB,
AP = BP (tangents to the circle from P)
∴ ∠PAB = ∠PBA (opposite angles to equal sides)
But vPAB + ∠PBA + ∠APB = 180° (Sum of angles of a triangle)
⇒ ∠PAB + ∠PAB + ∠APB = 180°
⇒ ∠APB = 180°- 2∠PAB
But ∠PAB = ∠CAP – ∠CAB
= 90° – ∠CAB (∵ CA ⊥ PA)
∴ ∠APB = 180° – 2 (90° – ∠CAB)
⇒ ∠APB = 180° – 180° + 2∠CAB
⇒ ∠APB = 2 ∠CAB
Hence proved.
–: End of Circles Class 10 OP Malhotra Exe-14D ICSE Maths Solutions Ch-14 :–
Return to :- OP Malhotra S Chand Solutions for ICSE Class-10 Maths
Thanks
Please Share with Your Friends


