Circles Class 10 OP Malhotra Exe-14E ICSE Maths Solutions Ch-14 questions as latest prescribe guideline for upcoming exam. In this article you would learn to solve problems on Segments of a Chord. Visit official Website CISCE for detail information about ICSE Board Class-10 Mathematics.

Circles Class 10 OP Malhotra Exe-14E ICSE Maths Solutions Ch-14
| Board | ICSE |
| Publications | S Chand |
| Subject | Maths |
| Class | 10th |
| Chapter-14 | Circles |
| Writer | OP Malhotra |
| Exe-14E | Segments of a Chord |
| Edition | 2024-2025 |
Chord Properties
- Definition: A chord is a straight line segment with both endpoints lying on the circumference of a circle.
- Segments of the chord: When two chords intersect in the interior of a circle, each chord is divided into two segments that are called segments of the chord
- Bisecting property: A line drawn from the center of a circle perpendicular to a chord will bisect the chord.
- Equal chords and angles: Equal chords subtend equal angles at the center of the circle.
- Distance from center: Chords that are the same distance from the center of the circle are equal in length.
- Major and minor segments: A chord divides a circle into two segments, called a major segment and a minor segment.
- Diameter as the longest chord: The longest chord of a circle is the diameter.
- If two chords intersect in the interior of a circle, then the product of the lengths of the segments of one chord is equal to the product of the lengths of the segments of the other chord
- If a chord and a tangent intersect externally, then the product of the lengths of the segments of the chord is equal to the square of the length of the tangent from the point of contact to the point of intersection
Exercise- 14E (Segments of a Chord)
Circles Class 10 OP Malhotra Exe-14E ICSE Maths Solutions Ch-14
Que-1: In fig., if AB and CD are two chords of a circle intersecting at a point P inside the circle such that
(i) AP = 8 cm, CP = 6 cm and PD = 4 cm, find PB.
(ii) AB = 12 cm, AP = 2 cm and PD = 4 cm, find CP.
(iii) AP = 6 cm, PB = 5 cm and CD = 13 cm, find CP.
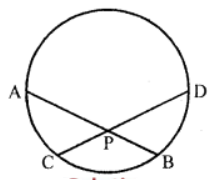
Sol: ∵ AB and CD are two chords which intersect
at P inside the circle
∴ AP × PB = CP × PD
(i) Now AP = 8 cm, CP = 6 cm and PD = 4 cm
∴ 8 × PB = 6 × 4 ⇒ PB = (6×4)/8 cm
∴ PB = 3 cm
(ii) AB = 12 cm, AP = 2 cm and PD = 4 cm
∴ PB = AB – AP = 12 – 2 = 10 cm
Now AP × PB = CP × PD
⇒ 2 × 10 = CP × 4 ⇒ CP = (2×10)/4 = 5 cm
∴ CP = 5 cm
(iii) AP = 6 cm, PB = 5 cm and CD = 13 cm
Let CP = x, then PD = CD – CP
= (13 – x) cm
Now AP × PB = CP × PD
⇒ 6 × 5 = x(13 – x) ⇒ 30 = 13 x – x2
⇒ x2 – 13x + 30 = 0
⇒ x2 – 10x – 3x + 30 = 0
⇒ x(x – 10) – 3 (x – 10) = 0
⇒ (x- 10)(x – 3) = 0
Either x – 10 = 0, then x = 10
or x – 3 = 0, then x = 3
CP = 10 cm or 3 cm
Que-2: In figure, if AB and CD are two chords of a circle which when produced meet at a point P such that
(i) PA = 10 cm, PB = 4 cm and PC = 8 cm, find PD.
(ii) PC = 15 cm, CD = 7 cm and PA = 12 cm, find AB.
(iii) PA = 16 cm, PC = 10 cm and PD = 8 cm, find AB.
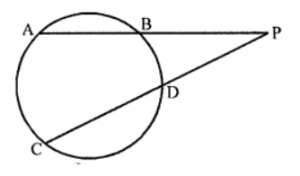
Sol: ∵ Chords AB and CD of a circle intersect each other at P outside the circle
∴ AP × PB = CP × PD
(i) PA = 10 cm, PB = 4 cm and PC = 8 cm
Now AP × PB = CP × PD
⇒ 10 × 4 = 8 × PD
⇒ PD= (10×4)/8 = 5
∴ PD = 5 cm
(ii) PC = 15 cm, CD = 7 cm and PA = 12 cm
PD = CP – CD = 15 – 7 = 8 cm
Now PA × PB = PC × PD
12 × PB = 15 × 8
⇒ PB = (15×8)/12 = 10 cm
∴ AB = PA – PB = 12 – 10 = 2 cm
(iii) PA = 16 cm, PC = 10 cm and PD = 8 cm
Now PA × PB = PC × PD
⇒ 16 × PB = 10 × 8
⇒ PB = (10×8)/16 = 5
∴ AB = PA – PB = 16 – 5 = 11 cm
Que-3: (i) In figure, if PT is a tangent to the circle, PB = 4 cm and AB = 12 cm, then PT = …….cm. (ii) From an external point P, the tangent PT and a secant PAB are drawn. If PA = 9.6 cm and PB = 2.4 cm, determine PT.
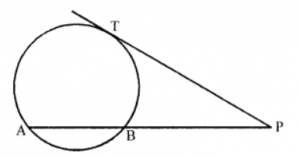
Sol: (i) In the figure, PT is tangent and PBA is a secant to the circle PB = 4 cm, AB = 12 cm
∴ PA = PB + AB = 4 + 12 = 16 cm
∴ PT2 = PA × PB
= 16 × 4 = 64 = (8)2
∴ PT = 8 cm
(ii) From an external point P, PT is the tangent to the circle and PAB is a secant
and PA = 9.6 cm, PB = 2.4 cm
Now PT2 = PA × PB = 9.6 × 2.4
= 23.04 = (4.8)2
∴ PT = 4.8 cm
Que-4: The angle A of the triangle ABC is a right angle. The circle on AC as diameter cuts BC at D. If BD = 9, and DC = 7, calculate the length of AB.
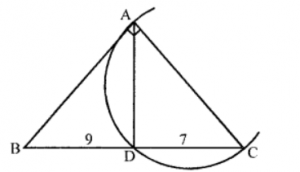
Sol: In △ABC, ∠A = 90°
A circle is drawn on AC as diameter which intersects BC at D
AD is joined
BD = 9 and DC = 7
We see that in the circle AB is the tangent at A and BDC is the secant of the circle
∴ AB2 = BD × BC
= 9 × 16 {∵ BC = BD + DC = 9 + 7 = 16}
= 144 = (12)2
∴ AB = 12
Que-5: In △ABC, AB = 9, AC = 12, F is the mid-point of AC; the circle BFC intersects AB at E; find BE.
Sol: Steps of construction :
(i) Draw a line segment AB = 9
At A draw ∠BAC = 90° and cut off AC = 12
(ii) Join BC. Take F as midpoint of AC.
(iii) Now draw perpendicular bisector of FC and BC intersecting each other at O.
(iv) With centre O, and radius OC draw a circle with passes through B, F and C and intersects AB at E on measuring BE = 1.
Que-6: In △ABC, ∠BAC = 90°, AB = 4, AC = 3, AD is an altitude, find BD.
Sol: ABC ABC is a right angled triangle in which ∠A = 90°,
AD ⊥ BC
AB = 4, AC = 3
∴ BC2 = AB2+AC2 (Pythagoras theorem)
= (4)2 + (3)2 = 16 + 9 = 25 = (5)2
∴ BC = 5
Let BD = x, then DC = 5 – x
Now AB2 = BD × BC
(4)2 = x × 5 ⇒16 = 5x ⇒ x = 16/5 = 3*(1/5)
∴ BD = 3*(1/5).
Que-7: From the external point P, PA is a tangent to the circle at A. PBC is a secant intersecting the circle at B and C. What is the power of P with respect to the circle if PA = 7 ? What is the value of PB.PC ?
Sol: From a point P,
Outside the circle PA is tangent and PBC is the secant PA = 7
Power of P with respect to the circle
= PA2 = (7)2 = 49
∵ PA is tangent and PBC is the secant
∴ PA2 = PB × PC => 49 = PB × PC
Hence PB.PC = 49
Que-8: In figure, ABC is a triangle inscribed in a circle. AB =AC = 10 cm, BC = 16 cm. The chord AE is at right angles to the chord BC at D. Calculate DE and the radius of the circle.
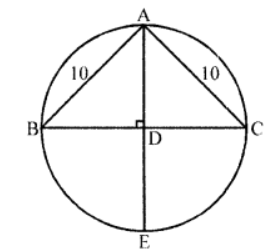
Sol: △ABC in which AB = AC = 10 cm and BC = 16 cm, is inscribed in a circle AE is a chord which is at right angle to BC at D
In △ABC,
AB = AC and AD ⊥ BC
∴ BD = DC = 16/2 = 8 cm
Now in right △ABD,
AB² = BD² + AD² ⇒ (10)² = (8)² + AD²
⇒ 100 = 64 + AD²
⇒ AD² = 100 – 64 = 36 = (6)²
∴ AD = 6
Now two chords AE and BC intersect each other at D
BD × DC = AD × DE
⇒ 8 × 8 = 6 × DE ⇒ DE = (8×8)/6 = 64/6 = 32/3
∴ DE = 32/3 = 10*(2/3) cm
Now AE = AD + DE = 6 + {10*(2/3)} = 16*(2/3) cm
∴Radius = 1/3 AE (∵ AE is diameter)
= 1/3 × {16*(2/3)} = 8*(1/3) cm
Que-9: In figure, XY is a tangent to the circle with centre O. XCD is a secant. Calculate r, the radius of the circle.

Sol: In the figure, XY is a tangent to the circle with centre O. XCD is a secant
ON ⊥ DX
Join OC and join OB
CX = 4 and XB = 6
∵XB is tangent and XCD is the secant
Let CD = x
∴ XB2 = XC × XD ⇒ (6)2 = 4 (4 + x)
= 4(4 + x) = 36 ⇒ 4 + x = 36/4 = 9
x = 9 – 4 = 5
∴ CD = 5
∵ ON ⊥ CD
∴ CN = ND = 5/2
∴ Radius OB = NX = CN + XC
= (5/2) + 4 = 6*(1/2) cm
Que-10: In figure, O is the centre of the circle. If
(i) AX = 5 cm, XD = 7 cm, CX = 10 cm; find BX.
(ii) OA = 6 cm, BX = 5 cm, OX = 4 cm; find XC.
(iii) CD = 2 cm, DP = 6 cm, BP = 3 cm; find AB.
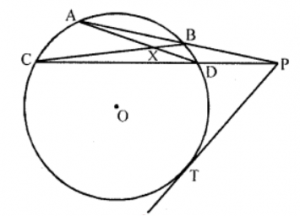
Sol: In the figure, PBA, PDC are the secants PT is the tangents to the circle with centre O AD and BC are joined which intersect each other at X
(i) AX = 5 cm, XD = 7 cm, CX = 10 cm
∵ Two chords AD and BC intersect each other at X
∴ AX.XD = CX.XB
⇒ 5 × 7 = 10 × XB
⇒ XB = (5×7)/10 = 7/2 = 3.5 cm
(ii) OA = 6 cm, BX = 5 cm, OX = 4 cm
Join OA, OX and produce it to both sides meeting the circle at P and Q
OA = OP = OQ (radii)
XP = OP – OX = OA – OX = 6 – 4 = 2 cm
XQ = OX + OQ = OX + OA = 6 + 4 = 10 cm
∵ Chord BC and PQ intersect each other at X
∴ XC × 5 = 2 × 10 ⇒ XC = (2×10)/5 = 4
∴ XC = 4 cm
(iii) CD = 2 cm, DP = 6 cm, BP = 3 cm
Let AB = x
∵ Chords AB and CD intersect each other at P outside the circle
∴ PA × PB = PC × PD
(x + 3) × 3 = (2 + 6) × 6
(x + 3) × 3 = 8 × 6 ⇒ x + 3 = (8×6)/3 = 16
x = 16 – 3 = 13
∴ AB = 13 cm
Que-11: In figure, two circles intersect each other at the points P and Q. If AB and AC are the tangents to the two circles from a point A on QP produced, show that AB = AC.
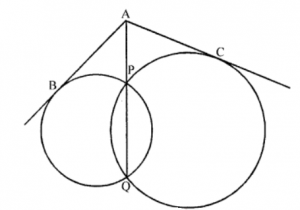
Sol: Given : Two circles intersect each other at P and Q
AB and AC are the tangents on QP produced from A
AB is the tangent and APQ is a secant
∴ AB2 = AP × AQ …(i)
Similarly AC is the tangent and APQ is the secant
∴ AC2 =AP × AQ …(ii)
From (i) and (ii)
AB2 = AC2
⇒ AB = AC
Hence proved.
Que-12: In figure, AB is any chord of a circle with centre O and P is any point on this chord. A perpendicular drawn through P on OP cuts the circumference in X. Prove that AP.PB = PX2.

Sol: Given : In a circle AB is a chord of a circle with centre O
P is any point on AB and PX ⊥ OP
XY is a chord and OP ⊥ XY
∴ P is the midpoint of XY
∴ PX = PY
Now chord AB and XY intersect each other at P
∴ AP × PB = XP × PY
⇒ AP.PB = XP × XP (∵ XP = PY)
⇒ AP.PB = XP2 or AP.PB = PX2
Hence proved.
Que-13: In figure, the two circles intersects at S and T, and STP, BSC, BAP and CDP are st. lines. Prove that (i) the quad. PATD is cyclic; (ii) PA.PB = PD.PC.
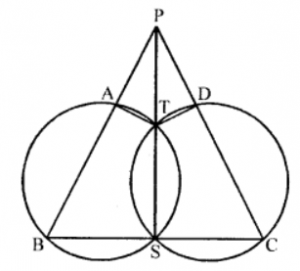
Sol: (i) ∵ ABST is a cyclic quad.
∴ Ext. ∠ATP = Int. opp. ∠B (i)
Similarly in cyclic quad. CDTS,
Ext. ∠DTP = ∠C ….(ii)
Adding (i) and (ii)
∠ATP + ∠DTP = ∠B + ∠C ….(iii)
But in △PBC,
∠BPC + ∠B + ∠C= 180° (Sum of angles of a triangle)
⇒ ∠B + ∠C = 180° – ∠BPC From (iii)
∠ATP + ∠DTP =180°- ∠BPC
⇒ ∠ATD + ∠BPC = 180°
But these are sum of opposite angles of quad. PATD
∴ Quad. PATD is a cyclic quad.,
(ii) ∵ Chords BA and ST intersect at P outside the circle
∴ PA × PB = PT × PS ….(i)
Similarly CD and ST chords meet at P
∴ PD × PC = PT × PS ….(ii)
From (i) and (ii)
PA.PB = PD.PC Hence proved.
Que-14: Two circles intersect at A. Chords PAQ and RAS are drawn through A, each passing through the centre of one of the two circles and terminated by the circumference. Prove PA.AQ = RA.AS.
Sol: In △APR and △ASQ,
∠P = ∠S (each 90° being in a semicircle)
∠PAR = ∠QAS (Vertically opposite angles)
∴ △APR ~ △ASQ (AA axiom)
∴ PA/AS = RA/AQ
∴ PA.AQ = RA.AS (By cross multiplication)
Hence proved.
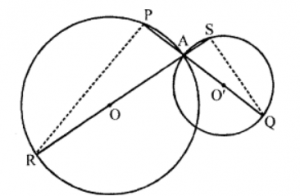
Que-15: Two circles intersect at points A and B. From a point P on the common chord BA produced, secants PCD and PEH are drawn one to each circle. Prove that the points C, D, H, E are concyclic.
Sol: DC and BA are chords which intersect at P outside the first circle
∴ PC × PD = PA × PB ….(i)
Similarly, chords BA and HE intersect each other at P outside the second circle
∴ PA × PB = PE × PH ….(ii)
From (i) and (ii)
PC × PD = PE × PH
But there are two chords DC and HE which meet at P outside the circle
∴ C, D, H and E are concyclic Hence proved.
Que-16: In figure, PB = BT and PT is tangent to the circle, then prove that (i) △PTC is isosceles (ii) PB.PC = TC2
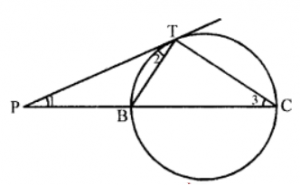
Sol: (i) In △PBT,
PB = BT (given)
∴ ∠1 = ∠2 ….(i)
But PT is tangent and BT is the chord of the circle
∴ ∠2 = ∠3 ….(ii)
(Angle in the alternate segment) From (0 and (ii)
∠1 = ∠3
∴ In ATPC,
TP = TC (Sides opposite to equal angles)
∴ △PTC is an isosceles triangle
(ii) ∵ PT is tangent and PBC is secant of the circle
∴ PT2 = PB.PC
⇒ PB.PC = PT2 = TC2
[∵ PT = TC proved in (i)]
⇒ PB.PC = TC2
Hence proved.
–: End of Circles Class 10 OP Malhotra Exe-14E ICSE Maths Solutions Ch-14 questions :–
Return to :- OP Malhotra S Chand Solutions for ICSE Class-10 Maths
Thanks
Please Share with Your Friends