Circles Class 10 OP Malhotra Exe-14F ICSE Maths Solutions Ch-14 questions as latest prescribe guideline for upcoming exam. In this article you would learn to solve problems on Angles in Alternate Segment. Visit official Website CISCE for detail information about ICSE Board Class-10 Mathematics.

Circles Class 10 OP Malhotra Exe-14F ICSE Maths Solutions Ch-14
| Board | ICSE |
| Publications | S Chand |
| Subject | Maths |
| Class | 10th |
| Chapter-14 | Circles |
| Writer | OP Malhotra |
| Exe-14F | Angles in Alternate Segment |
| Edition | 2024-2025 |
Angles in Alternate Segment
the angle between a chord and a tangent through one of the end points of the chord is equal to the angle in the alternate segment
Exercise- 14F (Angles in Alternate Segment)
Circles Class 10 OP Malhotra Exe-14F ICSE Maths Solutions Ch-14
Que-1: In figure, PT is a tangent to a circle. If ∠BTA = 45° and ∠PTB = 75°, find ∠ABT.
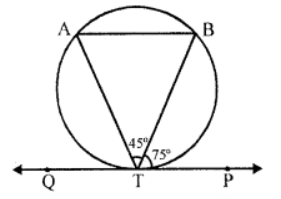
Sol: In the figure, PQ is the tangent to the circle at T
∠BTP = 75° and ∠ATB = 45°
But ∠QTA + ∠ATB + ∠BTP = 180° (Angles of a line)
∠QTA + 45° + 75° = 180° ⇒ ∠QTA + 120° = 180°
⇒ ∠QTA = 180° – 120° = 60°
Now QTP is the tangent and TA is the chord
∴ ∠QTA = ∠ABT (Angle in the alternate segment)
⇒ ∠ABT = 60°
Que-2: In figure, TAS is a tangent to the circle, with centre O, at the point A. If ∠OBA = 32°, find the values of x and y.
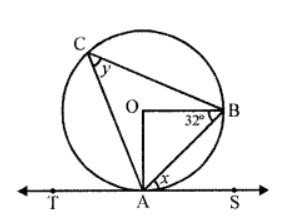
Sol: In the figure, a circle with centre O
TAS is a tangent to the circle at A
AB, AC and BC are chords of the circle
∠OBA = 32°
In △OAB,
OA = OB (radii of the same circle)
∴ ∠OAB = ∠OBA = 32°
In △AOB,
∠AOB + ∠OAB + ∠OBA = 180° (Sum of angles of a triangle)
⇒ ∠AOB + 32° + 32° = 180°
⇒ ∠AOB + 64° = 180°
⇒ ∠AOB = 180° – 64° = 116°
Now arc AB subtends ∠AOB at the centre and ∠ACB at the remaining part of the circle
∴ ∠AOB = 2 ∠ACB
⇒ 116° = 2y ⇒ y = 116°/2 = 58°
But ST is the tangent and AB is the chord
∴ ∠BAS = ∠ACB
⇒ x = y ⇒ x = y = 58°
Que-3: In figure, KLMN is a cyclic quadrilateral and PQ is a tangent to the circle at K. If LN is a diameter of the circle, ∠KLN = 30° and ∠MNL = 60°, determine
(i) ∠QKN,
(ii) ∠PKL,
(iii) ∠MLK.
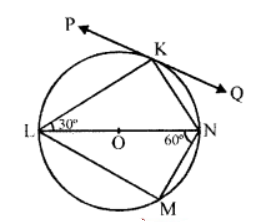
Sol: In the circle with centre O,
LN is the diameter
PQ is a tangent to the circle at K
∠KLN = 30° and ∠MNL = 60°
In △LKN,
∠LKN = 90° (Angle in a semicircle)
∠KLN = 30°
∴ ∠KNL = 90° – 30° = 60°
(i) Now PQ is tangent and KN is chord of the circle at K
∴ ∠QKN = ∠KLN = 30° (Angle in the alternate segment)
(ii) Again PQ is tangent and KL is the chord
∴ ∠PKL = ∠KNL = 60°
(iii) In cyclic quad LMNK,
∠KNM + ∠KLM = 180° (sum of opposite angles)
⇒ ∠KNL + ∠LNM + ∠MLK = 180°
⇒ 60° + 60° + ∠MLK = 180°
⇒ ∠MLK + 120° = 180°
⇒ ∠MLK = 180°- 120°
⇒ ∠MLK = 60°
Que-4 In figure, AT is a tangent to the circle. If ∠ABC = 50° and AC = BC, find ∠BAT.
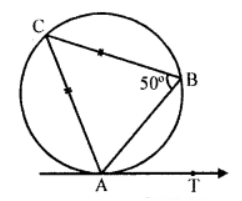
Sol: In the figure, AT is the tangent to the circle and ZABC = 50°
AC = BC
∴ ∠BAC = ∠ABC = 50° (opposite of equal sides)
But ∠ACB + ∠BAC + ∠ABC = 180° (sum of angles of a triangle)
ZACB+ 50°+ 50°= 180°
⇒ ∠ACB + 100°= 180°
⇒ ∠ACB = 180° – 100° = 80°
∵ AT is the tangent and AB is chord
∠BAT = ∠ACB = 80° (Angles in the alternate segment)
Que-5: In figure, O is the centre of the circumcircle of △XYZ. Tangents at X and Y intersects at T. Given, ∠XTY = 80° and ∠XOZ = 140°. Calculate ∠ZXY.
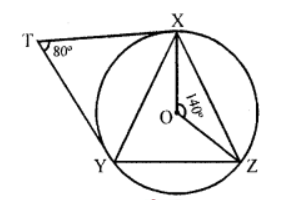
Sol: In the figure, O is the centre of circumcircle of △XYZ.
Tangents at X and Y are drawn to meet at T
∠XTY = 80° and ∠XOZ = 140°
Join OY
XT and YT are tangents to the circle
∴ ∠XTY + ∠XOY = 180° (Angles are supplementary)
⇒ 80° + ∠XOY = 180°
⇒ ∠XOY =180° – 80° = 100°
But ∠XOY + ∠YOZ + ∠ZOX = 360° (Angles at a point)
⇒ 100° +∠YOZ + 140° = 360°
⇒ ∠YOZ + 240° = 360°
∠YOZ = 360° – 240° = 120°
Now arc YZ subtends ∠YOZ at the centre and ∠ZXY at the remaining part of the circle
∴ ∠YOZ = 2 ∠ZXY
⇒ ∠ZXY = (1/2) ∠YOZ = (1/2) × 120° = 60°
Que-6: In figure, O is the centre of the circle and AB is a chord of the circle. Line QBS is a tangent to the circle at B. If ∠AOB = 110°, find ∠APB and ∠ABQ.
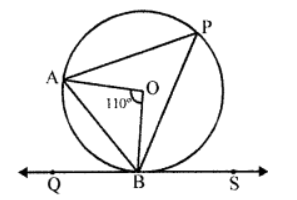
Sol: O is the centre of the circle, AB is the chord and QBS is the tangent to the circle at B
∠AOB = 110°
Arc AB subtends ∠AOB at the centre and ∠APB at the remaining part of the circle
∴ ∠AOB = 2 ∠APB ⇒ ∠APB = (1/2) ∠AOB
⇒ ∠APB = (1/2) × 110° = 55°
Now QBS is the tangent and AB is the chord
∴ ∠ABQ = ∠APB = 55°
Hence ∠APB = ∠ABQ = 55°
Que-7: In figure, AB is a diameter and AC is a chord of a circle such that ∠BAC = 30°. The tangent at C intersects AB produced at D. Prove that BC = BD.
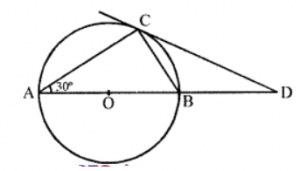
Sol: Given : In a circle with centre O and
AB is its diameter
At C, a tangent is drawn to the circle which
meet AB on producing at D
∠BAC = 30°
CD is tangent and CB is chord
∴ ∠DCB = ∠BAC = 30° (Angles in the alternate segment)
In △ABC,
∠ACB = 90° (Angle in a semicircle)
∴ ∠BAC + ∠CBA = 90°
⇒ 30° + ∠CBA = 90°
⇒ ∠CBA = 90°- 30° = 60°
Now in △BCD
Ext. ∠CBA = ∠BCD + ∠BDC
⇒ 60° = 30° + ∠BDC ⇒ ∠BDC = 60° – 30° = 30°
∵ ∠BCD = ∠BDC = 30°
BC = BD (Sides opposite to equal angles)
Hence proved.
Que-8: In figure, DE is a tangent to the circumcircle of △ABC at the vertex A such that DE || BC. Show that AB = AC.
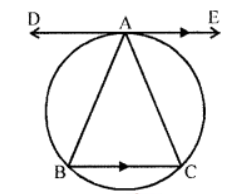
Sol: In a circle, DE is a tangent at A to the circumcircle of △ABC in which DE || BC
DE is the tangent and AB is the chord of the circle
∴ ∠DAB = ∠ACB ….(i) (Angles in the alternate segment)
But DE || BC
∴ ∠DAB = ∠ABC ….(ii) (Alternate angles)
From (i) and (ii)
∠ACB = ∠ABC
∴ AB=AC (Sides opposite equal angles) Hence proved.
Que-9: In figure, two circles intersect in B and C. Lines ABD and ACE are drawn to meet the second circle at points D and E, AF is a tangent at A. Prove that AF || DE.
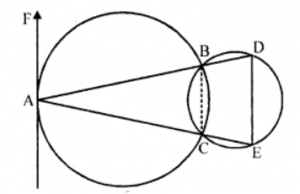
Sol: Given : Two circles intersect each other at B and C. Lines ABD and ACE are drawn to meet the smaller circle at D and E respectively. AF is the tangent to the first circle at A
AF is the tangent and AB is the chord of the first circle
∴ ∠BAF = ∠ACB ….(i) (Angles in the alternate segment)
In cyclic quadrilateral BCED,
Ext. ∠ACB = Int. opp. ∠BDE ….(ii)
From (i) and (ii)
∠BAF = ∠BDE
But these are alternate angles
∴ AF || DE
Hence proved.
Que-10: In the figure, CD is the tangent line at C to the circumcircle of △ABC intersecting AB produced in D. Show that △DBC ~ △DCA.
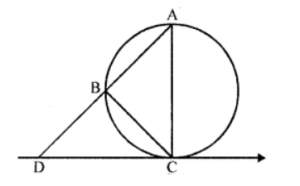
Sol: A circumcircle of △ABC, a tangent DC is drawn at C and AB is produced to meet the tangent at D
CD is tangent and BC is the chord of the circle
∴ ∠BCD = ∠BAC (Angles in the alternate segment)
Now in △DBC and △DCA,
∠D = ∠D (common)
∠BCD = ∠BAC or ∠DAC (proved)
∴ △DBC ~ △DCA
Hence proved.
–: End of Circles Class 10 OP Malhotra Exe-14F ICSE Maths Solutions / Answer of Ch-14 :–
Return to :- OP Malhotra S Chand Solutions for ICSE Class-10 Maths
Thanks
Please Share with Your Friends