Circles Class 10 OP Malhotra Exe-14G ICSE Maths Solutions Ch-14 Questions as latest prescribe guideline for upcoming exam. In this article you would learn How to Construct Tangents. Visit official Website CISCE for detail information about ICSE Board Class-10 Mathematics.
Circles Class 10 OP Malhotra Exe-14G ICSE Maths Solutions Ch-14
| Board | ICSE |
| Publications | S Chand |
| Subject | Maths |
| Class | 10th |
| Chapter-14 | Circles |
| Writer | OP Malhotra |
| Exe-14G | How to Construct Tangents |
| Edition | 2024-2025 |
How to Construct Tangents if Centre is Given
Step 1: From the center of the circle, draw a straight line through the given point on the edge or outside the circle. Make sure the line extends significantly beyond the edge of the circle.
Step 2: Identify the intersection between the line you just drew and the circle. Then, draw two points on the line that are equidistant from the intersection point, one on the inside and one on the outside of the circle.
Step 3: At each of the two equidistant points and using a compass, draw a circle around each point. The two circles must be the same size and the radius of the circles must be larger than the distance from the point to the intersection of the line and the circle.
Step 4: Identify the two places where the circles intersect and connect them with a line. This line will be perfectly tangent to the circle.
How to Construct Tangents if Centre is Not Given
To construct tangents to a circle when the center is not given, you can draw two non-parallel chords within the circle, then construct the perpendicular bisectors of those chords; the intersection point of these bisectors will be the center of the circle, allowing you to then draw tangents from any point on the circle using the above tangent construction method
How to Construct the Circumcircle of a Triangle
- Draw the triangle
- Choose two sides of the triangle
- Construct the perpendicular bisectors of the chosen sides
- Find the point where the perpendicular bisectors intersect
- This point is the center of the circumcircle
- Place a compass on the center point
- Adjust the compass to reach any corner of the triangle
- Draw the circumcircle
How to Construct the Inscribed circle of a Triangle
- Draw the angle bisectors of any two angles of the triangle.
- where they intersect is the center of the inscribed circle called incenter.
- Then, draw a perpendicular from the incenter to any side of the triangle.
- The length of this perpendicular is the radius.
- Taking incenter as the center and the radius to draw the inscribed circle.
- If all thing ok then it will just touch all three sides of the triangle.
Exercise- 14G (How to Construct Tangents)
Circles Class 10 OP Malhotra Exe-14G ICSE Maths Solutions Ch-14
Que-1: Using ruler and compasses only construct the tangents to the given circle from the point P. Measure the length of each one of them.
Sol: Steps of construction :
(i) Draw a circle with centre O and a suitable radius.
(ii) Take of point P outside the circle.
(iii) Join OP and take its midpoint M.
(iv) With centre M and diameter OP, draw a circle which intersects the given circle at T and S.
(v) Join PT and PS.
PT and PS are required tangents to the circle on measuring PT = PS = 5.5 cm. (approx)
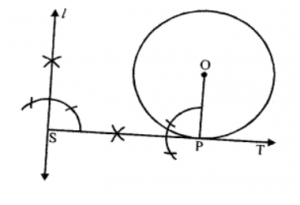
Que-2: Draw a tangent to a circle which may be perpendicular to a given line.
Sol: Steps of construction :
(i) Draw a circle with centre O and with a suitable radius.
(ii) Take a point P on it and join OP.
(iii) At P, draw a perpendicular to OP which meet a given line l at S.
Then ST is the required tangent.
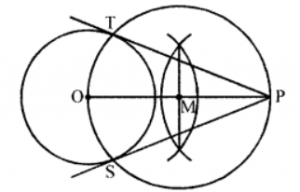
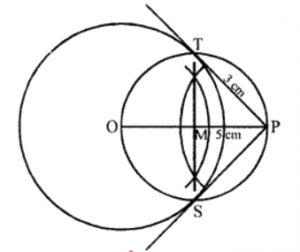
Que-3: Using ruler and compasses only, draw tangents to a circle of radius 4 cm from a point 5 cm from the centre. What is the length of each of them ?
Sol: Steps of construction :
(i) Draw a circle with centre O and radius 4 cm.
(ii) Take a point P such that OP = 5 cm.
(iii) Draw its bisector which bisects OP at M.
(iv) With centre M and radius MP draw a circle intersecting the given circle at T and S.
(v) Join PT and PS.
PT and PS are the required tangents to the circle on measuring each of them PT = PS = 3 cm.
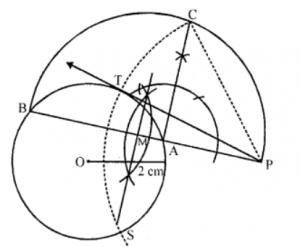
Que-4: Draw a circle of radius 2 cm and construct a tangent to it from an external point without using the centre.
Sol: Steps of construction :
(i) Draw a circle with centre O and radius 2 cm.
(ii) Take a point P outside the circle.
(iii) From P draw a straight line which intersects the circle at A and B.
(iv) With BP as diameter draw a semicircle.
(v) At A, draw a perpendicular which meets the semicircle at C.
(vi) With centre P and radius PC, draw an arc which intersects the given circle at T and S.
(vii) Join PT.
PT is the required tangent.
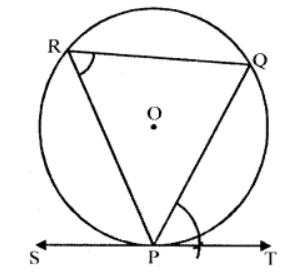
Que-5: Through a given point on the circumference of a circle, draw a tangent to the circle without using its centre.
Sol: Steps of construction :
(i) Draw a circle with centre O and some suitable radius.
(ii) Take a point P on it.
(iii) Take two more points Q and R on the remaining part of the circle and joined PQ, QR and RP.
(iv) Draw an angle ∠QPT equal to ∠R and produce the line TP to S.
Then SPT is the required tangent to the circle.
Que-6: Draw two tangents, inclined at an angle of 60° to each other, to a circle with radius of 3 cm. Measure the length of one of the tangents and verify by calculation.
Sol: Steps of construction :
(i) Draw a circle with centre O and a suitable radius.
(ii) Draw a radius OS and on PS, draw an angle ∠SOT of 180°- 60°= 120°.
(iii) At S and T, draw lines making 90° each. Which intersect each other at P.
Then PT and SP are the required tangents making an angle of 60° with each other at P on measuring them each one of them is 4.5 cm.
Calculation :
Here radius of the circle (r) = 3 cm
and distance of OP = 5.3 cm
In right △OPT,
PT2 = OP2 – OT2 = (5.3)2 – (3)2
= 28.09 – 9 = 19.09 = (4.37)2
∴ PT = 4.37 cm
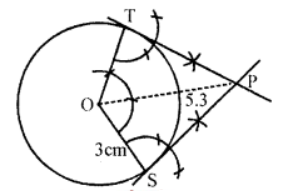
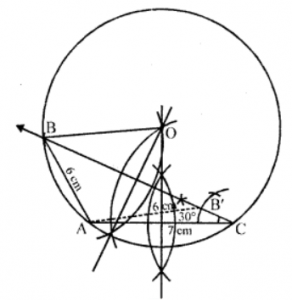
Que-7: Using ruler and compasses only construct a triangle ABC having given c = 6 cm, b = 7 cm and ∠C = 30°. Measure side a. Draw carefully the circumcircle of the triangle. Measure its radius. (Two triangles are possible).
Sol: Steps of construction :
(i) Draw a line segment AC = 7 cm (b = 7 cm)
(ii) At C, draw a ray CX making an angle of 30°.
(iii) With centre A and radius 6 cm (c = 6 cm), draw arc which intersects CX at B and B’.
(iv) JoinAB andAB’.
Then two triangles are possible, △ABC and △AB’C in which a = 1.3 cm or 11.3 cm.
(v) Now draw the perpendicular bisectors of AC and BC which intersect each other at O.
(vi) With centre O and radius equal to OB, draw a circle which passes through A, B and C. Then this is the required circumcircle of the △ABC.
On measuring its radius = 6.5 cm (approx).
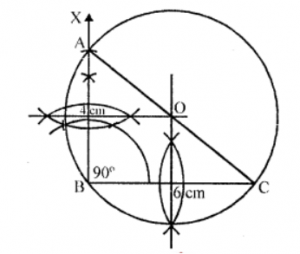
Que-8: Using ruler and compasses only draw a triangle ABC such that AB = 4 cm, BC = 6 cm and ∠B = 90°. Draw the circum-scribed circle of the triangle and state its radius.
Sol: Steps of construction :
(i) Draw a line segment BC = 6 cm.
(ii) At B, draw a ray BX making an angle of 90° and cut off BA = 4 cm.
(iii) Join AC.
(iv) Now draw the perpendicular bisectors of AB and BC intersecting each other at O.
(v) With centre O and radius OA, draw a circle which will pass through A, B and C.
This is required circumcircle of △ABC whose radius is (1/2) AC = 3.6 cm.
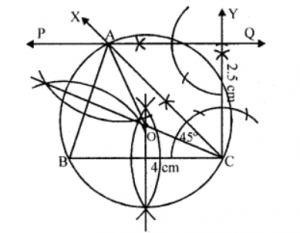
Que-9: Using ruler and compasses only construct a triangle ABC in which BC = 4 cm. ∠ACB = 45° and the perp. from A on BC is 2.5 cm. Draw a circle circumscribing a triangle ABC and measure its radius.
Sol: Steps of construction :
(i) Draw a line segment BC = 4 cm.
(ii) At C, draw a ray CX making an angle of 45° and CY making an angle of 90°.
(iii) Cut off CQ = 2.5 cm.
(iv) From Q, draw a line PQ parallel to BC. Which meets CX at A.
(v) JoinAB.
(vi) Draw the perpendicular bisector of AB and BC which intersect each other at O.
(vii) With centre O and radius OA, draw a circle which will pass through A, B and C.
This is the required circumcircle of △ABC whose radius OA = 2.1 cm (approx).
Que-10: Answer true or false:
The centre of the circumcircle of a right-angled triangle is the mid-point of its hypotenuse.
Sol: It is true.
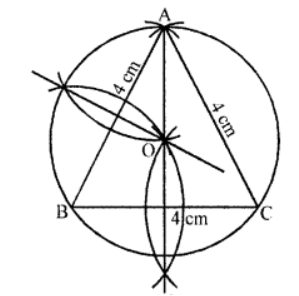
Que-11: Draw an equilateral triangle of side 4 cm. Draw the circumcircle of it.
Sol: Steps of construction :
(i) Draw a line segment BC = 4 cm.
(ii) With centres B and C and radius 4 cm, draw arcs which intersect each other at A.
(iii) Join AB and AC.
Then △ABC is an equilateral triangle.
(iv) Draw the perpendicular bisectors of sides AB and BC which intersect each other at O.
(v) With centre O and radius OA, draw a circle which will pass through A, B, C.
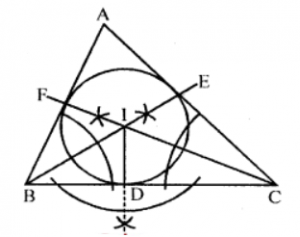
Que-12: Using ruler and compasses only inscribe a circle in the given triangle and measure its radius.
Sol: Steps of construction :
(i) Draw the given △ABC.
(ii) Draw the angle bisectors of ∠B and ∠C which intersect each other at I.
(iii) From I, draw a perpendicular ID on BC.
(iv) With centre I and radius ID, draw a circle which touches the sides of the triangle ABC at D, E and F.
On measuring the radius ID = 1.4 cm (approx).
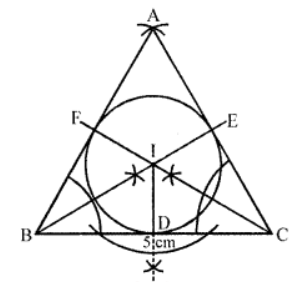
Que-13: Using ruler and compasses only, draw an equilateral triangle of side 5 cm and draw its inscribed circle. Measure the radius of the circle.
Sol: Steps of construction :
(i) Draw a line segment BC = 5 cm.
(ii) With centres B and C and radius 5 cm, draw arcs intersecting each other at A.
(iii) Join AB and AC.
△ABC is an equilateral triangle.
(iv) Draw the angle bisectors of ∠B and ∠C which intersect each other at 1.
(v) From I, draw ID ⊥ BC.
(VJ) With centre I and radius ID, draw a circle which will touch the sides of △ABC at D, E and F.
On measuring, the radius ID = 1.5 cm (approx).
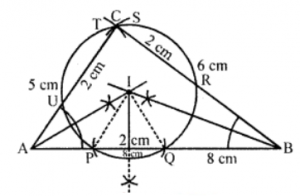
Que-14: (a) Using ruler and compasses only, construct a triangle ABC in which AB = 8 cm, BC = 6 cm and CA = 5 cm.
(b) Find its in-centre and mark it I.
(c) With I as centre, draw a circle which will cut off 2 cm chords from each side of the triangle. What is the length of the radius of this circle ?
Sol: (a) (i) Draw a line segment AB = 8 cm.
(ii) With centre A and radius 5 cm and with centre B and radius 6 cm, draw arcs which intersect each other at C.
(iii) Join AC and BC.
△ABC is the required triangle.
(b) (i) Draw the bisector of ∠A and ∠B which intersect each other at I. I is the incentre of the in circle.
(c) (i) From I, draw IL ⊥ AB.
(ii) From L, cut off LP = LQ = 1 cm so that PQ = 2 cm.
(iii) With centre I and radius IP, draw a circle which intersects BC at R and S and CA at T and U.
Then chords PQ = RS = TU = 2 cm.
Que-15: Inscribe a circle in a regular hexagon of side 3.2 cm.
Sol: Steps of construction :
(i) Draw a line segment AB = 3.2 cm.
(ii) Draw rays at A and B making angle of 120° each and cut off AF = BC = 3.2 cm.
(iii) Similarly at F and C, draw rays making angle of 120° each and cut off FE = CD = 3.2 cm.
(iv) Join ED.
ABCDEF is a regular hexagon.
(v) Draw the angle bisector of ∠A and ∠B which intersect each other at O.
(vi) From O, draw OL ⊥ AB.
(vii) With centre O and radius OL draw a circle which will touch the sides of regular hexagon ABCDEF.
This is the required incircle of the hexagon.

Que-16: Draw a regular hexagon of side 2.8 cm and circumscribe a circle on it.
Sol: Steps of construction :
(i) Draw a line segment AB = 2.8 cm.
(ii) At A and B draw rays making angle of 120° each and cut off AF = BC = 2.8 cm.
(iii) Similarly at F and C, draw rays making angle of 120° and cut off FE = CD = 2.8 cm.
(iv) Join ED.
ABCDEF is a regular hexagon.
(v) Draw the perpendicular bisector of AB and AF which intersect each other at O.
(vi) With centre O and radius OA, draw a circle which passes through the vertices of hexagon ABCDEF. This is the required circumcircle of regular hexagon.

–: End of Circles Class 10 OP Malhotra Exe-14F ICSE Maths Solutions / Answer of Ch-14 :–
Return to :- OP Malhotra S Chand Solutions for ICSE Class-10 Maths
Thanks
Please Share with Your Friends