Combination of Capacitors Numerical for Class-12 Nootan ISC Physics Ch-4 Capacitors and Dielectrics. Step by step solutions of Kumar and Mittal Physics of Nageen Prakashan as council latest prescribe guideline for upcoming exam. Visit official Website CISCE for detail information about ISC Board Class-12 Physics.

Combination of Capacitors Numerical for Class-12 Nootan ISC Physics Ch-4 Capacitors and Dielectrics
| Board | ISC |
| Class | 12 |
| Subject | Physics |
| Book | Nootan |
| Chapter-4 | Capacitors and dielectrics |
| Topics | Numericals on Combination of Capacitors |
| Academic Session | 2025-2026 |
Numericals on Combination of Capacitors
Combination of Capacitors Numerical for Class-12 Nootan ISC Physics Ch-4 Capacitors and Dielectrics
Que-20. Three equal 9 pF capacitors are connected in series. Find (a) the total capacitance of the combination, (b) PD across each capacitor if the combination is connected to a 120 V supply.
Ans-20 (a) in case of n equal capacitor in series net capacitance
=> C/n
=> 9 pF/3 = 3 pF
(b) voltage across each capacitor
=> V/n
=> 120/3 = 40 V
Que-21. Three capacitors of 2 PF, 3 pF and 4 pF capacitances are connected in parallel. Find (a) the total capacitance of the combination, (b) charge on each capacitor if the combination is connected to a 100 V supply.
Ans-21 (a) in case of parallel combination capacitance of capacitor are added i.e.
net capacitance = 2+3+4 = 9 pF
(b) charge on capacitor
Q = CV
Charge on 2 pF capacitor = 2 x 10^-12 x 10
=> 2 x 10^-10 C
Charge on 3 pF capacitor = 3 x 10^-12 x 10
=> 3 x 10^-10 C
Charge on 4 pF capacitor = 4 x 10^-10 C
Que-22. Two capacitors have an equivalent capacitance of 24 µF when joined in parallel and of 6 µF when joined in series. What are their individual capacitances?
Ans-22 Let the capacitor are C1 , C2
C1 + C2 = 24
C1C2/C1+C2 = 6 {net capacitance of two capacitors in series = C1C2/C1+C2}
=> C1C2 /24 = 6 => C1C2 = 144
=> (C1-C2)^2 = (C1+C2)^2 – 4 C1C2
=> 24^2 – 4 X 144 = 0
=> C1 = C2 = 24/2 = 12 µF
Que-23. How and how many capacitors each having capacitance of 2.0 µF should be connected so that the total potential difference of the arrangement becomes 300 V, if the arrangement is given a charge of 75 µC.
Ans-23 C = Q/V = 75 x 10^-6 / 300 = 1/4 µF
Since net capacitance is less than each capacitor (2 µF) therefore capacitors should be added in series
Let n capacitor are added
then 2/n = 1/4
=> n = 8
Que-24. We have two variable capacitors; each of them can be varied from 10 pF to 500 pF. What minimum and maximum capacitances can be obtained by combining them?
Ans-24 minimum values can be obtained by adding in series of least value i.e. 10/2 = 5 µF
again maximum value can be obtained by adding maximum value in parallel i.e. 500 + 500 = 1000 µF
Que-25. Three equal capacitors joined in parallel take a total charge of 1.8 µC from a 2 V cell. How much charge will they take from the same cell, if joined in series?
Ans-25 net capacitance in parallel
= Cparallel = Q/V = 1.8/2 = 0.9
again Cparallel/Cseries = n^2 {n = no. of capacitor}
=> 0.9/Cseries = (3)^2
=> Cseries = 0.9/9 = 0.1 µF
Therefore Charge in series = Q = CV
=> Q = 0.1 x 2 = 0.2 µF
Que-26. Two parallel-plate capacitors, 20 µF and 30 µF are charged to 30 V and 20 V respectively. If their plates with same type of charges are connected together, then find the common PD between the plates of the capacitors.
Ans-26 common potential of two capacitors
V = C1V1 + C2V2 / C1 + C2
=> 20 x 30 + 30 x 20 / 20 + 30
=> 1200/50 = 24 volt
Que-27. A 0.2 µF capacitor is charged to a potential of 600 V. After disconnecting the battery, it is connected in parallel to a 1.0 µF capacitor. What will be the new potential?
Ans-27 C1 = 0.2 µF V1 = 600 V
C2 = 1.0 µF V2 = 0
common potential
V = C1V1 + C2V2 / C1 + C2
=> 0.2 x 600 + 0 / 1.2
=> 1200/12 = 100 V
Que-28. A 80 µF capacitor is charged by a 50 V battery. The capacitor is disconnected from the battery and then connected across another uncharged 320 µF capacitor. Find the charge on the second capacitor.
Ans-28 Common potential
V = 80 x 50 + 320 x 0 / 320 + 80
=> 4000 / 400 = 10V
Charge on second capacitor
Q = CV
=> 320 x 10 = 3200 µC
Que-29. Two capacitors 4 µF and 2 µF are connected in parallel with a battery of 6 V. Find (i) PD across each capacitor, (ii) charge on each.
Ans-29 PD in case of parallel combination remains same through each capacitor
(i) Therefore, PD across each capacitor = 6 V
(ii) charge = CV
Therefore on 4µF = 4 x 6 = 24 µC
on 2 µF = 2 x 6 = 12 µC
Que-30. There are three capacitors each of 0.50 µF. Two of these are connected in series and the third is connected in parallel to them. Calculate the capacitance of the combination. If a potential difference of 20 V is applied on the combination, what will be the total charge stored?
Ans-30 Total capacitance
=> 0.5/2 + 0.5 = 0.75 µF
Total charge Q = CV
=> 20 x 0.75 = 15 µC
Que-31. Four capacitors of 2, 6, 12 and 20 µF are joined in parallel. Determine the equivalent capacitance. If this arrangement is charged at a potential of 1000 V, then determine the quantity of charge on it. What will be the charge on the 12 µF capacitor? Energy in 20 µF capacitor?
Ans-31 net capacitance in parallel = 2 + 6 + 12 + 20 = 40 µF
Total charge = CV = 40 x 1000 = 40000 µC {Voltage in parallel remains same}
charge on 12 µF capacitor
=> Q = CV = 12 x 1000 = 12000 µC
energy of 20 µF capacitor = 1/2 CV^2 = 1/2 x 20 x (1000)^2 x 10^-6
=> 10 J
Que-32. A potential difference of 120 V is applied to combination of two capacitors C₁ = 4 µF and C2 = 12 µF connected in series. Calculate (a) the effective capacitance of the combination and (b) the potential difference and charge for each of these two capacitors.
Ans-32 (a) Effective capacitance of two capacitor in series
C = C1C2/C1+C2 = 4 x 12 / 16 = 3 µF
(b) Charge on each capacitor
=> Q = CV = 3 x 120 = 360 µC
and potential difference
on 4 µF capacitor = 360/4 = 90 V
on 12 µF capacitor = 360/12 = 30 V
Note: in case of series combination charge on each capacitor and system is same.
Que-33. Two capacitors of 3.0 µF and 6.0 µF are connected in series, and a potential difference of 120 V is applied to this combination. What is the potential difference between the plates of the 3.0 µF capacitor? What is the energy in the 6.0 µF capacitor?
Ans-33 Net Capacitance of capacitor
C = C1C2/C1+C2 = 3 x 6 / 9= 2 µF
charge on system and each capacitor
Q = CV = 2 x 120 = 240 µC
again PD across 3 µF capacitor
=> 240/3 = 80 volt
energy of 60 µF capacitor
U = 1/2 Q^2/C = 1/2 x 240 x 240 x 10^-12/6 x 10^-6
=> 4.8 x 10^-3 J
Note: Since in series combination charge is same therefore apply formula 1/2 Q^2/C in place of 1/2 CV^2
Que-34. Two capacitors are 2 and 3 µF and are joined in series. The outer plate of the first capacitor is at 1000 V and the outer plate of the second capacitor is earthed. Find out the potential and charge of the inner plate of each capacitor.
Ans-34 Net capacitance = 2×3/5 = 1.2 µF
Therefore charge on combination as well as in each capacitor
Q = CV = 1.2 x 10^-6 x 1000 = 1.2 x 10^-3
again potential on 2 µF capacitor = 1.2 x 10^-3 / 2 x 10^-6 = 600 V
and 3 µF capacitor = 1.2 x 10^3 / 3 x 10^-6 = 400 V
Net capacitance in series combination = 2 x 3 / 2 + 3 = 1.2 µF
Total charge = Q = CV = 1.2 x 1000 = 1200 µC = 1.2 x 10^-3 C
Therefore potential on 2 µF capacitor = 1200 / 2 = 600 V
potential on 3 µF capacitor = 1200 / 3 = 400 V
Net charge in series combination = charge in each capacitor therefore charge on each capacitor = 1.2 x 10^-3 C
Que-35. A 600 pF capacitor is charged by a 200 V supply. It is then disconnected from the supply and is connected in parallel to another uncharged 600 pF capacitor. How much electrostatic energy is lost in this process? Where does this energy go?
Ans-35 Initial energy
U1 = 1/2 CV^2 = 1/2 x 600 x 10^-12 x (200)^2
=> 12 x 10^-6 J = 1.2 x 10^5 J
common potential
V = C1V1 + C2V2 / C1 + C2
=> 600 x 200 + 600 x 0 / 1200
=> 100 V
final capacitance = 600 + 600 = 1200 pF
Therefore final energy = U2 = 1/2 x 1200 x 10^-12 x (100)^2
=> 6 x 10^-6 J
Therefore ΔU = 12 x 10^-6 – 6 x 10^-6
=> 6 x 10^-6 J
Que-36. A 100 pF capacitor is charged to a potential difference of 100 V. It is connected in parallel to another capacitor. If the final voltage be 30 V, then what will be the capacitance of the second capacitor? How much energy will be wasted and what will happen to it?
Ans-36 Let another capacitor has capacitance C then
30 = 100 x 100 + 0 / 100 + C
=> 100 + C = 1000/3
=> C = 700/3 pF = 7/3 x 10^-10 F
again loss of energy ΔU = 1/2 x 100 x 10^-12 x 100^2 – 1/2 x 1000/3 x 10^-12 x 30^2
=> 3.5 x 10^-7 J
it will appear as heat
Que-37. An electronic flash lamp has 20 capacitors, each of capacitance 5 µF, connected in parallel. The lamp is operated at 100 V. How much energy will be radiated in a flash?
Ans-37 Net capacitance = 20 x 5 µF = 100 X 10^-6F
V = 100 V
energy = 1/2 CV^2 = 1/2 x 100 x 10^-6 x 100^2
=> 0.5 J
Que-38. Three capacitors capacitance C₁ = 3 µF, C2 = 6 µF and C3 = 10 µF, are connected to a 10V battery as shown in figure. Calculate: (a) equivalent capacitance. (b) electrostatic potential energy stored in the system.
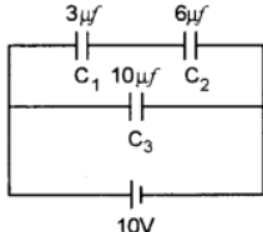
Ans-38 the equivalent capacitance of the series combination of C1 and C2 is
C12 = C1C2/C1+C2
=> 3 x 6 / 3 + 6 = 2 µF
this is in parallel with C3
(a) So the equivalent capacitance of the combination of all three capacitors is
Ceq = C12 + C3
=> 2 x 10 = 12 µF
(b) Electrostatic PE stored in the system is
E = 1/2 Ceq V^2
=> 1/2 x 12 x 10^2
=> 600 µJ = 6 x 10^-4 J
Que-39. In the given combination of capacitors, the PD between the points A and B is 40 V. Find the effective capacitance between these points and charge on each capacitor.
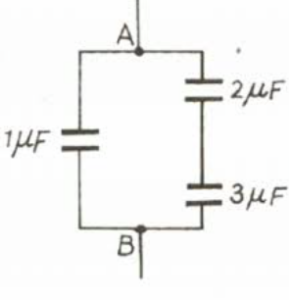
Ans-39 2 µF and 3 µF are in series with 1 µF in parallel
Net capacitance = 2×3/2+3 + 1 = 2.2 µF
Therefore charge on combination
=> 2.2 x 40 = 88 µC
again charge on 1 µF
=> Q = CV = 1 x 40 = 40 µC
and charge on 2 µF and 3 µF
=> 88 µC – 40 µC = 48 µC
Que-40. Calculate the capacitance C in the given figure. The equivalent capacitance of the combination between P and Q is 30 μΕ.

Ans-40 20 µF 20 µF 0 µF are in parallel
Therefore net capacitance = 20 x 3 = 60 µF
again C is in series
Therefore net capacitance = 60xC/60+C = 30
=> C = 60 µF
Que-41. Calculate the equivalent capacitance between the points A and B in the given combination.
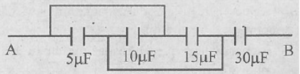
Ans-41 Net capacitance = (5 + 10 + 15) x 30 / 5 + 10 + 15 + 30
=> 30 x 30 / 60 = 15 µF
Que-42. In the given network, calculate (i) equivalent capacitance between A and B, (ii) if a voltage of 150 V is applied between A and B calculate the PD between the plates of 6 µF capacitance.
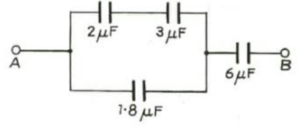
Ans-42 net capacitance of rectangle = 2×3/2+3 + 1.8 = 3 µF
now net combination of capacitance = 3×6/3+6 = 2µF
V1:V2 = 1/C1:1/C2
=> V1:V2 = 1/3 : 1/6 = 2:1
Therefore V2 = 1/3 x 150 = 50 V
— : End of Combination of Capacitors Numerical for Class-12 Nootan ISC Physics Ch-4 Capacitors and Dielectrics. :–
Return to : – Nootan Solutions for ISC Class-12 Physics
Thanks
Please share with your friends