Complex Numbers Class 11 OP Malhotra Exe-9C ISC Maths Solutions Ch-9 Solutions. In this article you would learn about Modulus or Absolute value of Complex Number. Step by step solutions of latest textbook has been given as latest syllabus. Visit official Website CISCE for detail information about ISC Board Class-11 Mathematics.

Complex Numbers Class 11 OP Malhotra Exe-9C ISC Maths Solutions Ch-9
| Board | ISC |
| Publications | S Chand |
| Subject | Maths |
| Class | 11th |
| Chapter-9 | Complex Numbers |
| Writer | O.P. Malhotra |
| Exe-9(C) | Modulus or Absolute value of Complex Number. |
Exercise- 9C
Complex Number Class 11 OP Malhotra Exe-9C Solution.
Que-1: If (- 2 + √-3) (- 3 + 2√-3) = a + bi, find the real numbers a and b with values of a and b, also find the modulus of a + bi.
Sol: (- 2 + √-3) (- 3 + 2√-3) = a + bi
⇒ (- 2 + √-3i)(- 3 + 2√-3i) = a + ib
⇒ 6 – 4√-3i – 3√-3i – 6 = a + ib
⇒ – 7√-3i = a + ib
On comparing real and imaginary parts on both sides, we get
a = 0 ; b = – 7√-3
∴ |a + ib | = |0 + (- 7√-3)i| = 7√-3
Que-2: Find the modulus of (1 – i)-2 + (1 + i)-2.
Sol: (1 – i)¯² + (1 + i)¯² = 1/(1−i)² + 1/(1+i)²
= 1/(1−1−2i) + 1/(1−1+2i)
= (−1/2i) + (1/2i) = 0
∴ |1(1 – i)-2 + (1 + i)-2| = |0| = 0
Que-3: If z = 6 + 8i, verify that
(i) | z | = | z¯ |
(ii) – | z | < Re (z) ≤ | z |
(iii) – | z | < Im (z) ≤ | z |
(iv) z-1 = z¯ / |z|²
Sol: Given z = 6 + 8i ∴ z¯ = (6+8i)¯ = 6 – 8i
(i) | z | = 6 + 8i = √(6²+8²)
= √(36+64) = √100 = 10
|z| = |6 – 8i| = √(6²+(-8)²)
= √(36+64) = √100 = 10
∴ |z| = |z¯|
(ii) since – 10 ≤ 8 ≤ 10
⇒ – | z | ≤ Re (z) ≤ | z |
(iii) since – 10 ≤ 8 ≤ 10
⇒ – | z | ≤ Im (z) ≤ | z |
(iv) z‾¹ = (6 + 8i)‾¹ = {1/(6+8i)} × {(6−8i)/(6−8i)}
= (6−8i)/(36+64) = (6−8i)/100
and z¯ / |z|² = (6−8i)/[√(6²+8²)]² = (6−8i)/100
∴ z‾¹ = z¯ / |z|²
Que-4: If z1 = 3 + 4i, z2 = 8 – 15i, verify that
(i) | – z1| = | z1|
(ii) | z²1| = |z1|²
(iii) |z1z2| = |z1| |z2|
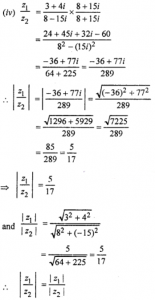
(iv) ∣∣z1 / z2∣∣=|z1| / |z2|
(v) | z1| + z2| < | z1| + | z2 |
(vi) | z2 – z1 | > ||z2|−|z1||
(vii) |z1 + z2|² + |z1 – z2|² = 2(|z1|² + | z2|²).
Sol: z1 = 3 + 4i; z2 = 8 – 15i
(i) – z1 = – (3 + 4i) = – 3 – 4i
∴ |- z1 | = √{(-3)²+(-4)²} = √(9+16) = 5
| z, | = √(3²+4²) = √(9+16) = √25 = 5
∴ |- z1 | = | z1|
(ii) z1² = (3 + 4i)² = 9 – 16 + 24i
= – 7 + 24i
∴ ∣∣z21∣∣ = √((-7)²+24²)
= √(49+576) = √625 = 25
|z1|² = (√3²+4²)²
= 9 + 16 = 25
∴ ∣∣z21∣∣ = |z1|²
(iii) z1z2 = (3 + 4i) (8 – 15i)
= 24 – 45i + 32i + 60
⇒ z1z2 = 84 – 13i
∴ |z1z2| = √(84²+(-13)²)
= √(7056+169) = √7225 = 85
Here, | z1 | | z2 | = | 3 + 4i | | 8 – 15i |
= √(3²+4²) √(8²+(-15²))
= √(9+16) √(64+225)
= √25 √289 = 5 x 17 = 85
∴ |z1z2| = |z1| |z2|
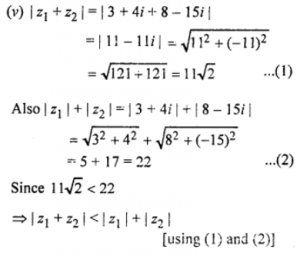
(vi) |z2 – z1 | = | 8 – 15i – 3 – 4i | = | 5 – 19i |
= √(5²+(-19)²) = √(25+361)
= √386 … (1)
||z2| − |z1|| = ∣∣√(8²+(-15²)) − √(3²+4²)∣∣
= | 17 – 5 | = 12
From (1) and (2); we have
|z2−z1| > ||z2| − |z1|| [∵ √386 > 12]
(vii) z1 + z2 = 3 + 4i + 8 – 15i = 11 – 11i
and z1 – z2 = 3 + 4i – 8 + 15i = – 5 + 19i
L.H.S = | z1 + z2|² + | z1 – z2|
= | 11 – 11i |² + | – 5 + 19i |²
= (√(11²+(-11)²))² + (√(-5)²+19²)²
= (√(121+121))² + (√(25+361))²
= (11√2)² + (√386)²
= 242 + 386 = 628
R.H.S = 2(|z1|²+|z2|²)
= 2 ((√(3²+4²))² + (√(8²+(-15)²))²)
= 2 (25 + 289) = 2 x314 = 628
∴ L.H.S = R.H.S.
Que-5: Find the modulus of the following using the property of modulus.
(i) (3 + 4i) (8 – 6i)
(ii) (8+15i)/(8−6i)
(iii) (3+2i)/(2−5i) + (3−2i)/(2+5i)
(iv) {(2−3i)(4+5i)} / {(1−4i)(2−i)}
Sol: (i) Let z = (3 + 4i) (8 – 6i)
∴ | z | = |(3 + 4i)(8 – 6i)|
= | 3 + 4i | | 8 – 6i | [∵ |z1z2 | = | z1 | | z2 |]
= √(3²+4²) √(8²+(-6)²)
= √(9+16) √(64+36) = 5 x 10 = 50
(ii) Let z = (8+15i)/(8−6i)
|z| = |8+15i| / |8-6i|
= √(64+225) / √(64+36)
= 17/10
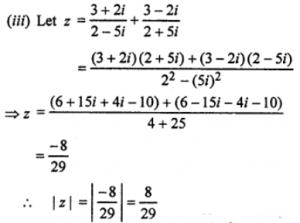
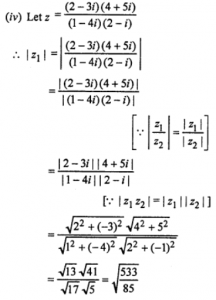
Que-6: Let z be a complex number such that ∣∣(z−5i)/(z+5i)∣∣ = 1, then show that z is purely real.
Sol: Let z = x + iy
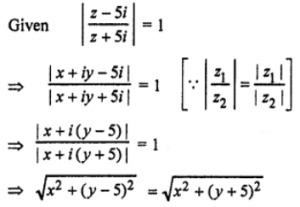
On squaring both sides, we have
x² + (y – 5)² = x² + (y + 5)²
⇒ x² + y² + 25 – 10y = x² + y² + 25 + 10y
⇒ 20y = 0
⇒ y = 0
∴ z = x, which is purely real.
Que-7: If z is a complex number such that
| z – 1 | = | z + 1|, show that Re (z) = 0.
Sol: Given |z – 1 | = |z + 1|; where z = x + iy
⇒ |x + iy – 1 | = |x + iy + 1|
⇒ |(x – 1) + zy | = |(x + 1) + iy |
⇒ (√{(x-1)²+y²} = √{(x+1)²+y²}
On squaring both sides ; we have
(x – 1)² + y² = (x + 1)² + y²
⇒ x² – 2x + 1 = x² + 2x + 1
⇒ 4x = 0
⇒ x = 0
⇒ Re (z) = 0
Que-8 Solve: | z | + z = 2 + i, where z is a complex number.
Sol: Given | z | + z = 2 + i; where z = x + iy
⇒ √(x²+y²) + x + iy = 2 + i
Comparing real and imaginary parts on both sides ; we have
√(x²+y²) + x = 2 …(1)
and y = 1 … (2)
∴ from (1) and (2); we have
√(x²+1) = 2 – x ;
on squaring both sides, we have
⇒ x² + 1 = (2 – x)²
⇒ x² + 1 = 4 + x² – 4x
⇒ 3 – 4x = 0 ⇒ x = 3/4
∴ required complex number z = 3/4 + 1
Que-9: If |z1| = (z1 ≠ 1) and z2 = (z1-1)/(z1+1), then show that real part of z2 is zero.
Sol: Let z1 = x + yi
|z1| = √(x²+y²) = 1 ……[Given that |z1| = 1]
⇒ x2 + y2 = 1 ……(i)
Now z2 = (z1-1)/(z1+1)
= (x+yi-1)/(x+yi+1)
= {(x+1)+yi}/{(x+1)+yi}
= [{(x-1)+yi}/{(x+1)+yi}] × {(x+1-yi)/(x+1-yi)}
= {(x-1)(x+1)-y(x-1)i+y(x+1)i-y²i²} / {(x+1)²-y²i²}
= {x²-1+yi(x+1-x+1)+y²}/{x²+1+2x+y²}
= {(x²+y²-1)+2yi}/{x²+y²+2x+1}
= [(1-1)/{x²+y²+2x+1}] + [2y/{x²+y²+2x+1i}]i
= 0 + [2y/(x²+y²+2x+1)]i
Hence, the real part of z2 is 0.
Que-10: If (z-1)/(z+1) is a purely imaginary number (z-1), then find the value of |z|.
Sol: Let z = x + iy
Then,
(z−1)/(z+1) = (x+iy−1)/(x+iy+1)
= {(x−1)+iy}/{(x+1)+iy} × {(x+1)−iy}/{(x+1)−iy}
= {x²+x−ixy−x−1+iy+ixy+iy−i²y²} / {(x+1)²−i²y²}
= {x²+y²−1+2iy} / {x²+1+2x+y²} [∵i² = −1]
If (z−1)/)z+1) is purely imaginary number, then
Re {(z−1)/(z+1)} = 0
⇒ x²+y²−1 = 0
⇒ x² + y² = 1
⇒ |z|² = 1
⇒ |z| = 1
Thus, the value of |z| is 1.
Que-11: If z1 = 2-i, z2 = 1+i, find |(z1+z2+1)/(z1-z2-1)|
Sol: z1 = 2-i, z2 = 1+i
∴ |(z1+z2+1)/(z1-z2+1)| = |{(2-i)+(1+i)+1}/{(2-i)-(1+i)+1}|
= |4/(2-2i)| = |4/{2(1-i)}|
= |{2/(1-i)} × {(1+i)/(1+i)}| = |{2(1+i)}/(1²-i²)|
= |{2(1+i)}/(1+1)| [i2 = – 1]
= |{2(1+i)}/2|
= 1+i = √(1² +1²) = √2
The value of this type is |(z1+z2+1)/(z1-z2+1)| = √2
–: End of Complex Number Class 11 OP Malhotra Exe-9C ISC Math Ch-9 Solution :–
Return to :- OP Malhotra ISC Class-11 S Chand Publication Maths Solutions
Thanks
Please share with your friends


