Complex Numbers Class 11 OP Malhotra Exe-9D ISC Maths Solutions Ch-9. In this article you would learn about Trigonometric and Argument of a Complex Number. Step by step solutions of latest textbook has been given as latest syllabus. Visit official Website CISCE for detail information about ISC Board Class-11 Mathematics.

Complex Numbers Class 11 OP Malhotra Exe-9D ISC Maths Solutions Ch-9
| Board | ISC |
| Publications | S Chand |
| Subject | Maths |
| Class | 11th |
| Chapter-9 | Complex Numbers |
| Writer | O.P. Malhotra |
| Exe-9(D) | Trigonometric and Argument of a Complex Number. |
Exercise- 9D
Complex Number Class 11 OP Malhotra Exe-9D Solution.
Find the modulus and amplitude of the following complex numbers and hence express them into polar form.
Que-1: √3 + i
Sol: Let z = √3 + i = x + iy
Here x = √3 > 0 and y = 1 > 0
∴ point (x, y) i.e. (-√3, 1)
lies in first quadrant.
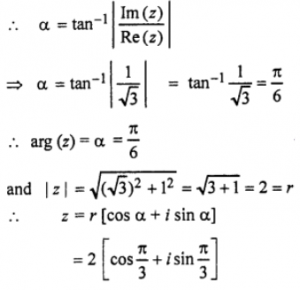
Que-2: -√3 + 1
Sol: Let z = – √3 + i …(1)
put – √3 = r cos θ …(2)
1 = r sin θ …(3)
On squaring and adding (1) and (2);
3 + 1 = r² (cos² θ + sin² θ)
⇒ r² = 4
⇒ r = 2 (r > 0)
On dividing (3) by (2); we have tan θ
tan θ = – 1/√3 = – tan π/6 = tan (π – (π/6))
[∵ cos θ < 0 and sin θ > 0
∴ θ lies in 2nd quad]
⇒ θ = 5π/6
⇒ arg (z) = 5π/6
∴ from eqn. (1) ; we have
z = r [cos θ + i sin θ]
= 2 [cos 5π/6 + i sin 5π/6 ]
Que-3: -2 + 2√3i
Sol: Let z = – 2 + 2√3 i … (1)
put – 2 = r cos θ …(2)
2√3 = r sin θ …(3)
since cos θ < 0 and sin θ > 0 ∴ θ lies in 2nd quadrant.
On squaring and adding (2) and (3); we have
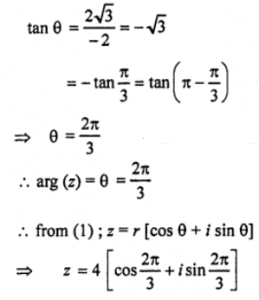
which is the required polar form.
Que-4: -1 – i
Sol: Let z = – 1 – i = x + iy
Here x = – 1 < 0 and y = – 1 < 0
∴ point (x, y) i.e. (- 1, – 1) lies in IIIrd quadrant.
∴ tan θ = ∣∣(Im(z)) / (Re(z))∣∣ = ∣∣ y/x ∣∣ = ∣∣ −1/−1 ∣∣ = 1
⇒ α = π/4
∴ arg (z) = – (π – α) = – (π – (π/4)) = – 3π/4
and r = √(x²+y²) = √{(-1)²+(-1)²} = √2
Thus required polar form of z is given by
z = r [cos (arg z) + z sin (arg z)]
⇒ z = √2[cos(−3π/4) + i sin(−3π/4)]
Que-5: -2i
Sol: Let z = – 2i × x + iy
∴ |z| = |- 2i| = 2
where x – 0 ; y = – 2
∴ point (x, y) i.e. (0, – 2) lies in IVth quadrant.
∴ tan θ = ∣∣ (Im(z)) / (Re(z)) ∣∣ = ∣∣−2/0∣∣ → ∞ ⇒ α = π/2
∴ θ = arg (z) = – α = – π/2
Thus polar form of z is given by z = | z | (cos θ + z sin θ)
= 2 [cos(−π/2) + i sin(−π/2)]
Que-6: -1 – √3i
Sol: Let z = – 1 – √3 i …(1)
put – 1 = r cos θ …(2)
– √3 = r sin θ …(3)
Here cos θ, sin θ < 0
∴ θ lies in 3rd quadrant. On squaring and adding eqn. (2) and eqn. (3); we have
r² (cos² θ + sin² θ) = (- 1)² + (- √3)² = 1 + 3 = 4
r² = 4 ⇒ r = 2 (∵ r > 0)
On dividing eqn. (3) by eqn. (2); we have
tan θ = (−√3/1) = √3
= tan (π/3) = tan[−(π−(π/3))]
⇒ θ = – 2π/3
∴ from (1) ; z = r [cos θ + i sin θ]
i.e. z = 2[cos(−2π/3) + i sin(−2π/3)]
Que-7: -2
Sol: Let z = – 2 = x + iy
Here x = – 2 and y = 0
∴ (- 2, 0) lies on negative x-axis.
∴ | z | = | – 2 | = 2
∴ arg (z) = π ;
∴ z = 2 [cos π + i sin π] be the required polar form.
Que-8: {(1+i)^13} / {(1−i)^7}
Sol: Let
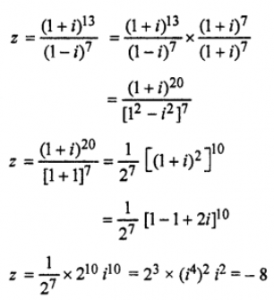
|z| = |-8| = 8
Further x = – 8 ; y = 0 i.e. point (- 8, 0) lies on negative real axis.
∴ arg (z) = π
∴ z = 8 [cos π + i sin π] be the required polar form
Que-9: (3+i) (4+i)
Sol: Let z = (3+ i) (4 + i)
= 12 + 3i + 4i – 1 = 11 + 7i …(1)
∴ | z | = √(11²+7²)
= √(121+49) = √170
put 11 = r cos θ …(2)
7 = r sin θ …(3)
On dividing (3) by (2); we have
tan θ = 7/11
⇒ θ = tan¯¹ (7/11) = tan¯¹ (0.636)
⇒ θ = 32°29′
[since cos θ, sin θ > 0
∴ θ lies in first quadrant]
∴ arg (z) = θ = 32° 29′
∴ from (1); z = r [cos θ + i sin θ]
⇒ z = √170 [cos (32° 29′) + i sin (32° 29′)]
[On squaring and adding eqn. (1) and (2); r = √170 ]
Que-10: {(1+i)(2+i)} / (3+i)
Sol: Let z = {(1+i)(2+i)/(3+i) = (2+i+2i−1)/(3+i) = (1+3i)/(3+i) × (3−i)/(3−i)
⇒ z = (3−i+9i+3)/(3²−i²)
⇒ z = (6+8i)/(9+1) = (3+4i)/5 = (3/5) + (4/5)i … (1)
∴ | z | = {√(3²+4²)/5} = 5/5 = 1
Put 3/5 = r cos θ … (2)
and 4/5 = r sin θ … (2)
On squaring and adding eqn. (2) and (3);
(3/5)² = r² (cos² θ + sin² θ)
⇒ r² = {(9+16)/25} 1 (∵ r > 0)
On dividing eqn. (3) by eqn. (2); we have
tan θ = (4/5) × (5/3) = 4/3 = 1.3333
⇒ θ = tan¯¹ (1.3333) = 53° 8′ [∵ θ lies in first quadrant]
∴ from (1); z = r [cos θ + i sin θ]
⇒ z = 1 [cos (53° 8′) + i sin (53° 8′)]
which is the required polar form.
Que-11: (5-i)/(2-3i)
Sol: Let z = {(5-i)/(2-3i)} × {(2+3i)/(2+3i)}
= (10+15i-2i+3)/(2²-(3i)²)
= (13+13i)/(4+9)
= 1 + i
|z| = |1+i| = √(1²+1²) = √2
Let z = 1 + i = x + iy
Here, x = y = 1 > 0
point (x,y) i.e., (1,1)
lies in first quadrant
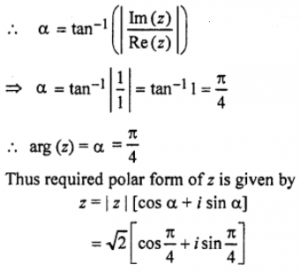
Que-12: {(3+4i)(4+5i)} / {(4+3i)(6+7i)}
Sol: Let z = {(3+4i)(4+5i)} / {(4+3i)(6+7i)}

= 0.3288
⇒ α = 18° 12′ and arg (z) = a = 18° 12′
∴ required polar form of z be given by z = | z | [cos α + i sin α]
⇒ z = √(41/85) [cos (18° 12′)+ i sin (18° 12′)]
Que-13: Change the following complex numbers into polar form.
(i) – 4 + 4√3 i
(ii) (1+3i)/(1−2i)
(iii) (1+2i)/{1−(1−i)²}
(iv) {(3+4i)(4+5i)} / {(4+3i)(6+7i)}
Sol: (i) Let z = – 4 + 4√3i …(1)
put – 4 = r cos θ …(2)
4√3 = r sin θ …(3)
On squaring and adding eqn. (2) and eqn. (3); we have
r² = (- 4)² + (4√3)² = 16 + 48 = 64
⇒ r = 8 (∵ r > 0)
since cos θ < 0 and sin θ > 0 ∴ θ lies in 2nd quadrant.
On dividing eqn. (3) by eqn. (2); we have
tan θ = – √3 = – tan (π/3) = tan(π – (π/3))
= tan (2π/3)
∴ θ = (2π/3)
∴ from (1); z = r [cos θ + i sin θ]
⇒ z = 8[cos (2π/3) + i sin (2π/3)]
which is the required polar form
(ii) Let z = (1+3i)/(1−2i) × (1+2i)/(1+2i)
⇒ z = {1+2i+3i−6}/(1²−(2i)²) = (5i−5)/(1+4) = i – 1
⇒ z = – 1 + i …(1)
put – 1 = r cos θ …(2)
and 1 = r sin θ …(3)
since cos θ < 0 and sin θ > 0
∴ θ lies in 2nd quadrant.
On squaring and adding eqn. (1) and (2); we have
r² (cos² θ + sin² θ) = (- 1)² + (1)²
⇒ r² = 2 ⇒ r = √2 (∵ r > 0)
On dividing eqn. (3) by eqn. (2); we have
tan θ = – 1 = – tan (π/4) = tan (π – (π/4))
⇒ θ = π – (π/4) = 3π/4
∴ from (1); z = r [cos θ + 2 sin θ]
⇒ z = √2[cos (3π/4) + i sin (3π/4)]
which is the required polar form.
(iii) Let z = (1+2i)/{1−(1−i)²} = (1+2i)/{1−(1−1−2i)}
⇒ z = (1+2i)/(1+2i) = x + iy
Here x = 1 ; y = 0
∴ point (x, y) i.e. (1,0)
lies on positive real axes.
∴ z = 1 = 1 + i0 = cos 0° + 2 sin 0°
which is the required polar form.
(iv) Let z = (1+7i)/{(2−i)²} = (1+7i)/(4−1−4i) = (1+7i)/(3−4i) × (3+4i)/(3+4i)
⇒ z = (3+4i+21i−28)/(3²−(4i)²) = (−25+25i)/(9+16)
⇒ z = – 1 + i … (1)
put – 1 = r cos θ …(2)
and 1 = r sin θ … (3)
since cos θ < 0 and sin θ > 0 ∴ lies in 2nd quadrant.
On squaring and adding eqn. (1) and (2); we have
r² (cos² θ + sin² θ) = (- l)² + (l)²
⇒ r² = 2 ⇒ r = √2 (∵ r > 0)
On dividing eqn. (3) by eqn. (2); we have
tan θ = – 1 = – tan tan (π/4) = tan (π−(π/4))
⇒ θ = π – (π/4) = π/4
∴ from (1) ; z = r [cos θ + i sin θ]
⇒ z = √2[cos(3π/4) + i sin(3π/4)]
which is the required polar form.
Que-14: Given the complex number z = (−1+√3i)/2 and w = (−1−√3i) / 2 (where i = √-1)
(i) Prove that each of these complex numbers is the square of the other.
(ii) Calculate the modulus and argument of w and z.
(iii) Calculate the modulus and argument of wz.
(iv) Represent z and w accurately on the complex plane.
Sol: Given : z = (−1+√3i)/2 and w = (−1−√3i)/2
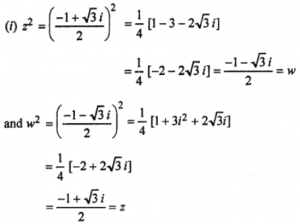
Thus each of the complex numbers is the square of the other.
(ii) z = – (1/2) + (√3/2) = x + iy
Here, x = -1/2 < 0 and y = √3/2 > 0
Then the point (x,y) i.e., [(1/2), (√3/2)] lies in 2nd quadrant
|z| = √{(1/2)²+(√3/2)²}
= √{(1/4)+(3/4)} = 1
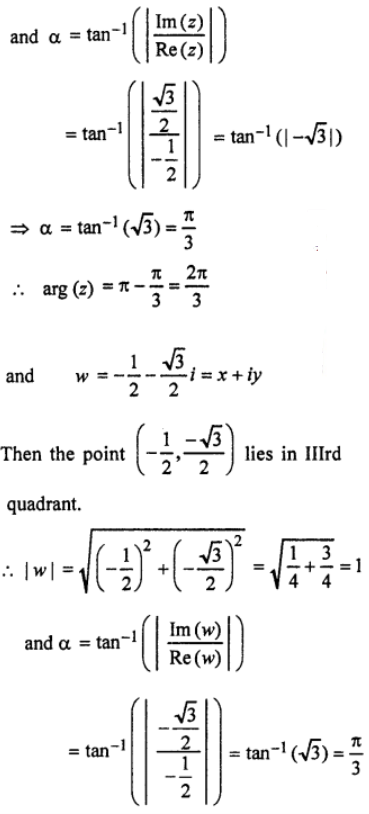
arg (z) = – (π-a) = – {π-(π/3)} = -2π/3
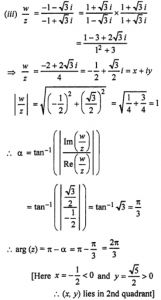
(iv) Clearly the complex number z is represented by point P {(−1−√3i)/2} and the complex number is represented by point Q {(−1−√3i)/2} in complex plane.
Que-15: If arg (z-i) = arg (z+3i), then find (x-1) : y when z = x+iy
Sol: Given that: arg(z – 1) = arg(z + 3i)
⇒ arg[x + yi – 1] = arg[x + yi + 3i]
⇒ arg[(x – 1) + yi] = arg[x + (y + 3)i]
⇒ tan¯¹ {y/(x-1)} = tan¯¹ {(y+3)/x}
⇒ {y/(x-1)} = {(y+3)/x}
⇒ xy = (x – 1)(y + 3)
⇒ xy = xy + 3x – y – 3
⇒ 3x – y = 3
⇒ 3x – 3 = y
⇒ 3(x – 1) = y
⇒ {(x-1)/y} = 1/3
⇒ x – 1 : y = 1 : 3
Hence, x – 1 : y = 1 : 3.
Que-16: Let z = x+iy be a complex number such that arg {(z-1)/(z+1)} = π/2, then show that x²+y² = 1
Sol: Given, z = x + iy and
arg ((z+1)/(z−1)) = π/2 …(i)
∴ (z+1)/(z−1) = {(x+iy+1)/(x+iy−1)} × [{(x+1)−iy]/{(x+1)−iy}]
= {(x²-1)+y²+i2y}/{(x+1)²+y²}
Now,
arg ((z-1)/(z+1)) = arg [{(x²+y²-1)/(x+1)²+y²} + i {2y/(x+1)²+y²}]
⇒ π/2 = tan¯¹ {2y/(x²+y²−1)}
⇒ tan π/2 = {2y/(x²+y²−1)} [Using (i)]
⇒ 1/0 = {2y/(x²+y²−1)}
⇒ x² + y² = 1
Que-17: Find the amplitude of the complex number i sin (π/19)
Sol: Let z = i sin (π/19)
or z = 0 + i sin (π/19)
Let amplitude of z be θ then
sin θ= [{sin(π/19)} / {√0²+(sin π/19)²}]
or sin θ = {sin(π/19)}/{sin(π/19)} = 1
θ = π/2.
Que-18: If z is a complex number of unit modulus and argument θ, then show that arg {(1+z)/(1+z¯)} = θ
Sol: arg {(1+z)/(1+z¯)}
= arg {(1+z)/(1+(1/z))} [z¯ = 1/z]
= arg {(1/z)/{(z+1)/z}}
= arg {z(1+z)/(z+1)}
= arg (z)
= θ
Hence arg {(1+z)/(1+z¯)} = θ
–: End of Complex Numbers Class 11 OP Malhotra Exe-9D ISC Maths Ch-9 Solutions. :–
Return to :- OP Malhotra ISC Class-11 S Chand Publication Maths Solutions
Thanks
Please share with your friends


