Complex Numbers Class 11 OP Malhotra Exe-9E ISC Maths Solutions

Complex Numbers Class 11 OP Malhotra Exe-9E ISC Maths Solutions Ch-9. In this article you would learn about Locus Problems. Step by step solutions of latest textbook has been given as latest syllabus. Visit official Website CISCE for detail information about ISC Board Class-11 Mathematics.

Complex Numbers Class 11 OP Malhotra Exe-9E ISC Maths Solutions Ch-9

Board	ISC
Publications	S Chand
Subject	Maths
Class	11th
Chapter-9	Complex Numbers
Writer	O.P. Malhotra
Exe-9(E)	Locus Problems.

Exercise- 9E

Complex Number Class 11 OP Malhotra Exe-9E Solution.

Que-1: Illustrate in the complex plane, the set of points satisfying the following conditions. Explain your answer:
(i) |z| ≤ 3
(ii) arg (z – 2) = π/3
(iii) | i – 1 – 2z | > 9

Sol: (i) Let z = x + iy
∴ | z | ≤ 3 ⇒ | x + iy ≤ 3
⇒ x² + y² ≤ 9
which represents the set of points in interior and on the circle with centre (0, 0) and radius 3.

(ii) arg (z – 2) = π/3
⇒ arg (x + iy – 2) = π/3
⇒ tan¯¹ (y/(x−2)) = π/3
⇒ y/(x−2) = tan (π/3) = √3 ⇒ y = √3(x – 2)
which represents the set of points on line which intersects x-axis at (2, 0) and making an angle of 60° with +ve direction of x-axis.

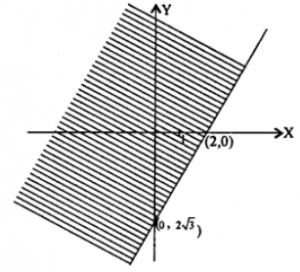
(iii) Given | i – 1 – 2z | > 9
| i – 1 – 2 (x + iy) | > 9, where z = x + iy

Que-2: Illustrate and explain the region of the Argand’s plane represented by the inequality |z + i| ≥ |z + 2|.

Sol: Let z = x + iy
given | z + i | ≥ | z + 2 |
⇒ | x + iy + i | ≥ | x + iy + 2 |
⇒ |x + i (y + 1) | ≥ |x + 2 + iy |
⇒ √(x²+(y+1)²) ≥ √((x+2)²+y²)
On squaring both sides ; we have
x² + (y + 1)² ≥ (x + 2)² + y²
⇒ x² + y² + 2y + 1 ≥ x² + 4x + 4 + y²
⇒ 2y + 1 ≥ 4x + 4
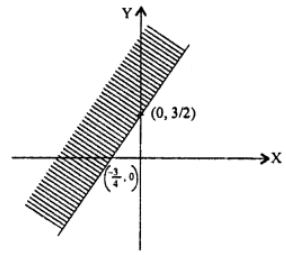
⇒ y ≥ 2x + (3/2)
which represents the set of points in the region lies above the line PQ intersects coordinate axes at (0, (3/2)) and (- (3/4), 0)

Que-3: Illustrate and explain the set of points z in the Argand diagram, which represents | z – z₁ | ≤ 3 where z1 = 3 – 2i

Sol: Given | z – z₁| ≤ 3 ;
where z₁ = 3 – 2i
⇒ | z – (3 – 2i) | ≤ 3
⇒ | x + iy – 3 + 2i | ≤ 3
⇒ | (x – 3) + i (y + 2) | ≤ 3
⇒ (x – 3)² + (y + 2)² ≤ 9
which represents the set of points in the interior and on the circle with centre (3, – 2) and radius 3.

Que-4: If z = x + yi and ω = (1−zi)/(z−i) then
| ω | = 1 implies that in the complex plane
(a) z lies on the imaginary axis
(b) z lies on the real axis
(c) z lies on the unit circle
(d) None of these

Sol: Given z = x + iy and w = (1−zi)/(z−i)
and |w| = 1 ⇒ ∣∣(1−zi)/(z−i)∣∣ = 1
⇒ |1 – zi | = |z – i| [∵ ∣∣ z1/z2 ∣∣ = |z1| / |z2| ]
⇒ | 1 – (x + iy) i | = | x + iy – i |
⇒ |1 – ix + y| = |x + i(y – 1)|
⇒ 1(1 + y) – ix| = | x + | 0 – 1) |
⇒ √((1+y)²+(-x)²) = √(x²+(y-1)²)
On squaring both sides ; we have
(1 + y)² + x² = x² + (y – 1)²
⇒ y² + 2y + 1 – x² = x²+y² – 2y + 1
⇒ 4y = 0
⇒ y = 0
which is the eqn. of x-axis. z lies on real axis i.e. x-axis

Que-5: Find the locus of a complex number z such that arg [(z−2)/(z+2)] = π/3.

Sol: Given : arg [(z−2)/(z+2)] = π/3.
= ar (z-2) – arg (z+2) = π/3
= arg (x+iy-2) – arg (x+iy+2) = π/3   [z = x+iy]
= arg (x-2+iy) – arg (x+2+iy) = π/3
tan¯¹ [y/(x-2)] – tan¯¹ [y/(z+2)] = π/3

Que-6: If the amplitude of z – 2 – 3i is π/4, then find the locus of z = x +yi.

Sol: Given z = x + iy
and amp (z – 2 – 3i) = π/4
⇒ amp (x + iy – 2 – 3 z) = π/4
⇒ amp [(x – 2) + i (y – 3)] = π/4
⇒ tan-1((y−3)/(x−2)) = π/4
⇒ y−3x−2 = tan π/4 = 1
⇒ y – 3 = x – 2
⇒ x – y + 1 = 0
Hence locus of z represents a straight line intersecting coordinate axes at (- 1, 0) and (0, 1).

Que-7: Find the locus of z if
ω = z/[z−(1/3)]i = 1.

Sol: Let z = x+iy

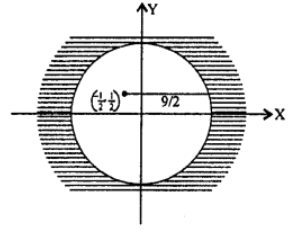
Que-8: Show that | (z-2)/(z-3) | = 2 represents a circle. Find its centre and radius.

Sol: We have | (z-2)/(z-3) | = 2
Putting z = x+iy

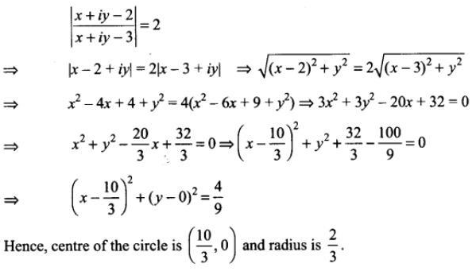
Que-9: Find the radius and centre of the circle zz¯+ (1 – i) z + (1 + i) z¯ – 7 = 0.

Sol: Given eqn. of circle be zz¯+(1 – i)z + (1 + i)z¯ – 7 = 0 …(1)
where z = x + iy and z¯ = x – iy
∴ eqn. (1) becomes ;
⇒ (x + iy) (x – iy) + (1 – i) (x + iy) + (i + i) (x – iy) – 7 = 0
⇒ x² + y² + x + iy – ix + y + x – iy + ix + y – 7 = 0
⇒ x² + y² + 2x + 2y – 7 = 0
⇒ (x² + 2x) + (y² + 2y) – 7 = 0
⇒ (x² + 2x + 1) + (y² + 2y + 1) – 9 = 0
⇒ (x + 1)² + (y + 1)² = 9
which represents a circle with centre (- 1, – 1) and radius 3.

Que-10: What is the region represented by the inequality 3 < | z – 2 – 3i|< 4 in the Argand plane.

Sol: Given 3 < |z – 2 – 3i| < 4;

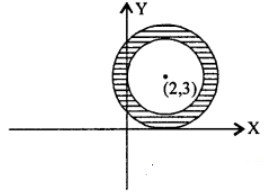
where z = x + iy
⇒ 3 < | x + iy – 2 – 3i| < 4
⇒ 3 < | (x – 2) + | (y – 3) | < 4
⇒ 3 < √{(x-2)²+(y-3)²} < 4
⇒ 9 < (x – 2)² + (y – 3)² <
which represents the set of points lies in the region between two concentric circles with centre (2, 3) and radius 2 and 3.

Que-11: If the real part of [(z¯+2)/(z¯-1)] is 4, then show that the locus of the point representing z in the complex plane is a circle. 

Sol: Let z = x + iy
∴ z¯ = x – iy
So (z¯+2)/(z¯-1) = (x-iy+2)/(x-iy-1)
= {(x+2)-iy}/{(x-1)-iy}
= [{(x+2)-iy}/{(x-1)-iy}] × {(x-1)+iy}/{(x-1)+iy}
= [(x+2)(x-1)+(x+2)yi-(x-1)yi-i²y²]/[(x-1)²-i²y²]
= [x²+2x-x-2+(x+2-x+1)yi+y²] / [(x-1)²+y²]
= [x²+y²+x-2]/[(x-1)²+y²] + [3y/{(x-1)²+y²i}]
Real part = 4
∴ [x²+y²+x-2]/[(x-1)²+y²] = 4
⇒ x² + y² + x – 2 = 4[(x – 1)² + y²]
⇒ x² + y² + x – 2 = 4[x² + 1 – 2x + y²]
⇒ x² + y² + x – 2 = 4x² + 4 – 8x + 4y²
⇒ x² – 4x² + y² – 4y² + x + 8x – 2 – 4 = 0
⇒ – 3x² – 3y² + 9x – 6 = 0
⇒ x² + y² – 3x + 2 = 0
Which represents a circle.
Hence, z lies on a circle.

–: End of Complex Numbers Class 11 OP Malhotra Exe-9E ISC Maths Ch-9 Solutions. :–

Return to :- OP Malhotra ISC Class-11 S Chand Publication Maths Solutions

Thanks

Please share with your friends