Complex Numbers Class 11 OP Malhotra Exe-9F ISC Maths Solutions

Complex Numbers Class 11 OP Malhotra Exe-9F ISC Maths Solutions Ch-9 Solutions. In this article you would learn about Square root of Complex Number and Cube root of unity. Step by step solutions of latest textbook has been given as latest syllabus. Visit official Website CISCE for detail information about ISC Board Class-11 Mathematics.

Complex Numbers Class 11 OP Malhotra Exe-9F ISC Maths Solutions Ch-9

Board	ISC
Publications	S Chand
Subject	Maths
Class	11th
Chapter-9	Complex Numbers
Writer	O.P. Malhotra
Exe-9(F)	Square root of Complex Number and Cube root of unity.

Exercise- 9F

Complex Number Class 11 OP Malhotra Exe-9F Solution.

Que-1: Find the square root of the following complex numbers.
(i) 3 + 4i
(ii) – 8 + 6i
(iii) – 40 – 42i
(iv) i
(v) [{(2+3i)/(5−4i)}+{(2−3i)/(5−4i)}]

Sol: (i) √(3+4i) = x + iy; where x, y ∈ R
On squaring both sides ; we have
3 + 4i = (x + iy)²
⇒ 3 + 4i = x² – y² + 2ixy
On comparing real and imaginary parts on both sides ; we have
x² – y² = 3 …(1)
and 2xy = 4 …(2)
∴ x² + y² = √{(x²-y²)²+(2xy)²}
= √(3²+4²) = 5 … (3)
On adding (1) and (3); we have
2x² = 8 ⇒ x² = 4 ⇒ x = ± 2
eqn. (3) – eqn. (1) gives ;
2y² = 2 ⇒ y = ± 1
Since xy be +ve
∴ x and y both are of same sign
Hence x = 2, y = 1 or x = – 2, y = – 1
∴ √(3+4i) = 2 + i or – (2 + i)

(ii) √(-8+6i) = x + iy where x, y ∈ R
On squaring both sides ; we have
– 8 + 6i = (x + iy)² = x² – y² + 2ixy
On ωmparing real and imaginary parts on both sides, we get
x² – y² = – 8 … (1)
and 2xy = 6 … (2)
Now x² + y² = √{(x²-y²)²+(2xy)²}
= √{(-8²)+6²}
= √(64+36) = 10 … (3)
On adding (1) and (3) ; we have
2x² = 2 ⇒ x = ± 1
eqn. (3) – eqn. (1) gives ;
2y² = 18 ⇒ y² = 9 ⇒ y = ± 3
Since xy be +ve ∴ both x and y are of same sign.
∴ x = 1; y = 3 or x = – 1, y = – 3
Thus √(-8+6i) = 1 + 3i or – (1 + 3i)

(iii) √(-40+42i) = x – iy where x, y ∈ R
On squaring both sides ; we have
– 40 – 42i = (x – iy)² = x² – y² – 2ixy
On comparing real and imaginary parts on both sides ; we have
– 40 = x² – y² …(1)
and 2xy = 42 …(2)
Now x² + y² = √{(x²-y²)²+(2xy)²}
= √{(-40)²+42²}
= √(1600+1764)
= √3264 = 58 … (3)
On adding (1) and (3) ; we have
2x² =18 ⇒ x = ± 3
eqn. (3) – eqn. (1) gives ;
2y² = 98 ⇒ y² = 49 ⇒ y = ± 7
Since xy be of +ve sign ∴ both x and y are of same sign
i.e. when x = 3, y = 7 or x = – 3, y = – 7
Thus, √(-40+42i)
= 3 – 7i or – 3 + 7i
= ±(3 – 7i)

(iv) Let √i = x + iy;
On squaring; we have i = (x + iy)² = x² – y² + 2ixy
On comparing real and imaginary parts on both sides, we have
x² – y² = 0 …(1)
and 2xy = 1 …(2)
∴ x² + y² = √{(x²-y²)²+(2xy)²}
= √(0²+1²) = 1 … (3)
On adding eqn. (1) and eqn. (3); we have

Que-2: If ω is a cube root of unity, then
(i) ω + ω² = ….
(ii) 1 + ω = …
(iii) 1 + ω³ = ….
(iv) ω³ = ….

Sol: Now ω be the cube root of unity
∴ ω = (−1+√3i)/2 and ω² = (−1−√3i)/2
(i) 1 + ω² = {(−1+√3i)/2} + {(−1−√3i)/2}
= −2/2 = – 1

(ii) 1 + ω = 1 + {(−1+√3i)/2}
= (2−1+√3i)/2
= (1+√3i)/2 = – ω²

(iii) 1 + ω² = 1 + {(−1−√3i)/2}
= (2−1−√3i)/2
= (1−√3i)/2
= [−{(−1+√3i)/2}] = – ω

(iv) ω³ = ω². ω = ((−1−√3i)/2) ((−1+√3i)/2)
= {(−1)²−(√3i)²}/4
= (1+3)/4 = 1

Que-3: If 1, ω, ω² are three cube roots of unity, prove that
(i) (1 + ω²)4 = ω
(ii) (1 + ω – ω²)³ = (1 – ω + ω²)³ = – 8
(iii) (1 – ω) (1 – ω²) = 3
(iv) {1/(1+ω)} + {1/(1+ω²)} = 1

Sol: (i) (1 + ω²)4 = (- ω)4= ω³ . ω = ω [∵ 1 + ω + ω² = 0 and ω³ = 1]

(ii) (1 + ω – ω²)² = (- ω² – ω²)³
= (- 2ω²)³ = – 8ω^6
= – 8 (ω³)² = – 8
and (1 – ω + ω²)³ = (- ω – ω)³
= (- 2ω)³ = – 8ω³
= – 8 x 1 = – 8 [∵ 1 + ω + ω² = 0 and ω³ = 1]

(iii) (1 – ω) (1 – ω²) = 1 – ω – ω² + ω³
= 1 – (ω + ω²) + 1 [∵ ω³ = 1]
= 1 – (- 1) + 1 [∵ 1 + ω + ω² = 0]
= 1 + 1 + 1 = 3

(iv) {1/(1+ω)} + {1/(1+ω²)} = (1/−ω²) + (1/−ω) [∵ 1 + ω + ω² = 0]
= (1+ω)/−ω² = −ω²/−ω² = 1

Que-4: (i) (1 – ω – ω²)⁶ = 64
(ii) (1 + ω – ω²) (1 – ω + ω²) = 4

Sol: (i) (1 – ω – ω²)⁶ = [1 – (ω + ω²)]⁶ = [1 – (- 1)]⁶ = 2⁶ = 64 [∵ 1 + ω + ω² = 0]

(ii) (1 + ω – ω²) (1 – ω + ω²) = (- ω² – ω²) (- ω – ω) [∵ 1 + ω + ω² = 0]
= (- 2ω²) (- 2ω)
= 4ω³
= 4 x 1 = 4

Que-5: (3 + 5ω + 3ω²)⁶ = (3 + 5ω² + 3ω)⁶ = 64

Sol: (3 + 5ω + 3ω²)⁶ = (3 + 5ω² + 3ω)⁶
= [3 (- ω) + 5ω]⁶ [∵ 1 + ω + ω² = 0]
= (2ω)⁶ = 64 (ω³)² = 64
and (3 + 5ω² + 3ω)⁶ = [3 (1 + ω) + 5ω²]⁶ = [3 (- ω²) + 5ω²]⁶ [∵ 1 + ω + ω² = 0]
= (2ω²)⁶ = 64ω¹² = 64 (ω³)⁴ = 64 [∵ ω³ = 1]

Que-6: ω²⁸ + ω²⁹ + 1 = 0

Sol: ω²⁸ + ω²⁹ + 1 = (ω³)⁹ . ω + (ω³)⁹ . ω² + 1
= 1⁹ . ω + 1⁹ . ω² + 1 [∵ ω³ = 1]
= ω + ω² + 1 = 0

Que-7: Prove that {(−1+i√3)/2}^n + {(−1−i√3)/2}^n is equal to 2 if n be a multiple of 3 and is equal to – 1 if n be any other integer.
Or
If 1, ω, ω² are the cube roots of unity, prove that ωn + ω2n = 2 or – 1 acωrding as n is a multiple of 3 or any other integer.

Sol: We know that cube root of unity are 1, ω, ω²
where ω = (−1+√3i)/2 and ω² = (−1−√3i)/2
∴ {(−1+i√3)/2}^n + {(−1−i√3)/2}^n
= ω^n + (ω²)^n
= ωn+ω²^n
Case-I : When n be a multiple of 3
∴ n = 3k
∴ ωⁿ + ω²ⁿ = ω^3k + ω^6k = (ω³) + (ω³)^2k = 1^k + 1^2k =1 + 1 = 2

Case-II : When n be not a multiple of 3
∴ n = 3k + 1, 3k + 2

Subcase – I : When n = 3k + 1
ωⁿ + ω²ⁿ = ω^3k+1 + ω^2(3k+1) = ω^3k . ω + ω^6k . ω²
= 1 . ω + 1 . ω² = ω + ω² = – 1 [∵ ω + ω² +1 = 0 and ω^3k = (ω³)^k = 1]

Subcase-II : When n = 3k+2
∴ ωⁿ + ω²ⁿ = ω^3k+1 + ω^2(3k+2) = ω^3k. ω² + ω^6k + ω⁴ = (ω³)^k ω² + (ω³)^2k . ω³ . ω
= ω² + ω = – 1 [∵ (ω³)^k = 1^k = 1]
Thus, ωⁿ + ω²ⁿ = 2 or – 1
according as n is a multiple of 3 or any other integer.

Prove the following:

Que-8: (1 – ω + ω²) (1 + ω – ω²) (1 – ω – ω²) = 8.

Sol: (1 – ω + ω²) (1 + ω – ω²) (1 – ω – ω²)
= (1 + ω² – ω) (1 + ω – ω²) (1 – (ω + ω²))
= (- ω – ω) (- ω² – ω²) (1 – (- 1)) [∵ 1 + ω + ω² = 0]
= (- 2ω) (- 2ω²)² = 8ω³
= 8 [∵ ω³ = 1]

Que-9: (i) (1 + ω) (1 + ω²) (1 + ω⁴) (1 + ω⁸) …. to 2n factors = 1
(ii) (1 – ω + ω²) (1 – ω² + ω⁴) (1 – ω⁴ + ω⁸)…… to 2n factors = 2²ⁿ.

Sol: (i) L.H.S = (1 + ω) (1 + ω²) (1 + ω⁴) (1 + ω⁸) …. to 2n factors
= (1 + ω) (1 + ω²) (1 + ω³ . ω) (1 + ω⁶ . ω²) … 2n factors
= (1 + ω) (1 + ω²) (1 + ω) (1 + ω²) …. 2n factors
= (1 + ω)ⁿ (1 + ω²)ⁿ = [(1 + ω) (1 + ω²)]ⁿ
= [1 + ω + ω² + ω³]ⁿ = [0 + 1]ⁿ = 1ⁿ = 1 [∵ 1 + ω + ω² = 0 and ω³ = 1]

(ii) (1 – ω + ω²) (1 – ω² + ω⁴) (1 – ω⁴ + ω⁸) to 2n factors
= (1 – ω + ω²) (1 – ω² + ω³ . ω) (1 – ω³ . ω + ω⁶ . ω²) to 2n factors
= (1 – ω + ω²) (1 – ω² + ω) (1 – ω + ω²)…. 2n factors [∵ ω³ = 1]
= [(1 – ω + ω²) …. n factors] [(1 – ω² + ω) …. n factors
= (- 2ω)ⁿ (- 2ω²)ⁿ [∵ 1 + ω + ω² = 0]
= 2ⁿ (ω . ω²)ⁿ (- 1)²ⁿ
= 2²ⁿ (ω³)ⁿ
= 2²ⁿ1ⁿ
= 2²ⁿ

Que-10: (a+bω+cω²)/(b+cω+aω²) = ω

Sol: LHS = (a+bω+cω²)/(b+cω+aω²)
= (aw³+bw+cw²)/(b+cw+aw²)
= {w(aw²+cw+b)} / (aw²+cw+b)
= w = RHS.

Que-11: {(a+bω+cω²)/(c+aω+bω²)} + {(a+bω+cω²)/(b+cω+aω²)} = – 1

Sol: LHS = {(a+bω+cω²)/(c+aω+bω²)} + {(a+bω+cω²)/(b+cω+aω²)}

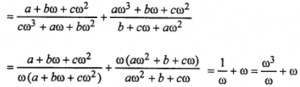
= w² + w = -1

Que-12: If ω is a cube root of unity and n is a positive integer which is not a multiple of 3, then show that (1 + ωⁿ + ω²ⁿ) = 0.

Sol: When n is not a multiple of 3
∴ n be of the form 3k + 1 or 3k + 2
Case – I. When n = 3k + 1
1 + ωⁿ + ω²ⁿ = 1 + ω^3k+1 + ω^6k+2
= 1 + (ω³)^k ω + (ω³)^2k . ω²
= 1 + 1^k . ω + 1^2k ω²
= 1 + ω + ω² = 0

Que-13: Show that (x + ωy + ω²z) (x + ω²y + ωz) = x² + y² + z² – yz – zx – xy.

Sol: L.H.S = (x + ωy + ω²z) (x + ω²y + ωz)
= x² + (ω² + ω) xy + xz (ω + ω²) + ω³y² + yz (ω² + ω⁴) + ω³z²
= x² – xy + xz(- 1) + y² + yz (- 1) + z² [∵ 1 + ω + ω² = 1]
= x² + y² + z² – xy – yz – zx = R.H.S

Que-14: Show that x³ + y³ = (x + y) (ωx + ω²y) (ω²x + ωy).

Sol: R.H.S = (x + y) (ωx + ω²y) (ω²x + ω²y) = (x + y) (ω³x² + ω²xy + ω⁴xy + ω³y²)
= (x + y) [1 . x² + xy (ω² + ω³ . ω) + 1 . y²] [∵ ω³ = 1]
= (x + y) (x² + xy (ω² + ω) + y²) = (x + y) (x² – xy + y²) [∵ 1 + ω + ω² = 1]
= x³ + y³ = L.H.S

Que-15: If 1, ω, ω² are cube roots of unity, prove that 1, ω² are vertices of an equilateral triangle.

Sol: Since 1, ω and ω² are the cube root of unity.
where ω = (−1+√3i)/2 and ω² = (−1−√3i)/2

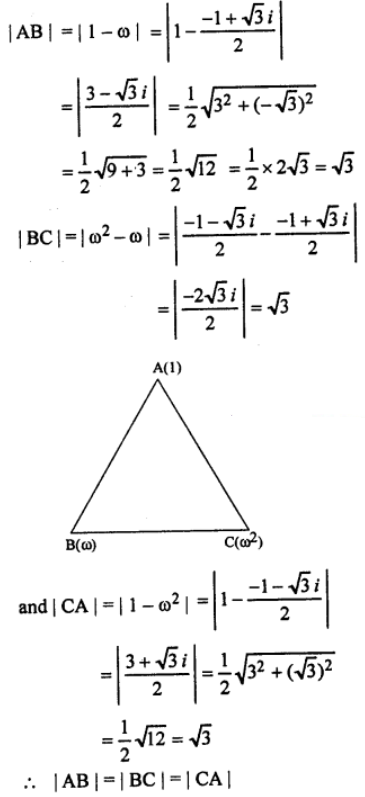
Thus, 1, ω and ω² are the vertices of an equilateral triangle.

–: End of Complex Number Class 11 OP Malhotra Exe-9F ISC Math Ch-9 Solution :–

Return to :- OP Malhotra ISC Class-11 S Chand Publication Maths Solutions

Thanks

Please share with your friends