Compound and Multiple Angles Class 11 OP Malhotra Exe-5A ISC Maths Solutions Ch-5 Solutions. In this article you would learn about The Addition Formulae. Step by step solutions of latest textbook has been given as latest syllabus. Visit official Website CISCE for detail information about ISC Board Class-11 Mathematics.

Compound and Multiple Angles Class 11 OP Malhotra Exe-5A ISC Maths Solutions Ch-5

Board	ISC
Publications	S Chand
Subject	Maths
Class	11th
Chapter-5	Compound and Multiple Angles
Writer	OP Malhotra
Exe-5(A)	The Addition Formulae.

Exercise- 5A

Compound and Multiple Angles Class 11 OP Malhotra Exe-5A Solution.

Que-1: Compute :
(i) sin 15° from the functions of 60° and 45°,
(ii) cos 345° from the functions of 300° and 45°,
(iii) tan 105° from the functions of 45° and 60°,
(iv) sin 135° from the functions of 180° and 45°,
(v) cos 195° from the functions of 150° and 45°,
(vi) cosec (13π/12)

Sol: (i) sin 15° = sin (60° – 45°)
= sin 60° cos 45° – cos 60° sin 45°
= (√3/2) × (1/√2) − (1/2) × (1/√2)
= (√3−1)/2√2 [∵ sin (A – B) = sin A cos B – cos A sin B]

(ii) cos 345° = cos (300° + 45°)
= cos 300° cos 45° – sin 300° sin 45°
= cos (270° + 30°) (1/√2) – sin (270° + 30°) (1/√2)
= sin30° x (1/√2) + cos30° x (1√2) [∵ cos (270° + θ) = cos θ and sin (270° + θ) = – cos θ]
= {1/2√2} + {√3/2√2}
= {√3+1}/2√2

(iii) tan 105° = tan (60° + 45°)
= {tan60° + tan45°}/{1−tan60°tan45°}
= {√3+1}/{1−√3} [∵ tan (A + B) = {tanA+tanB}/{1−tanAtanB} ]
= {(√3+1)/(1−√3)} × {(1+√3)/(1+√3)}
= {3+1+2√3}/{1−3}
= (4+2√3)/−2
= −(2+√3)

(iv) sin 135° = sin (180°- 45°)
= sin 180° cos 45° – cos 180° sin 45°
= 0 x (1/√2) − (−1)(1/√2)
= 1√2.

(v) cos 195° = cos (150° + 45°)
= cos 150° cos 45° – sin 150° sin 45°
= cos (180°- 30°) cos 45° – sin (180°- 30°) sin 45°
= – cos 30° cos 45° – sin 30° sin 45°
= (√3/2) × (1/√2) − (1/2) × (1/√2)
= −{(√3+1)/2√2}

(vi) cosec (13π/12) = cosec (π+(π/12))
= -cosec π/12

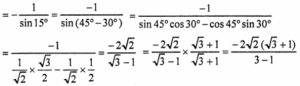
= -√2 (√3+1)
= -√6 – √2.

Que-2: Simplify by reducing to a single term :
(i) sin 3α cos 2α + cos 3α sin 2α
(ii) cos 5θ cos 2θ – sin 5θ sin 2θ.
(iii) sin 22° cos 38° + cos 22° sin 38°.
(iv) sin 80° cos 20° – cos 80° sin 20°.
(v) sin (x – y) cos x – cos (x -y) sin x.
(vi) cos (θ + α) cos (θ – α) – sin (θ + α) sin (θ – α)
(vii) {tan69°+tan66°}/{1−tan69°tan66°}
(viii) {tanα−tan(α−β)}/{1+tanα tan(α−β)}.

Sol:  (i) sin 3α cos 2α + cos 3α sin 2α
= sin (3α + 2a)
= sin 5a [∵ sin A cos B + cos A sin B = sin (A + B)]

(ii) cos 5θ cos 2θ – sin 5θ sin 2θ
= cos (5θ + 2θ)
= cos 7θ [∵ cos A cos B – sin A sin B = cos (A + B)]

(iii) sin 22° cos 38° + cos 22° sin 38°
= sin (22° + 38°)
= sin 60° = √3/2

(iv) sin 80° cos 20° – cos 80° sin 20°
= sin (80° – 20°)
= sin 60° = √3/2

(v) sin (x – y) cos x – cos (x – y) sin x
= sin (x – y – x)
= sin (- y)
= – sin y [∵ sin A cos B – cos A sin B = sin (A – B)]

(vi) cos (θ + α) cos (θ – α) – sin (θ + α) sin (θ – α) = cos (θ + α + θ – α) = cos 2θ [∵ cos A cos B – sin A sin B = cos (A + B)]

(vii) {tan69°+tan66°}/{1−tan69°tan66°}
= tan (69° + 66°)   [∵ tan (a + b) = {tanA+tanB}/{1−tanAtanB}]
= tan 135°
= tan (180° – 45°)
= – tan 45° = – 1

(viii) {tanα−tan(α−β)}/{1+tanα tan(α−β)}
= tan [α – (α – ß)]
= tan ß    [∵ {tanA−tanB}/{1+tanAtanB} tan (A – B)]

Prove that :

Que-3: (sin α cos ß + cos α sin ß) + (cos α cos ß – sin α sin ß)² = 1.

Sol: L.H.S = (sin α cos ß + cos α sin ß)² + (cos α cos ß – sin α sin ß)²
= sin² (α + ß) + cos² (α + ß)
= 1 = R.H.S.

Que-4: sin (60° + θ) – sin (60° – θ) = sin θ.

Sol: sin (60° + θ) – sin (60° – θ)
= sin 60° cos θ + cos 60° sin θ – sin 60° cos θ + cos 60° sin θ
= 2 cos 60° sin θ
= 2 x (1/2) sin θ = sin θ

Que-5: sin (θ + 30°) + cos (θ + 60°) = cos θ.

Sol: L.H.S = sin (θ + 30°) + cos (θ + 60°)
= sin θ cos 30° + cos θ sin 30° + cos θ cos 60° – sin θ sin 60°
= sin θ x (√3/2) + (cosθ/2) + cos θ x (1/2) – (√3/2) sin θ
= cos θ = R.H.S.

Que-6: sin (240° + θ) + cos (330° + θ) = 0.

Sol: L.H.S. = sin (240° + θ) + cos (330° + θ)
= sin (180° + 60° + θ) + cos (360° – 30° + θ)
= – sin (60° + θ) + cos [360° – (30° – θ)]
= – sin (60° + θ) + cos (30° – θ) [∵ sin (180° + θ)
= – sin θ ; cos (360° – θ) = cos θ]
= – sin 60° cos θ – cos 60° sin θ + cos 30° cos θ + sin θ sin 30°
= – (√3/2) cos θ – (1/2) sin θ + (√3/2) cos θ + (1/2) sin θ
= 0 = R.H.S.

Que-7: sin (A – 45°) = 1/√2 (sin A – cos A).

Sol: sin (A – 45°)
= sin A cos 45° – cos A sin 45°
= (sinA/√2) − (cosA/√2)
= (1/√2) (sin A – cos A)

Que-8: cos((π/3)+x) = (cosx−√3sinx)/2.

Sol:   cos((π/3)+x)
= cos(π/3) cosx – sin(π/3) sinx
= (1/2)cos x – (√3/2)sin x
= {cosx – √3sinx}/2.

Que-9: (i) tan (45° + θ) = (1+tanθ)/(1−tanθ)
(ii) tan (45° – θ) = (1−tanθ)/(1+tanθ).

Sol:  (i) tan (45° + θ)
= {tan45° + tanθ}/{1 – tan45° tanθ}
= {1+tanθ}/{1-tanθ}.

(ii) tan (45° – θ)
= {tan45° – tanθ}/{1 + tan45° tanθ}
= {1-tanθ}/{1+tanθ}.

Que-10: (i) {sin(θ+ϕ)}/{sinθcosϕ} = cot θ tan Φ + 1.
(ii) {sin(θ−ϕ)}/{sinθ sinϕ} = cot Φ – cot θ.

Sol: (i) {sin(θ+ϕ)}/{sinθcosϕ}
= {sinθcosϕ + cosθsinϕ}/{sinθcosϕ}
= {sinθcosϕ/sinθcosϕ} + {cosθsinϕ/sinθcosϕ}
= 1 + cotθ tanϕ

(ii) {sin(θ−ϕ)}/{sinθ sinϕ}
= {sinθcosϕ−cosθsinϕ}/{sinθ sinϕ}
= {sinθcosϕ/sinθsinϕ} − {cosθsinϕ/sinθsinϕ}
= cotϕ−cotθ.

Que-11: [{sin(A−B)}/{sinA sinB}] + [{sin(B−C)}/{sinB sinC}] + [{sin(C−A)}/{sinC sinA}] = 0.

Sol: LHS = [{sin(A−B)}/{sinA sinB}] + [{sin(B−C)}/{sinB sinC}] + [{sin(C−A)}/{sinC sinA}]
= [{(sinA cosB)-(cosA sinB)}/(sinA sinB)] + [{(sinB cosC)-(cosB sinC)}/(sinB sinC)] + [{(sinC cosA)-(cosc sinA)}/(sinC sinA)]
= cotB – cotA + cotC – cotB + cotA – cotC
= 0 RHS.

Que-12: sin 105° + cos 105° = cos 45°.

Sol: L.H.S. = sin 105° + cos 105°
= sin (60° + 45°) + cos (60° + 45°)
= sin 60° cos 45° + cos 60° sin 45° + cos 60° cos 45° – sin 60° sin 45°
= (√3/2) × (1/√2) + (1/2) × (1/√2) + (1/2) × (1/√2) − (√3/2) × (1/√2)
= 2/2√2
= 1/√2
= cos 45° = R.H.S.

Que-13: Find the value of sin (α + ß), cos (α + ß), and tan (α + ß), given
(i) sin α = (3/5), cos ß = (5/13), α and ß in Quadrant I.
(ii) cos α = (−12/13), cot ß = (24/7), α in Quadrant II, ß in Quadrant III.

Sol: (i) alpha lies in quadrant two
cosα= -12/13
=> Sinα = + Ve as in 2nd Quadrant Sin is + Ve
Sin²α = 1 – Cos²α
=> Sinα = 5/13
=> tanα =Sinα  /cosα =   – 5/12
cotβ=24/7    =>  tanβ = 7/24
Sinβ = -7/25
cosβ = – 24/25
Sin(α – β)  = SinαCosβ – CosαSinβ
= (5/13)(-24/25)  – (-12/13)(-7/25)
= -120/325  – 84/325
= -204/325
Cos(α – β)  = CosαCosβ + SinαSinβ
= (-12/13)(-24/25)  + (5/13)(-7/25)
= 288/325  – 35/325
= 253/325
tan(α – β)
= Sin(α – β) / Cos(α – β)
= – 204/253

(ii) since α lies in IInd quadrant
∴ sin α > 0
given cos α = -12/13
sin α = √(1-cos²α)
= √{1-(-12/13)}²
sin α = √{1-(144/169)} = 5/13
Since β lies in IIIrd quadrant
∴ sin β, cos β < 0.
given cos β = 24/7
cosec β = -√(1+cot²β)
= -√{1+(24/7)}²
cosec β = -√{625/49} = -25/7
Sin (α + β)  = SinαCosβ + CosαSinβ
= {(5/13)(-24/25)} + {(-12/13)/(-7/25)}
= (-120/325) – (84/325)
= -36/325
Cos(α + β)  = CosαCosβ – SinαSinβ
= {(-12/13)/(-24/25)} – {(5/13)(-7/25)}
= (288+35)/325
= 323/325
tan (α + β) = {Sin (α + β)}/{Cos(α + β)}
= {-36/325}/{323/325}
= -36/323.

Que-14: Find the values of sin (α – ß), cos (α – ß) and tan (α – ß), given
(i) sin α = (8/17). tan ß = (5/12), α and ß in Quadrant I.
(ii) cos α = (−12/13), cot ß = (24/7), α in Quadrant II, ß in Quadrant I.

Sol:  (i) Given : Alpha ( α ) and Beta ( β ) lie in first quadrant.
sin α = 8/17
tan β = 5/12
tan β = 5/12
Hence, opposite = 5 and adjacent = 12
sin ( α – β ) = sin α × cos β – cos α × sin β
→ sin ( α – β ) = 8/17 × 12/13 – 15/17 × 5/13
→ sin ( α – β ) = 96/221 – 75/221
→ sin ( α – β ) = 21/221
cos ( α – β ) = cos α × cos β + sin α × sin β
→ cos ( α – β ) = 15/17 × 12/13 + 8/17 × 5/13
→ cos ( α – β ) = 180/221 + 40/221
→ cos ( α – β ) = 220/221
→ tan ( α – β ) = tan α – tan β / 1 + tan α × tan β
→ tan ( α – β ) = 8/15 – 5/12 / 1 + 8/15 × 5/12
→ tan ( α – β ) = 96/180 – 75/180 / 1 + 8/15 × 5/12
→ tan ( α – β ) =21/180 / 1 + 40/180
→ tan ( α – β ) = 21/180 / 220/180
→ tan ( α – β ) = 21/220

(ii) Given : cos α = (−12/13), cot ß = (24/7)
sin(α−β) = (5/13​)(24/25​) − (−12/13​)(7/​25)
= (120/325) ​+ (84/325)
​= 204/325
cos(α−β) = (−12/13​)(24/25​) + (5/13​)(7/25​)
= (−288/325​) + (35/325)
​= −253/325
tan(α−β) = [{(-5/12)-(7/24)}]/[1+{(-5/12)(7/24)}]
= {(-10/24)-(7/24)}/{1-(35/288)}
= (-17/24)/(253/288)
= (-17/24) (288/253)
= -4896/6072
= -204/253.​

Que-15: If A and B are acute angles, find (A + B) given
(i) sin A = 1/√5, sin B = 1/√10.
(ii) tan A = 5/6, tan B = 1/11

Sol: Given A and B are acute angles
∴ cos A, cos B > 0
(i) sin A = 1/√5,
cos A = √{1-sin² A}
= √{1-(1/√5)²}
= √{1-(1/5)}
= √(4/5)
cos A = 2/√5 and sin B = 1/√10
cos B = √{1-sin²B}
= √{1-(1/10)²} = 3/√10
sin (A+B) = sin A cos B + cos A sin B
= (1/√5) × (3/√10) + (2/√5) × (1/√10)
= 5/√50
= 5/5√2 = 1/√2
= cos (A + B) = 1/√2
= A + B = cos¯¹ (1/√2)
= A + B = π/4
= A + B = 45°.

(ii)  Given : tan A = 5/6, tan B = 1/11
tan (A+B) = {tanA+tanB}/{1-tanA tanB}
= {(5/6)+(1/11)}/{1-(5/6)(1/11)}
= {61/66}/{61/66}
= 1
tan (A+B) = 1
A+B = tan¯¹ 1
A+B = π/4
A+B = 45°.

Que-16: Given that tan α = {m/(m+1)}, tan ß = {1/(2m+1)} then is the value of α + ß?

Sol: As given, tanα = m/(m+1)​
and tanβ = 1/(2m+1)​
tan(α+β) = (tanα+tanβ)/(1-tanα tanβ)​
= [{m/(m+1)} + {1/(2m+1)}]/[1-{m/(m+1)}×{1/(2m+1)}]
= {m(2m+1)+m+1}/{(m+1)(2m+1)-m}
= {2m²+2m+1}/{2m²+2m+1}
= 1
So, α+β = π/4

Que-17: In the ∆ABC, the foot of the perpendicular from A to BC is D. Given that tan B = (4/3), cos C = (15/17) and that AB = 20 cm, calculate without using tables.
(i) the lengths of the sides AC and BC ; (ii) the value of sin A.

Sol:  (i) Given tan ß = (4/3) ; cos C = (15/17) and AB = 20 cm

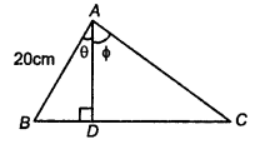
since tan ß = 4/3
⇒ AD/BD = 4/3
⇒ AD = 4k; BD = 3k
Since In ∆ADB, using pythagoras theorem,
AB² = AD² + BD²
⇒ 20² = (4k)² + (3k)²
⇒ 400 = 25k²
⇒ k² = 400/25 = 16
⇒ k = 4
∴ AD = 16 ; BD = 12
Since cos C = 15/17 = DC/AC
⇒ DC = 15x ; AC = 17x
In ∆ADC, AC² = AD² + DC²
⇒ (17x)² = 16² + (15x)²
⇒ 289 x² – 225 x² = 256
⇒ 64x² = 256
⇒ x² = 4
⇒ x = 2
∴ AC = 17x = 17 x 2 = 34 and DC = 15 x 2 = 30
and BC = BD + DC = 12 + 30 = 42 cm.

(ii) From figure,
sin θ = BD/AC = 12/20 = 3/5 and
cos θ = √{1-(9/25)} = 4/5
= sin Φ = CD/AC = 30/34 = 15/17  and
cos Φ = √{1-(225/289)} = 8/17
sin A = sin(θ+Φ) = sin θ cos Φ + cos θ sin Φ
= (3/5)×(8/17) + (4/5)×(15/17)
= (24+60)/85
= 84//85.

Que-18: Given that tan (A + B) = 1 and tan (A – B) = (1/7), find without using tables the values of tan A and tan B.

Sol:  Given tan (A + B) = 1 ⇒ {tanA+tanB}/{1−tanA tanB} = 1
⇒ tan A + tan B = 1 – tan A tan B … (1)
Also, tan (A – B) = 1/7
⇒ {tanA−tanB}/{1+tanA tanB} = 1/7
⇒ 7 (tan A – tan B) = 1 + tan A tan B … (2)
On adding (1) and (2); we have
8 tan A – 6 tan B = 2
⇒ 4 tan A – 3 tan B = 1 … (3)
From (1) and (2); we have
tan A + {4tanA−1}/3 = 1 – tan A{(4tanA−1/3)}
⇒ 3 tan A + 4 tan A – 1 = 3 – 4 tan² A + tan A
⇒ 4 tan² A + 6 tan A – 4 = 0
⇒ 2 tan² A + 3 tan A – 2 = 0
∴ tan A = {−3±√(9+16)}/4
= (−3±5)/4 = 1/2,−2
When tan A = 1/2 ∴ from (3); we have tan B = {4tanA−1}/3
= {2−1}/3 = 1/3
When tan A = – 2 ∴ from (3); tan B = – 3

Que-19: If tan (A + B) = x and tan B = (1/2) prove that tan A = (2x-1)/(x+2)  and obtain an expression for tan (A – B) in terms of x. If tan (A – B) = (1/3) and A is acute, find A without using tables.

Sol: Tan(A + B) = [tan(A) + tan(B)] / [1 – tan(A)tan(B)]
But, tan(A + B) = x, so replacing tan(A + B) with x, we get
x = [tan(A) + tan(B)] / [1 – tan(A)tan(B)]
But we’re given tan(B) = 1/2, so replacing every occurrence of tan(B) with (1/2), we get
x = [tan(A) + (1/2)] / [1 – tan(A)(1/2)]
Let’s simplify this complex fraction by multiplying top and bottom by 2.
x = [2tan(A) + 1] / [2 – tan(A)]
Now, we solve for tan(A) algebraically. Multiply both sides by
[2 – tan(A)], to obtain
x[2 – tan(A)] = 2tan(A) + 1. Expanding the left hand side,
2x – xtan(A) = 2tan(A) + 1
Now, move everything with a tan(A) to the right hand side; everything else, to the left hand side.
2x – 1 = 2tan(A) + xtan(A)
Factor tan(A) on the right hand side.
2x – 1 = tan(A) [2 + x]
Divide both sides by (2 + x)
tan(A) = (2x – 1) / (2 + x)
2) Find tan(A – B) in terms of x.tan(A – B) = [tan(A) – tan(B)] / [1 + tan(A)tan(B)]
Substituting tan(A) = (2x – 1) / (2 + x) and tan(B) = (1/2)
= [(2x – 1)/(2 + x) – (1/2)] / [1 + (1/2)(2x – 1)/(2 + x)]
Multiply top and bottom by 2(2 + x), to get rid of all fractions.
= [(2x – 1)(2) – (2 + x)] / [2(2 + x) + (2x – 1)(1/2)(2)]
= [4x – 2 – 2 – x] / [4 + 2x + 2x – 1]
= [3x – 4] / [4x + 3]
= 9x-12 = 4x-3
5x = 15
x = 3
tan A = {(2)(3)-1}/(2+3)
= 5/5 = 1
A = π/4.

Que-20: If sin (α + ß) = 4/5, sin(α – ß) = 5/13, α + ß, α – ß being acute angles prove that tan 2α = 63/16.

Sol: Given sin (α + ß) = 4/5 and sin (α – ß) = 5/13 since α + ß, α – ß are acute angles

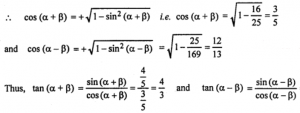
= (5/13)/(12/13)
= 5/12
tan 2α = {tan(α+ß)+tan(α-ß)}/{1-tan(α+ß)(tanα-ß)}
= {(4/3)+(5/12)}/{1-(4/3)(5/12)}
= {(48+15)/36}/{(36-20)/36}
= 63/16

Que-21: Prove that 1 + tan 2θ tan P = sec 2θ.

Sol: L.H.S = 1 + tan 2θ tan θ
= 1 + (sin2θ/cos2θ) ⋅ (sinθ/cosθ)
= {(cos2θ cosθ) + (sin2θ sinθ)}/cos2θ cosθ
= {cos(2θ−θ)}/cos2θ cosθ
= cosθ/cos2θ cosθ
= sec 2θ = R.H.S

Que-22: 4sin((π/3)−θ)sin((π/3)+θ) = 3 – 4 sin²θ.

Sol: 4sin((π/3)−θ)sin((π/3)+θ)

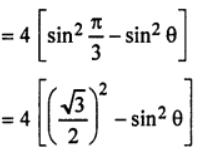
= 4[(3/4) – sin²θ]
= 3 – 4sin²θ.

Que-23: (cos17°+sin17°)/(cos17°−sin17°) = tan 62°.

Sol: LHS = (cos17°+sin17°)/(cos17°−sin17°)
Divide Numerator and Denominator by cos17° ; we have
= (1+tan17°)/(1-tan17°)
= (tan45°+tan17°)/(1-tan45° tan17°)
= tan (45°+17°)
= tan 62°
= RHS.

Que-24: tan 3A – tan 2A – tan A = tan 3A tan 2 A tan A.

Sol: tan 3A = tan (A + 2A) = (tan A + tan 2A)/(1−tanA tan 2A)
⇒ tan 3A [1 -tan A tan 2A] =tanA + tan2A
⇒ tan 3 A – tan A tan 2A tan 3A = tan A + tan 2A
⇒ tan 3 A – tan A – tan 2A = tan A tan 2A tan 3 A

Que-25: tan 75° – tan 30° – tan 75° tan 30° = 1

Sol: tan 75 – tan 30 – tan75 tan 30 = 1
can also be written as:
tan 75 – tan 30 = 1 + tan75 tan 30 or
tan 75 – tan 30/(1 + tan75 tan 30) = 1
= tan(75-30)
= tan(45) = 1
LHS = RHS = 1.

Que-26: cos 2θ cos 2Φ + din² (θ – Φ) – sin² (θ + Φ) = cos (2θ + 2Φ).

Sol: L.H.S = cos 2θ cos 2Φ + sin² (θ – Φ) – sin² (θ + Φ)
= cos 2θ cos 2Φ) + sin (θ – Φ + θ + Φ) sin (θ – Φ – θ – Φ) [∵ sin² A – sin² B = sin (A + B) sin (A – B)]
= cos 2θ cos 2Φ + sin 2θ sin (- 2Φ) = cos 2θ cos 2Φ – sin 2θ sin 2Φ
= cos (2θ + 2Φ) = R.H.S

Que-27: If sin (θ + α) = cos (θ + α), prove that tan θ = (1−tanα)/(1+tanα).

Sol: sin (θ + α) = cos (θ + α)
⇒ tan (θ + α) = 1
⇒ θ + α = π/4
⇒ θ = (π/4) – α
⇒ tan θ = tan tan((π/4)−α)
= {tan(π/4)−tanα}/{1+tan(π/4) tanα}
⇒ tanθ = (1−tanα)/(1+tanα)

Que-28: Given that A = B + C, prove that tan A – tan B – tan C = tan A tan B tan C.

Sol: Given A = B + C ⇒ tan A = tan (B + C) = (tan B + tan C)/{1−tan B tan C}
⇒ tan A [1 – tan B tan C] = tan B + tan C
⇒ tan A – tan A tan B tan C = tan B + tan C
⇒ tan A – tan B – tan C = tan A tan B tan C

Que-29: If A + B = 45°, show that tan A + tan B + tan A tan B = 1.
Hence, or otherwise, express tan 22°30′ in surd form.

Sol: Given A + B = 45° + B) = tan 45° = 1 ⇒ ; — = 1
⇒ tan A + tan B = 1 – tan A tan B ⇒ tan A + tan B + tan A tan B = 1
putting A = B = 22° 30′ in eqn. (1); we have
2 tan 22° 30′ + tan2 22° 30′ = 1 ⇒ tan² θ + 2 tan θ – 1 = 0 ; where θ = 22° 30′
∴ tan θ = {−2±√(4+4)}/2
= {−2±2√2}/2
= −1±√2
since 22° 30′ lies in first quadrant
∴ tan 22° 30′ > 0
Thus tan θ = tan (22° 30′) = √2 – 1

Que-30: (i) Use the expansion of tan (A – B) to find tan 15° without the use of tables, leaving your answer in surd form with an integral denominator.
(ii) Prove that 2tanA/{1+tan²A} = sin 2A.

Sol: (i) tan 15° = tan (45°-30°) = (tan 45°  – tan 30°)/{1-tan 45° tan 30°}
= tan 15° = {1-(1/√3)}/{1+(1/√3)}
= {(√3-1)/(√3+1)} × {(√3-1)/(√3-1)}
= {3+1-2√3}/(3-1)
= tan 15° = {4-2√3}/2
= 2 – √3.

(ii) 2tan A/ (1 + (tan A)²)
=> [2* sin A / cos A]/ [ 1 + (sin A)² / (cos A)²]
=> [2* sin A / cos A]/ [ ((cos A)² + (sin A)²) / (cos A)²]
=> [2 sin A* (cos A)² / cos A]/ [ (cos A)² + (sin A)²]
=> [2 sin A * cos A] / 1
=> sin 2A

Que-31: If A + B = 225°, prove that tan A + tan B = 1 – tan A tan B.

Sol: Given A + B = 225°
⇒ tan (A + B) = tan 225°
⇒ (tan A + tan B)/{1−tan A tan B}
= tan (180° + 45°)
= tan 45° =1
⇒ tan A + tan B = 1 – tan A tan B

–: End Compound and Multiple Angles Class 11 OP Malhotra Exe-5A ISC Math Ch-5 Solutions :–

Return to :- OP Malhotra ISC Class-11 S Chand Publication Maths Solutions

Thanks

Please share with your friends