Compound and Multiple Angles Class 11 OP Malhotra Exe-5C ISC Maths Solutions Ch-5 Solutions. In this article you would learn about Double-Angle Formulae. Step by step solutions of latest textbook has been given as latest syllabus. Visit official Website CISCE for detail information about ISC Board Class-11 Mathematics.

Compound and Multiple Angles Class 11 OP Malhotra Exe-5C ISC Maths Solutions Ch-5
| Board | ISC |
| Publications | S Chand |
| Subject | Maths |
| Class | 11th |
| Chapter-5 | Compound and Multiple Angles |
| Writer | OP Malhotra |
| Exe-5(C) | Double-Angle Formulae. |
Exercise- 5C
Compound and Multiple Angles Class 11 OP Malhotra Exe-5C Solution.
Que-1: Evaluate:
(i) 2 sin 15° cos 15°
(ii) 1 – 2 sin² 22.5°
(iii) 2 cos² 157.5° – 1
(iv) cos² (π/2) – sin² (π/2)
(v) (1/2) – sin² (7π/12)
(vi) cos (π/8) sin (π/8)
(vii) 1/2
(viii) 8 cos³ (π/9) – 6 cos (π/9)
Sol: (i) 2 sin 15° cos 15° = sin (2 x 15°)
= sin 30° = 1/2
(ii) 1 – 2 sin² 22.5° = cos (2 x 22.5°)
= cos 45° = 1/√2
(iii) 2 cos² 157.5° – 1 = cos (2 x 157.5°)
= cos (315°)
= cos (360° – 45°) [∵ cos 2θ = 2 cos² θ – 1]
= cos 45° = 1/√2
(iv) cos² (π/12) – sin² (π/12)
= cos (2 x (π/12))
= cos (π/6)
= √3/2 [∵ cos² θ – sin² θ = cos 2θ]
(v) (1/2) – sin² (7π/12)
= (1/2)[1 – sin² (7π/6)]
= (1/2) cos [2×(7π/6)]
= (1/2) cos (7π/6)
= (1/2) cos (π+(π/6))
= (-1/2) cos (π/6)
= (-1/2) × (√3/2)
= -√3/4.
(vi) cos (π/8) sin (π/8)
= (1/2) [2 sin (π/8) cos (π/8)]
= (1/2) sin [2×(π/8)]
= (1/2) sin (π/4)
= 1/2√2
(vii) [2 tan {22*(1/2)}°] / [1-tan²{22*(1/2)}°]
= tan {22*(1/2)}°
= tan 45° = 1.
(viii) 8 cos³ (π/9) – 6 cos (π/9)
= 2[4cos³ (π/9) – 3 cos (π/9)]
= 2 cos (3×(π/9))
= 2 cos (π/9)
= 2 × (1/2)
= 1.
Que-2: Find the values of sin 2θ, cos 2θ, and tan 2θ, given :
(i) sin θ = 3/5, θ in Quadrant I.
(ii) sin θ = 3/5, θ in Quadrant II.
(iii) sin θ = – 1/2, θ in Quadrant IV.
(iv) tan θ = – 1/5, θ in Quadrant II.
Sol: (i) Given sin θ = 3/5
since θ lies in first quadrant ∴ cos θ > 0
∴ θ = √(1-sin²θ) = √{1-(9/25)²} = 4/5
∴ sin 2θ = 2 sin θ cos θ = 2 x (3/5) x (4/5) = 24/25
Thus, cos 2θ = 1 – 2 sin² θ
= 1 – 2(3/5)² = 1 – 2 x (9/25) = 7/25
and tan 2θ = sin2θ/cos2θ
= (24/25)/(7/25) = 24/7.
(ii) Given sin θ = 3/5
since θ lies in 2nd quadrant ∴ cos θ < 0
cosθ = √(1-sin²θ)
= -√{1-(9/25)} = 4/5
sin 2θ = 2 sin θ cos θ
= 2×(3/5)×(-4/5) = -24/25
Thus cos 2θ = 1 – sin²θ
= 1 – 2(3/5)²
= 1 – (18/25) = 7/25
and tan 2θ = (sin 2θ)/(cos 2θ)
= (-24/25) × (25/7)
= -24/7
(iii) given sin θ = –1/2 since θ lies in IVth quadrant ∴ cos θ > 0
cos θ = √(1-sin²θ)
= √(1-(-1/2)²)
= √(1-(1/4)) = √3/2
sin 2θ = 2 sin θ cos θ
= 2 × (-1/2) × (√3/2) = -√3/2
Thus, cos 2θ = 1 – sin²θ
= 1 – 2(-1/2)²
= 1 – 2×(1/4) = 1/2
tan 2θ = (sin 2θ)/(cos 2θ)
= (-√3/2)/(1/2)
= -√3
(iv) Given tan θ = – 1/5
since θ lies in 2nd quadrant,
sin θ > 0 and cos θ < 0
secθ = -√(1+tan²θ)
= -√(1+(-1/5)²)
= -√(1+(1/25))
= -√(26)/5
cos θ = -5/√(26)
sin θ = √(1-cos²θ)
= √(1-(25/26))
= 1/√(26)
sin 2θ = 2sin θ cos θ
= 2 × (1/√(26)) × (-5/√(26))
= -10/26 = -5/13
Thus, cos 2θ = 1 – 2sin²θ
= [1-2{1/√26}]²
= 1 – (2/26) = 12/13
and tan 2θ = (sin 2θ)/(cos 2θ)
= (-5/13)/(12/13)
= -5/12.
Que-3: ABC is an acute-angled triangle inscribed in a circle of radius 5 cm and centre O. The sine of angle A is equal to 3/5. Calculate without using tables :
(i) the length of BC
(ii) sin OBC
(iii) sin BOC
(iv) cos BOC.
Sol: (i) Since ∠BOC = 2 x ∠BAC = 2A
[We know that angle subtended by an arc at the centre is twice the angle subtended by it on circumference of a circle]
Since AD ⊥ BC ∴ OD ⊥ BC
Thus, ∠BOD = ∠COD = A
In ∆BOD, (BD/OB) = sin A
⇒ BD = 5 sin A
We know that ⊥ drawn from centre of circle bisects the chord.
∴ BC = 2BD = 2 x 5 sin A
⇒ BC = 10 sin A = 10 x (3/5) = 6
(ii) From figure ; B = 90° – A
∴ sin ∠OBC = sin (90° – A) = cos A
= + 1−√(1-sin²A)
Thus sin ∠BOC = √(1-sin²A)
= √(1-(3/5)²) = √(1-(9/25)) = 4/5
(iii) sin ∠BOC = sin 2A = 2 sin A cos A
= 2 x (3/5) x (4/5) = 24/25.
(iv) cos BOC = cos 2A = 1 – 2 sin² A
= 1 – 2 x (3/5)²
= 1 – 2 x (9/25)
= 7/25
Que-4: Derive functions of 120° from functions of 60° and check by using relations between functions of supplementary angles.
Sol: Given, θ = 60°.
Now, we have to derive functions of 120 degrees(2 * 60 = 2θ)
(i) sin 2θ = 2 sinθ cosθ
= 2 sin60 cos60
= 2 (√3/2) (1/2)
= √3/2
Verification:
Supplementary angle = 180°.
sin 120 = sin(180 – 60)
= sin 60 {sin (180 – θ) = sin θ}
= √3/2
∴ Hence, verified!
(ii) cos 2θ = 1 – 2sin²θ
= 1 – 2(3/4)
= -1/2
Verification:
cos 120 = cos(180 – 60)
= -cos 60 {cos(180 – θ) = -cosθ}
= -1/2
∴Hence, verified!
(iii) tan 2θ = sin 2θ/cos 2θ
= (√3/2) * (-2)
= -√3
Verification:
tan 120 = tan(180 – 60)
= tan 60 {tan(180 – θ) = -tanθ}
= -√3
∴ Hence, verified!
(iv) cot 2θ = cos 2θ/sin 2θ
= (-1/2) * (2/√3)
= -1/√3
Verification:
cot 120 = cot(180 – 60)
= -cot 60 {cot (180 – 60} = -cot 60}
= -1/√3
∴Hence, verified!
(v) sec 2θ = (1/cos2θ)
= (1/-1/2)
= -2
Verification:
sec 120 = sec(180 – 60)
= -sec 60 {sec (180 – θ) = -secθ}
= -2.
Hence, verified!
(vi) cosec 2θ = (1/sin 2θ)
= (1/√3/2)
= 2/√3
Verification:
cosec 120 = cosec (180 – 60)
= cosec 60 {cosec(180 – θ) = cosecθ}
= 2/√3
∴ Hence, verified.
Que-5: If sin θ = a and sin 2θ = b, find an expression for cos 6 in terms of a and b. hence find a relation between a and b not involving θ.
Sol: Given sin θ = a and sin 2θ = b …(1)
⇒ b = 2 sin θ cos θ = 2 x a cos θ [using (1)]
⇒ cos θ = b/2a … (2)
squaring and adding eqn. (1) and (2); we have
sin² θ + cos² θ = a² + (b/2a)² = a² + b²/4a²
⇒ 1 = a² + (b²/4a²)
⇒ 4a^4 + b² = 4a²
which is the required relation between a and b.
Que-6: (i) Given that tan A = (1/5), find the values of tan 2A, tan 4A and tan (45° – 4A).
(ii) If A is an obtuse angle whose sine is (5/13) and B is an acute angle whose tangent is (3/4), without using tables find the values of
(a) sin 2B, (b) tan (A – B).
Sol: (i) tan 2A = 2 tan A / ( 1- tan² A )
= 2(1/5) / 1 – (1/25)
= (2/5) / (24/25)
= ( 2 × 25 ) / ( 24 × 5 )
= 5 / 12
tan 4A = (2tan 2A) / (1-2tan² 2A)
= 2(5/12) / (1 – 25/144)
= (5/6) / (119/144)
= 120/119
tan (45 – 4A) = (tan 45 – tan 4A) / (1 + tan 45 × tan 4A)
= (1 – 120/119) / (1 + 1 × 120/119)
= (-1/119) / (239/119)
= -1 / 239
(ii) cos²A + sin²A = 1
Substituting sin A = 5/13 :
cos²A + (5/13)² = 1
Calculating (5/13)²:
cos²A + (25/169) = 1
Now, subtract 25/169 from 1:
cos²A = 1 − (25/169)
= (169−25)/169
= 144/169
Taking the square root:
cos A = −√(144/169)
= −12/13
(a) sin 2B = 2tanB / (1+tan2B)
Substituting tanB = 3/4 :
sin2B = {2⋅(3/4)}/{1+(3/4)²}
Calculating (3/4)² :
sin2B = (6/4)/{1+(9/16)}
= (6/4)/{(16+9)/16} = (6/4)/{25/16}
Now, multiply by the reciprocal:
sin2B = (6/4) ⋅ (16/25)
= 96/100
= 24/25
(b) tanA = sinA/cosA = (5/13)/(−12/13)
= −5/12
tan(A−B) = (tanA−tanB)/{1+tanA tanB}
Substituting tanA = −5/12 and tanB = 3/4 :
tan(A−B) = {(−5/12)−(3/4)}/{1+(−5/12)(3/4)}
Finding a common denominator for the numerator:
(−5/12) − (3/4)
= (−5/12) − (9/12)
= −14/12 = −7/6
Now calculating the denominator:
1 + (−5/12) (3/4)
= 1 − (15/48)
= (48−15)/48 = 33/48
Now substituting back into the tangent formula:
tan(A−B) = (−7/6)/(33/48)
= (−7/6) ⋅ (48/33)
= −56/33
Que-7: Express
(i) cos 6α in terms of functions of 5α ;
(ii) sin 10 in terms of functions of 5θ ;
(iii) tan 8α in terms of tan 4α;
(iv) cos 2θ in terms of cos 4θ ;
(v) tan 4Φ in terms of cos 8Φ;
(vi) sin 5θ/2 in terms of cos 5θ ;
(vii) cos 20θ in terms of sin 5θ.
Sol: (i) cos 6α = cos (3×2α)
= 2 cos² 3α – 1
(ii) sin 10θ = sin (2×5θ)
= 2 sin 5θ cos 5θ
(iii) tan 8α = tan (2×4α)
= (2tan 4α)/{1-tan² 4α}
(iv) cos² 2θ = (1+ cos 4θ)/2
= cos 2θ = ±√{(1+cos 4θ)/2}
(v) tan² 4Φ = (sin² 4Φ)/(cos² 4Φ)
= (1-cos 8Φ)/(1+cos 8Φ)
= tan 4Φ = √{(1-cos 8Φ)/(1+cos 8Φ)}
(vi) sin 5θ/2
We know that,
sin² θ = (1-cos 2θ)/2
= sin² (5θ/2)
= {1-cos (2×(5θ/2))}/2
= (1-cos 5θ)/2
(vii) cos 20θ = cos (2×10θ)
= 1 – 2sin² 10θ
= 1 – 2[sin(2×5θ)]²
= 1 – 2[2sin 5θ cos 5θ]²
= 1 – 8sin² 5θ (1-sin² 5θ)
= 1 – 8sin² 5θ + 8 sin^4 5θ.
Que-8: Using the half angle formulas, find the exact value of (i) sin² 15° (ii) sin² 292 *(1/2)
Sol: (i) sin² 15° = {1-cos(2×15°)}/2
= (1-cos 30°)/2
sin 15° = √{(1-cos 30°)/2}
sin 15° = √{(1-(√3/2))/2}
= √{2-√3}/2
(ii) sin² 292 *(1/2)
= [1-cos {2×292 *(1/2)}]
= {1-cos(585°)}/2
= {1-cos (360°+225°)}/2
= {1-cos 225°}/2
= {1-cos (180°+45°)}/2

Que-9: In the triangle ABC, in which C is the right angle, prove that:
sin 2A = 2ab/c², cos 2A = (b²–a²)/c²,
sin A/2 = √{(c-b)/2c}, cos A/2 = √{(c+b)/2c}.
Sol: From right angled ∆ACB, we have
sin A = BC/AB = a/c and
cos A = AC/AB = b/c
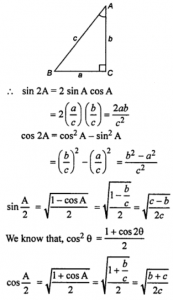
Que-10: If cos α = (3/5), cos ß = (4/5), find the value of cos (α-ß)/2, assuming α and ß to be acute angles.
Sol: cos α = (3/5), cos ß = (4/5)
since α, ß are acute angles
∴ sin α, sin ß > 0
sin α = √(1-cos²α)
= √{1-(9/25)} = 4/5
and sin ß = √(1-cos²ß)
= √{1-(16/25)} = 3/5
cos² θ = (1+cos 2θ)/2
cos² {(α-ß)/2} = {1+cos (α-ß)}/2
= {1+cos α cos ß + sin α sin ß}/2
= {1+ (3/5) (4/5) + (4/5) (3/5)}/2
= {1+(24/25)}/2
= 49/50
Since α, ß are acute angles
(α-ß)/2 be also acute angles
cos (α-ß)/2 > 0
= cos (α-ß)/2
= √(49/50)
= 7√2/(5√2×√2)
= 7√2/10.
Que-11: Given that cos (A/2) = (12/13), calculate without the use of tables, the values of sin A, cos A and tan A.
Sol: Given : cos (A/2) = (12/13)
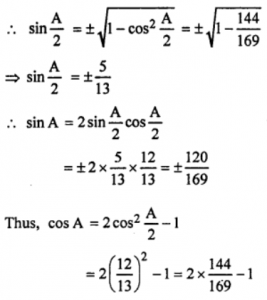
= (288-169)/169
cos A = 119/169
and tan A = sin A/ cos A
= (120/169) / (119/169)
= 120/119
Que-12: Given that tan x = 12/5, cos y = -3/5, and the angles x and y are in the same quadrants, calculate without the use of tables the value of
(i) sin(x + y).
(ii) cos y/2
Sol: tanx = 12/5 and cosy = -3/5
tan is positive but cosine is negative, it is possible only when x and y are located in 3rd quadrant.
so, tanx = 12/5 ⇒sinx = -12/13,cosx = -5/13
[in 3rd quadrant, sine and cosine are negative]
cosy = -3/5 ⇒siny = -4/5
(i) now sin(x + y) = sinx cosy + cosx siny
= (-12/13) (-3/5) + (-5/13) (-4/5)
= 36/65 + 20/65
= 56/65
(ii) Since y lies in 3rd quadrant
y/2 lies in 2nd quadrant
cos y/2 < 0
cos y/2 = √{(1+cos y)/2}
= √{(1+(-3/5))/2}
= √{(2/5)/2}
= -1/√5.
Que-13: Given tan sin² = sin α cos α, show that cos 2ß = 2 cos² [(π/4 + α)]
Sol: Given sin² ß = sin α cos α
⇒ (1−cos2β)/2 = sin α cos α
⇒ 1 – cos 2ß = 2 sin α cos α
⇒ 1 – cos 2ß = sin 2α
⇒ cos 2ß = 1 – sin 2α …(1)
Also 2 cos²((π/4)+α) = 2[{1+cos2((π/4)+α)}/2] [∵ cos² α = (1+cos2θ)/2 ]
= 1 + cos [(π/2) + 2α] = 1 – sin 2α … (2)
∴ from eqn. (1) and eqn. (2); we have
cos 2ß = 2 cos² ((π/4) + α)
Que-14: Derive formulas for the following in terms of functions of 2θ and then of θ.
(i) sin 4θ, (ii) cos 4θ, (iii) tan 4θ.
Sol: (i) sin 4θ = sin (2 x 2θ) = 2 sin 2θ cos 2θ
= 2 (2 sin θ cos θ) (cos² θ – sin² θ)
= 4 sin θ cos θ (cos² θ – sin² θ)
(ii) cos 4θ = cos (2 x 2θ) = 2 cos² 2θ – 1
= [2 (2 cos² θ – 1)² – 1]
= 2 (4 cos4 θ – 4 cos² θ + 1) – 1
= 8 cos4 θ – 8 cos² θ + 1
(iii) tan 4θ = tan (2 x 2θ) = 2tan2θ/(1−tan² 2θ)
= 2[(2tanθ/(1−tan²θ)] / [1−(2tanθ/(1−tan²θ)²]
= [4tanθ (1−tan²θ)] / [(1−tan²θ)²−4tan²θ]
= [4tanθ (1−tan²θ)] / [tan^4θ − 2tan²θ + 1 − 4tan²θ]
= [4tanθ (1−tan²θ)] / [tan^4θ − 6tan²θ + 1]
Que-15: If sin α = 3/5, find the value of
(i) sin 3α, (ii) cos 3α, (iii) tan 3α.
Sol: We use the formula for sin3θ:
sin3θ = 3sinθ − 4sin³θ
Substituting θ = α :
sin3α = 3sinα − 4sin³α
Now substituting sinα = 3/5 :
sin3α = 3(3/5) − 4(3/5)³
Calculating (3/5)³ :
(3/5)³ = 27/125
(i) sin3α = (9/5) − 4 ⋅ (27/125)
Calculating 4⋅(27/125) :
4⋅(27/125) = (108/125)
Now substituting:
sin3α = (9/5) − (108/125)
Converting 95 to have a common denominator of 125:
(9/5) = (225/125)
Now substituting:
sin3α = (225/125) − (108/125)
= 117/125
(ii) We know that:
cos²θ = 1−sin²θ
Thus:
cos²3α = 1−sin² 3α
Calculating sin² 3α :
sin² 3α = (117/125)² = 13689/15625
Now substituting:
cos² 3α = 1 − (13689/15625)
Converting 1 to have a common denominator:
1 = (15625/15625)
Now substituting :
cos² 3α = (15625−13689)/15625 = 1436/15625
Taking the square root:
cos3α = ±√(1436/15625) = ±√(1436/125)
Calculating √1436:
√1436 = 38 (approximately, since 1436 = 4×359)
Thus:
cos3α = ± 38/125
(iii) Using the formula:
tan3α = sin3α / cos3α
Substituting the values:
1. For cos3α = 38/125 :
tan3α = (117/125) / (38/125) = 117/38
2. For cos3α = −38/125 :
tan3α = (117/125) − (38/125)
= −117/38
Que-16: If 2 cos θ = x + (1/x), prove that 2 cos 3θ = x³ + (1/x³)
Sol: Given : 2 cos θ = x + (1/x)
2cos 3θ = 2 [4cos³ θ – 3cos θ]

= {x + (1/x)}³ – 3{x + (1/x)}
= x³ + (1/x³) + 3x × (1/x) {x+(1/x)} – 3{x+(1/x)}
= x³ + 1/x³
Que-17: Calculate without using tables tan 20° tan 40° tan 80°.
Sol: Given : tan 20° tan 40° tan 80°
= tan 20° tan (60°-20°) tan (60°+20°)

= [3tan 20° – tan³ 20°]/[1-3tan² 20°]
= tan (3×20°) = tan 60°
= √3.
–: End Compound and Multiple Angles Class 11 OP Malhotra Exe-5C ISC Math Ch-5 Solution :–
Return to :- OP Malhotra ISC Class-11 S Chand Publication Maths Solutions
Thanks
Please share with your friends