Compound Interest Class 9 OP Malhotra Exe-2C ICSE Maths Solutions Ch-2 We Provide Step by Step Solutions / Answer of Questions on compound Interest using formula if rate of interest change in successive year OP Malhotra Maths. Visit official Website CISCE for detail information about ICSE Board Class-9 Mathematics.

Compound Interest Class 9 OP Malhotra Exe-2C ICSE Maths Solutions Ch-2
| Board | ICSE |
| Publications | S Chand |
| Subject | Maths |
| Class | 9th |
| Chapter-2 | Compound Interest |
| Writer | OP Malhotra |
| Exe-2C | Using Formula if rate of interest change in successive year |
| Edition | 2025-2026 |
Exercise- 2C
Compound Interest Class 9 OP Malhotra ICSE Maths Solutions Ch-2
Que-1: What amount of money should Mohan invest in a bank in order to get ₹ 1323 in 2 years at 5% compounded annually?
Sol: Amount after 2 years = ₹ 1323
Rate (R) = 5% p.a.
Period = 2 years
Now A = P (1+(R/100))^n
⇒ ₹ 1323 = P (1+(5/100))²
⇒ ₹ 1323 = P (21/20)²
= P = ₹ 1323 x (20/21)²
= 1323 x (20/21) x (20/21) = ₹ 1200
∴ Principal = ₹ 1200
Que-2: Find the sum which amounts to ₹ 1352 in 2 years at 4% compound interest.
Sol: Amount after 2 years = ₹ 1352
Rate (R) = 4% p.a.
Now A = P (1+(R/100))^n
⇒ ₹ 1352 = P (1+(4/100))²
⇒ ₹ 1352 = P x (26/25)²
= P = ₹ 1352 x (25/26)²
= ₹ 1352 x (25/26) x (25/26) = ₹ 1250
∴ Principal = ₹ 1250
Que-3: What principal will amount to ₹ 9768 in two years. If the rates of interest for the successive years are 10% p.a. and 11% p.a. respectively.
Sol: Amount after 2 years = ₹ 9768
Rate of interest for the first year (r1) = 10% p.a.
and for the second year (r2) = 11% p.a.
Now A = P {1+((r1)/100)}{1+(r2)/100)}
⇒ 9768 = P {1+(10/100)}{(1+(11/100)}
⇒ 9768 = P (11/10)(111/100)
∴ P = ₹ 9768 x (10/11) x (100/11) = ₹ 8000
∴ Principal = ₹ 8000
Que-4: On what sum of money does the difference between the simple interest and compound interest in 2 years at 5% per annum is Rs. 15?
Sol: Let principal (P) = ₹ 100
Rate (R) = 5% p.a.
Period in) = 2 years
Difference between S.I. and C.I. = ₹ 15
Now S.I = PRT/100
= (100×5×2)/100 = ₹ 10
and by compound interest
A = P (1+(R/100))^n
⇒ 100 (1+(5/100))²
⇒ 100 x (21/20)²
= ₹ 100 x (21/20) x (21/20) = ₹ 441/4
C.I. = A – P
= (441/4) – 100
= 41/4.
Now difference between S.I. and C.I. = (41)/4) – 10
= ₹ (41−40)/4 = ₹ 14
If difference is ₹ 14, then principal = ₹ 100
If difference is ₹ 1, then principal = ₹ (100×4)/1
and if difference is ₹ 15, then principal
= ₹ (100×4×15)/1 = ₹ 6000
Hence principal = ₹ 6000
Que-5: The difference between simple and compound interest on the same sum of money at 6*(2/3)% for 3 years is ₹ 184. Determine the sum.
Sol: Difference between C.I. and S.I. = ₹ 184
Let principal (Sum) = Rs. 100
Rate (R) = 6*(2/3) % = 20/3 %
Period (n) = 3 years
Simple interest = PRT/100
= (100×20×3)/(100×3)
= ₹ 20
and by compound interest
A = P (1+(R/100))^n
⇒ 100 (1+(20/3×100))³
⇒ 100 x (16/15)³
= ₹ 100 x (16/15) x (16/15)
= ₹ 16384/135
C.I. = A – P
= (16384/135) – 100
(16384-13500)/100
= 2884/135.
Now, difference between C.I. and S.I.
= (2884/135) – 20
= (2884-2700)/135
⇒ 184/135
If difference is ₹ 184/135, then principal = ₹ 100
If difference is ₹ 1 then principal
= (100×135)/184
and if difference is ₹ 184, then principal
= (100×135×184)/184 = ₹ 13500.
Que-6: On what sum of money will the difference between the simple interest and the compound interest for 2 years at 5% per annum be equal to ₹ 50.
Sol: Time is 2 years
Rate is 5% per annum
The difference between simple interest and compound interest is Rs. 50.
S.I = (P × R × T)/100
C.I = P[(1 + r/100)n – 1]
Let sum be Rs. P
Now,
The simple interest for 2 years at 5% per annum is
(P × 5 × 2)/100
⇒ P/10
Now,
The compound interest for 2 years at 5% per annum is
P[(1 + 5/100)2 – 1]
⇒ P[(21/20)2 – 1]
⇒ P[(441/400) – 1]
= 41P/400
So,
The difference between Compound interest and simple interest is
⇒ 41p/400 – P/10 = 50
⇒ 41P – 40P = 50 × 400
OR P = Rs. 20000.
Que-7: Find the rate per cent per annum, if compounded yearly
(i) Principal = ₹ 196, Amount = ₹ 225, time = 2 years
(ii) Principal = ₹ 3136, Compound interest = ₹ 345, Time = 2 years
Sol: (i) Total payment = 225 Rs
Principal = 196 Rs
Time = 2 years
Total due after compounding interesting
Total payment = P (1 + r)^t
225 = 196 (1 + r)^2
225/196 = (1 + r)^2
Taking root on both sides –
15/14 = 1 + r
r = 15/14 – 1, r = 1/14
So 1/14 × 100 %
r = 50/7 %
r = 7*(1/7) %.
(ii) P = Rs. 3136, n = 2 years. Compound interest = Rs. 345
Compound interest = Amount – Principal
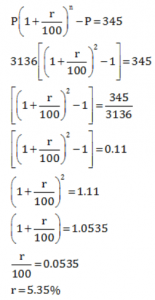
Que-8: Hari purchased Relief Bonds for ^1000, a sum which will fetch him ₹ 2000 after 5 years. Find the rate of interest if the interest is compounded half-yearly.
Sol: Principal (P) = ₹ 1000
Amount (A) = ₹ 2000
Period (n) = 5 years = 10 half years
We know that,
A/P = (1+(R/100))^n
⇒ 2000/1000 = (1+(R/100))^10
⇒ 2/1 = (1+(R/100))^10
1 + (R/100) = 10√2 = 1.072
R/100 = 1.072 – 1.000 = 0.072
R = 0.072 x 100 = 7.2
∴ Rate half-yearly = 7.2%
and rate annually = 7.2 x 2 = 14.4% p.a.
Que-9: ₹ 8000 became ₹ 9261 in a certain interval of time at the rate of 5% per annum C.l. Find the time.
Sol: Principal (P) = ₹ 8000
Amount (A) = ₹ 9261
Rate (R) = 5% p.a.
We know that,
A/P = (1+(R/100))^n
⇒ 9261/8000 = (1+(5/100))^n
⇒ 9261/8000 = (21/20)^n
= (21/20)³ = (21/20)^n
Comparing, we get n = 3
∴ Period = 3 years
Que-10: In how many years will a sum of ₹ 3000 at 20% per year compounded semi-annually become ₹ 3993.
Sol: Principal (P) = ₹ 3000
Amount (A) = ₹ 3993
Rate (R) = 20% p.a. or 10% half-yearly
We know that,
A/P = (1+(R/100)^n
⇒ 3993/3000 = (1+(10/100))^n
= 1331/1000 = (11/10)^n
⇒ (11/10)³ = (11/10)^n
Comparing, we get n = 3
∴ Period = 3 half years or 1*(1/2) years
Que-11: A sum of money put out at compound interest amounts in 2 years to ₹ 578.40 and in 3 years to ₹ 614.55. Find the rate of interest.
Sol: Amount for 3 years = ₹ 614.55
Amount for 2 years = ₹ 578.40
Subtracting,
Interest for 1 year = ₹ 36.15
∴ ₹ 36.15 is interest on ₹ 578.40 for 1 year
∴ Rate = (Simple interest ×100)/(P× Time)
= (36.15×100)/(578.40×1)
= 25/4%
hence 6*(1/4) % p.a.
Que-12: A sum compounded annually becomes 25/16 times of itself in 2 years. Determine the rate of interest per annum?
Sol: Let Principal (P) = ₹ 1
Then Amount (A) = ₹ 2516
Period (n) = 2 years
Let R be the rate of interest per annum, then
A/P = (1+(R/100))^n
25/16 = (1+(R/100))²
⇒ (5/4)² = (1+(R/100))²
Comparing, we get
1 + (R/100) = 5/4
⇒ R/100 = (5/4) − 1 = (5−4)/4 = 1/4
∴ R = (1/4) x 100 = 25
∴ Rate = 25 % p.a.
— : End of Compound Interest Class 9 OP Malhotra Exe-2C ICSE Maths Ch-2 Step by Step Solutions :–
Return to :– OP Malhotra S Chand Solutions for ICSE Class-9 Maths
Thanks
Please Share with Your Friends


