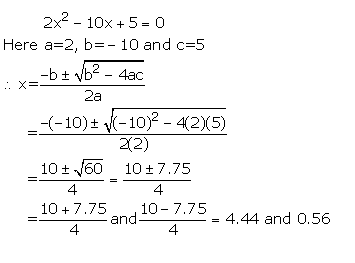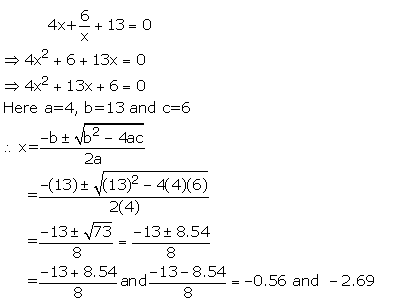Concise Solutions Quadratic Equations Chapter 5 for ICSE Maths Class 10 is available here. All Solution of Concise of Chapter 5 Quadratic Equations in One Variable has been solved according instruction given by council. This is the Solution of Chapter-5 Quadratic Equation in one variable for ICSE Class 10th .ICSE Maths text book of Concise is In series of famous ICSE writer in maths. Concise is most famous among students. With the help of Concise solution student can achieve their goal in 2020 exam of council.
Concise Solutions Quadratic Equations Chapter 5 for ICSE Maths Class 10
The Solution of Concise Mathematics Chapter 5 Quadratic Equations for ICSE Class 10 have been solved by experience teachers from across the globe to help students of class 10th ICSE board exams conducted by the ICSE (Indian Council of Secondary Education) board papering in 2020. Therefore the ICSE Class 10th Maths Solutions of Concise solve problems of exercise and Chapter test related to various topics which are prescribed in most ICSE Maths textbooks.
Chapter- 5 ,Quadratic Equations “Concise Maths Solutions”
Select Topics
Exe 5(D) ,
Exe 5(E) ,
How to Solve Concise Solutions Quadratic Equations
Note:- Before viewing Solutions of Chapter -5 Quadratic Equations of Concise Maths read the Chapter Carefully then solve all example of your text book. The Chapter- 5 Quadratic Equations is main Chapter in ICSE board .
Solutions of Concise Maths Chapter 5 – Quadratic Equations
Exercise- 5(A)
Question 1
Find which of the following equation are quadrants.
(i) (3x – 1)2 = 5(x + 8)
(ii) 5x2 – 8x = -3(7 – 2x)
(iii) (x – 4)(3x + 1) = (3x – 1)(x +2)
(iv) x2 + 5x – 5 = (x – 3)2
(v) 7x3 – 2x2 + 10 = (2x – 5)2
(vi) (x – 1)2 + (x + 2)2 + 3(x +1) = 0
Answer 1
(i)
(3x – 1)2 = 5(x + 8)
⇒ (9x2 – 6x + 1) = 5x + 40
⇒ 9x2 – 11x – 39 =0; which is of the form ax2 + bx + c = 0.
∴ Given equation is a quadratic equation.
(ii)
5x2 – 8x = -3(7 – 2x)
⇒ 5x2 – 8x = 6x – 21
⇒ 5x2 – 14x + 21 =0; which is of the form ax2 + bx + c = 0.
∴ Given equation is a quadratic equation.
(iii)
(x – 4)(3x + 1) = (3x – 1)(x +2)
⇒ 3x2 + x – 12x – 4 = 3x2 + 6x – x – 2
⇒ 16x + 2 =0; which is not of the form ax2 + bx + c = 0.
∴ Given equation is not a quadratic equation.
(iv)
x2 + 5x – 5 = (x – 3)2
⇒ x2 + 5x – 5 = x2 – 6x + 9
⇒ 11x – 14 =0; which is not of the form ax2 + bx + c = 0.
∴ Given equation is not a quadratic equation.
(v)
7x3 – 2x2 + 10 = (2x – 5)2
⇒ 7x3 – 2x2 + 10 = 4x2 – 20x + 25
⇒ 7x3 – 6x2 + 20x – 15 = 0; which is not of the form ax2 + bx + c = 0.
∴ Given equation is not a quadratic equation.
(vi)
(x – 1)2 + (x + 2)2 + 3(x +1) = 0
⇒ x2 – 2x + 1 + x2 + 4x + 4 + 3x + 3 = 0
⇒ 2x2 + 5x + 8 = 0; which is of the form ax2 + bx + c = 0.
∴ Given equation is a quadratic equation.
Question 2
(i) Is x = 5 a solution of the quadratic equation x2 – 2x – 15 = 0?
(ii) Is x = -3 a solution of the quadratic equation 2x2 – 7x + 9 = 0?
Answer 2
(i)
x2 – 2x – 15 = 0
For x = 5 to be solution of the given quadratic equation it should satisfy the equation.
So, substituting x = 5 in the given equation, we get
L.H.S = (5)2 – 2(5) – 15
= 25 – 10 – 15
and = 0
hence = R.H.S
Hence, x = 5 is a solution of the quadratic equation x2 – 2x – 15 = 0.
(ii)
2x2 – 7x + 9 = 0
For x = -3 to be solution of the given quadratic equation it should satisfy the equation
So, substituting x = 5 in the given equation, we get
L.H.S=2(-3)2 – 7(-3) + 9
= 18 + 21 + 9
= 48
≠ R.H.S
Hence, x = -3 is not a solution of the quadratic equation 2x2 – 7x + 9 = 0.
Question 3
If 
is a solution of equation 3x2 + mx + 2 = 0, find the value of m.
Answer 3
For x = √2/√3 to be solution of the given quadratic equation it should satisfy the equation
So, substituting x = √2/√3 in the given equation, we get
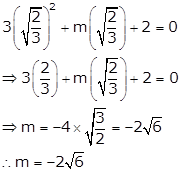
Question 4
and 1 are the solutions of equation mx2 + nx + 6 = 0. Find the values of m and n.
Answer 4
Question 5
If 3 and -3 are the solutions of equation ax2 + bx – 9 = 0. Find the values of a and b.
Answer 5
Quadratic Equations Chapter- 5 Concise Solutions Exercise – 5(B) for ICSE Maths Class 10
Exercise – 5(B)
Question 1
Without solving, comment upon the nature of roots of each of the following equations :
(i)7x2 – 9x +2 =0 (ii)6x2 – 13x +4 =0
(iii)25x2 – 10x +1=0 (iv)
(v)x2 – ax – b2 =0 (vi)2x2 +8x +9=0
Answer 1
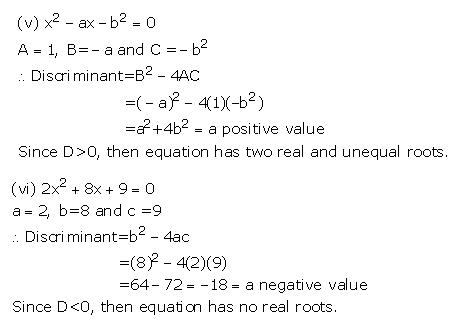
Question 2
Find the value of p, if the following quadratic equation has equal roots : 4x2 – (p – 2)x + 1 = 0
Answer 2
Question 3
Find the value of ‘p’, if the following quadratic equations have equal roots :
x2 + (p – 3)x + p = 0
Answer 3
x2 + (p – 3)x + p = 0
Here, a = 1, b = (p – 3), c = p
Since, the roots are equal,
⇒ b2– 4ac = 0
⇒ (p – 3)2– 4(1)(p) = 0
⇒p2 + 9 – 6p – 4p = 0
⇒ p2– 10p + 9 = 0
⇒p2-9p – p + 9 = 0
⇒p(p – 9) – 1(p – 9) = 0
⇒ (p -9)(p – 1) = 0
⇒ p – 9 = 0 or p – 1 = 0
⇒ p = 9 or p = 1
Question 4
The equation 3x2 – 12x + (n – 5)=0 has equal roots. Find the value of n.
Answer 4
Question 5
Find the value of m, if the following equation has equal roots : (m – 2)x2 – (5+m)x +16 =0
Answer 5
Exercise-5(C) ,Chapter 5 – Quadratic Equations Concise Maths Solutions for ICSE Maths Class 10th
Exercise 5(C)
Solve equation, number 1 to 20 given below using factorization method:
Question 1
Solve : x²-10x-24 = 0
Answer 1
Question 2
Solve : 
Answer 2
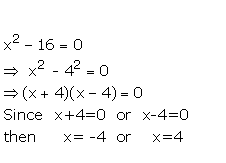
Question 3
Solve : 
Answer 3
Question 4
Solve : x(x-5)= 24
Answer 4
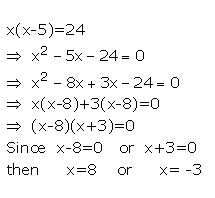
Question 5
Solve : 
Answer 5
Question 6
Solve : 
Answer 6
Question 7
Solve : 
Answer 7
Question 8
Solve : 
Answer 8
Question 9
Solve : 
Answer 9
Question 10
Solve : 
Answer 10
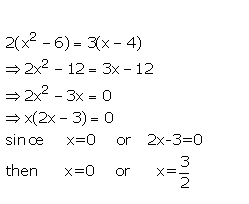
Question 11
Solve : 
Answer 11
Question 12
Solve : 
Answer 12
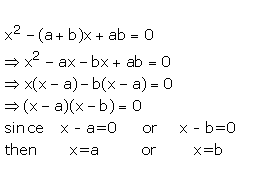
Question 13
Solve : 
Answer 13
Question 14
Solve : 
Answer 14
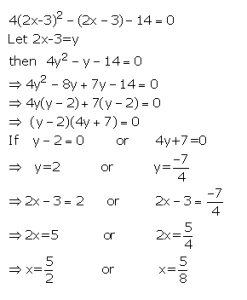
Question 15
Solve : 
Answer 15
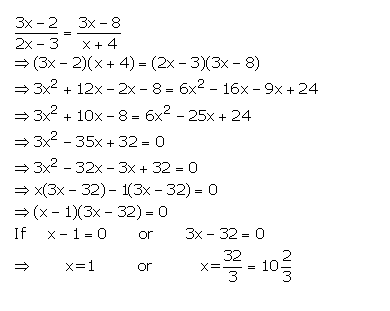
Question 16
2x2 – 9x + 10 = 0, When
(i) x∈ N
(ii) x∈ Q
Answer 16
Question 17
Solve : 
Answer 17
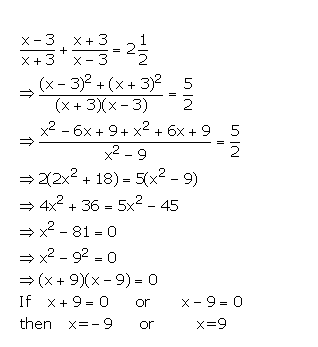
Question 18
Solve : 
Answer 18
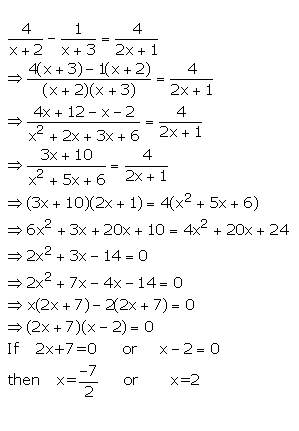
Question 19
Solve : 
Answer 19
Question 20
Solve : 
Answer 20
Question 21
Find the quadratic equation, whose solution set is :
(i) {3, 5} (ii) {-2, 3}
Answer 21
Question 22
Answer 22
Question 23
Answer 23
Question 24
Find the value of x, if a + 1=0 and x2 + ax – 6 =0.
Answer 24
If a+1=0, then a = -1
Put this value in the given equation x2 + ax – 6 =0
Question 25
Find the value of x, if a + 7=0; b + 10=0 and 12x2 = ax – b.
Answer 25
If a + 7 =0, then a = -7
and b + 10 =0, then b = – 10
Put these values of a and b in the given equation
Question 26
Use the substitution y= 2x +3 to solve for x, if 4(2x+3)2 – (2x+3) – 14 =0.
Answer 26
4(2x+3)2 – (2x+3) – 14 =0
Put 2x+3 = y
Question 27
Without solving the quadratic equation 6x2 – x – 2=0, find whether 
is a solution of this equation or not.
Answer 27
Consider the equation, 6x2 – x – 2=0
Put in L.H.S.
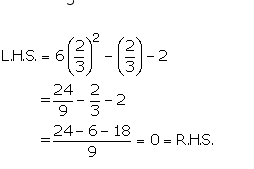
Since L.H.S.= R.H.S., then is a solution of the given equation.
Question 28
Determine whether x = -1 is a root of the equation x2 – 3x +2=0
or not.
Answer 28
x2 – 3x +2=0
Put x = -1 in L.H.S.
L.H.S. = (-1)2 – 3(-1) +2
= 1 +3 +2=6 ≠R.H.S.
Then x = -1 is not the solution of the given equation.
Question 29
If x = 2/3is a solution of the quadratic equation 7x2+mx – 3=0;
Find the value of m.
Answer 29
7x2+mx – 3=0
Given x =2/3 is the solution of the given equation.
Put given value of x in the given equation
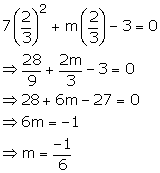
Question 30
If x = -3 and x = 2/3 are solutions of quadratic equation mx2 + 7x + n = 0, find the values of m and n.
Answer 30
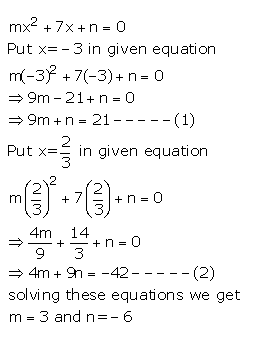
Question 31
If quadratic equation x2 – (m + 1) x + 6=0 has one root as x =3;
find the value of m and the root of the equation.
Answer 31
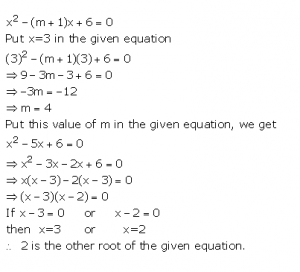
Question 32
Given that 2 is a root of the equation 3x2 – p(x + 1) = 0 and that the equation px2 – qx + 9 = 0 has equal roots, find the values of p and q.
Answer 32
Question 33
Answer 33
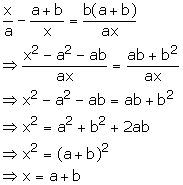
or x = -(a + b)
Question 34
Answer 34
Question 35
If -1 and 3 are the roots of x2+px+q=0
then find the values of p and q
Answer 35
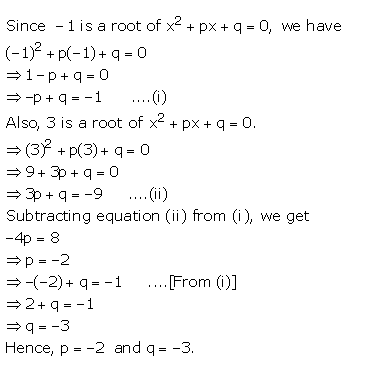
ICSE Concise Solutions Quadratic Equations Exercise – 5(D) Chapter-5
Question 1
Solve each of the following equations using the formula :
(i)x2 – 6x =27 (ii)x2 – 10x +21=0
(iii)x2 +6x – 10 =0 (iv)x2 +2x – 6=0
(v)3x2+ 2x – 1=0 (vi)2x2 + 7x +5 =0
(vii) 
(viii) 
(ix) 
(x) 
(xi) 
(xii) 
(xiii) 
(xiv)
Answer 1
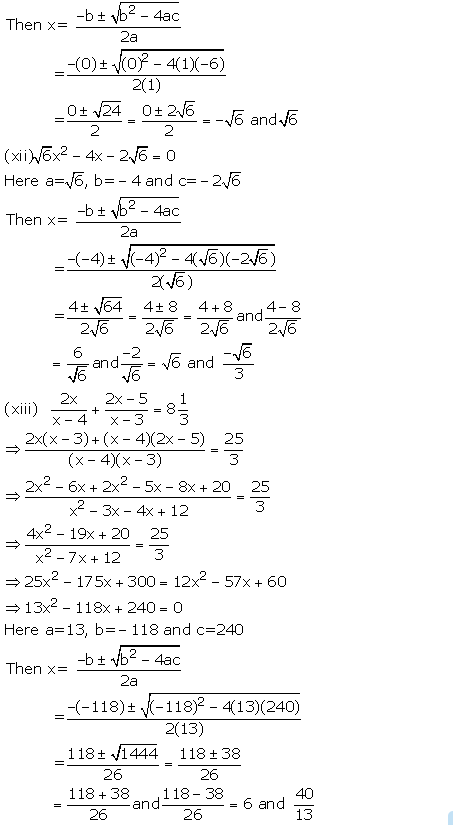
Question 2
Solve each of the following equations for x and give, in each case, your answer correct to one decimal place :
(i)x2 – 8x+5=0
(ii)5x2 +10x – 3 =0
Answer 2
Question 3
Solve each of the following equations for x and give, in each case, your answer correct to two decimal places :
(i)2x2 – 10x +5=0
(ii)
(iii) x2 – 3x – 9 =0
(iv) x2 – 5x – 10 = 0
Answer 3
(i)
(ii)
(iii)
(iv)
Question 4
Solve each of the following equations for x and give, in each case, your answer correct to 3 decimal places :
(i)3x2 – 12x – 1 =0
(ii)x2 – 16 x +6= 0
(iii)2x2 + 11x + 4= 0
Answer 4
Question 5
Solve:
(i)x4 – 2x2 – 3 =0
(ii)x4 – 10x2 +9 =0
Answer 5
Question 6
Solve :
(i)(x2 – x)2 + 5(x2 – x)+ 4=0
(ii)(x2 – 3x)2 – 16(x2 – 3x) – 36 =0
Answer 6
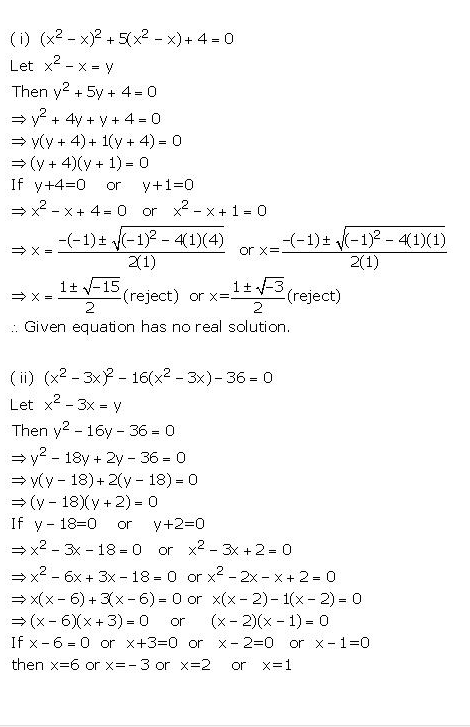
Question 7
Solve :
(i)
(ii)
(iii)
Answer 7
Question 8
Solve the equation . 2x- 1/x= 7. Write your answer correct to two decimal places.
Answer 8
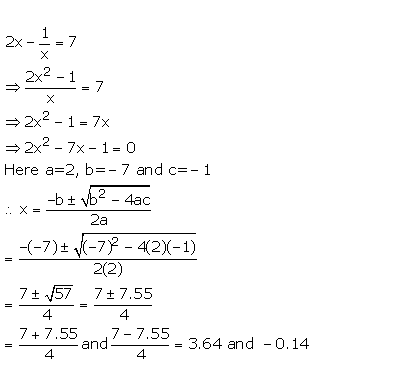
Question 9
Solve the following equation and give your answer correct to 3 significant figures:
Answer 9
Consider the given equation:
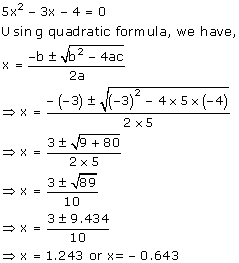
Question 10
Solve for x using the quadratic formula. Write your answer correct to two significant figures.
(x – 1)2 – 3x + 4 = 0
Answer 10
Question 11
Solve the quadratic equation x2 – 3(x + 3)=0 ; Give your answer correct to two significant figures.
Answer 11
x2 – 3(x + 3)=0
Concise Solution Quadratic Equations Chapter -5 Exercise 5(E)
Exercise – 5(E)
Question 1
Solve:
Answer 1
Question 2
Solve: (2x+3)2=81
Answer 2
Question 3
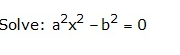
Answer 3
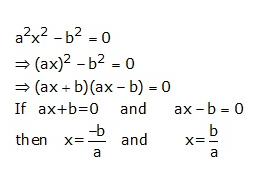
Question 4
Answer 4
Question 5
Answer 5
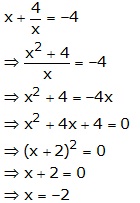
Question 6
Answer 6
Question 7
Answer 7
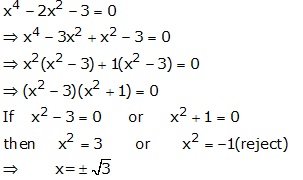
Question 8
Answer 8
Question 9
Answer 9
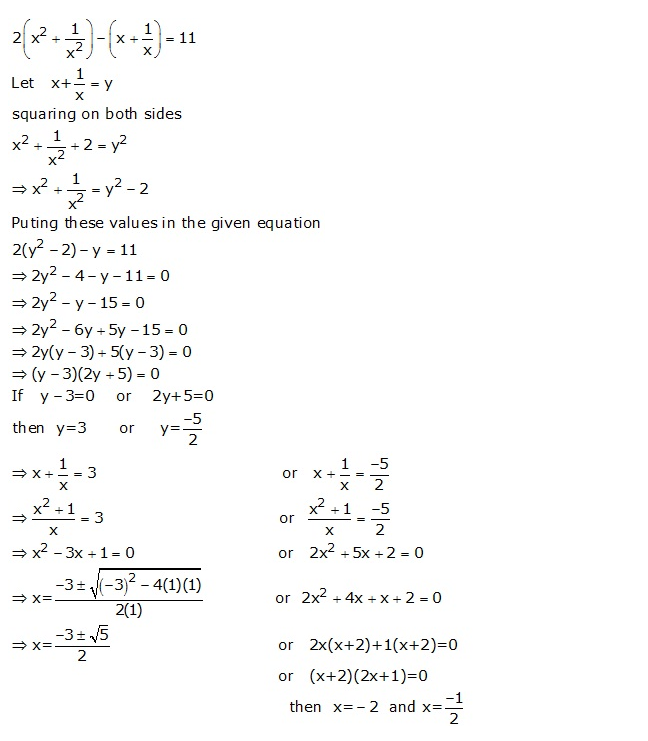
Question 10
Answer 10
Question 11
Answer 11
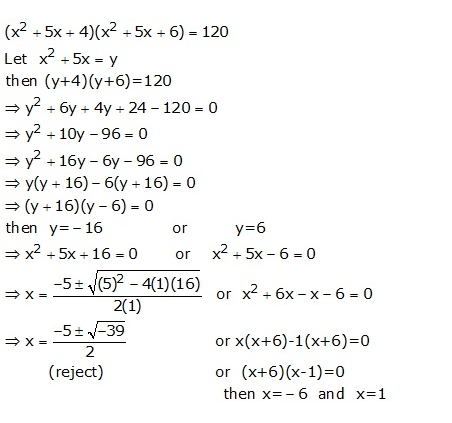
Question 12
Solve each of the following equations, giving answer upto two decimal places.(i)x2 – 5x -10=0(ii) 3x2 – x – 7 =0
Answer 12
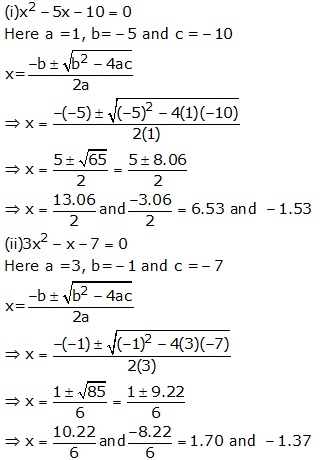
Question 13
Answer 13
Question 14
Solve :
(i)x2 – 11x – 12 =0; when x ∈N
(ii)x2 – 4x – 12 =0; when x∈ I
(iii)2x2 – 9x + 10 =0; when x∈Q
Answer 14
Question 15
Answer 15
Question 16
Answer 16
Question 17
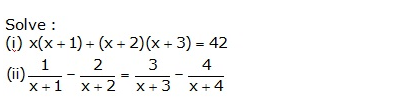
Answer 17
Question 18
Answer 18
Question 19
Answer 19
Question 20
Without solving the following quadratic equation, find the value of ‘m’ for which the given equation has real and equal roots.
Answer 20
Consider the given equation:
Chapter 5 – Quadratic Equations Exercise -5(F) Concise Solutions for ICSE Maths Class 10th
Exercise -5 (F)
Question 1
Solve :
(i) (x+5)(x-5)=24
(ii) 
(iii)
Answer 1
(i)
(ii)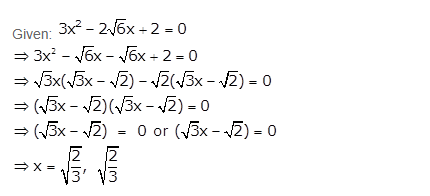
(iii)
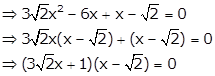
Question 2
One root of the quadratic equation 
is 
. Find the value of m. Also, find the other root of the equation
Answer 2
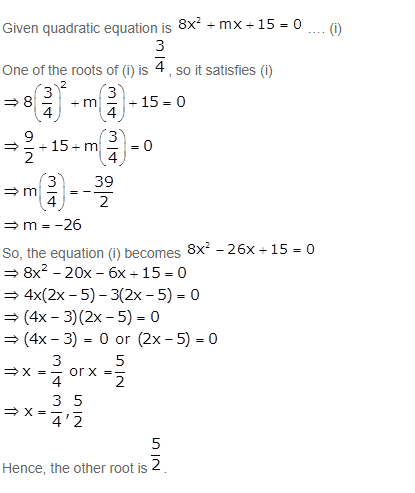
Question 3
One root of the quadratic equation 
is -3, find its other root.
Answer 3
Question 4
If 
and 
;find the values of x.
Answer 4
Question 5
update Soon
Answer 5
Question 6
If m and n are roots of the equation 
where x ≠ 0 and x ≠ 2; find m × n.
Answer 6
Given quadratic equation is 
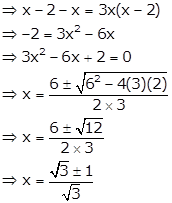
Since, m and n are roots of the equation, we have
and 
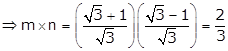
Hence,
Question 7
Solve, using formula :
Answer 7
Given quadratic equation is 
Using quadratic formula,
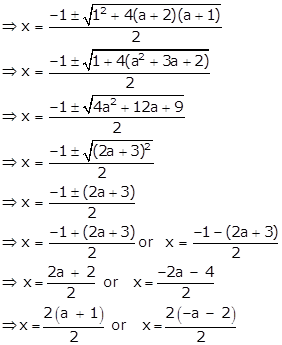
⇒ x = a + 1 or x = -a – 2 = -(a + 2)
Question 8
Solve the quadratic equation 
(i) When 
(integers)
(ii) When 
(rational numbers)
Answer 8
Question 9
Find the value of m for which the equation 
has real and equal roots.
Answer 9
Question 10
Find the values of m for which equation 
has equal roots. Also, find the roots of the given equation.
Answer 10
Question 11
Find the value of k for which equation
has real roots.
Answer 11
Question 12
Find, using quadratic formula, the roots of the following quadratic equations, if they exist
(i) 
(ii) 
Answer 12
Question 13
Solve :
(i) 
and x > 0.
(ii) 
and x < 0.
Answer 13
—-: End of Concise Solutions Quadratic Equations Chapter 5 :——
Return to :- Concise Selina Maths Solutions for ICSE Class-10
Thanks
Please share with your friends
