ML Aggarwal Cubes and Cube Roots Exe-4.1 Class 8 ICSE Ch-4 Maths Solutions. We Provide Step by Step Answer of Exe-4.1 Questions for Cubes and Cube Roots as council prescribe guideline for upcoming board exam. Visit official Website CISCE for detail information about ICSE Board Class-8.
ML Aggarwal Cubes and Cube Roots Exe-4.1 Class 8 ICSE Maths Solutions
| Board | ICSE |
| Publications | Avichal Publishig Company (APC) |
| Subject | Maths |
| Class | 8th |
| Chapter-4 | Cubes and Cube Roots |
| Writer | ML Aggarwal |
| Book Name | Understanding |
| Topics | Solution of Exe-4.1 Questions |
| Edition | 2023-2024 |
Cubes and Cube Roots Exe-4.1
ML Aggarwal Class 8 ICSE Maths Solutions
Page-71
Questions 1. which of the following numbers are not perfect cubes ? give reason in support of your answer.
(i) 648
(ii) 729
(iii) 8640
(iv) 8000
Answer :
(i) 648
648 = 2 × 2 × 2 × 3 × 3 × 3 × 3

648 = (2 × 2 × 2) × (3 × 3 × 3) × 3
Hence, 648 is not a perfect cube.
(ii) 729
729 = 3 × 3 × 3 × 3 × 3 × 3
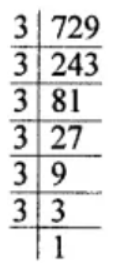
729 = (3 × 3 × 3) × (3 × 3 × 3)
Hence, 729 is a perfect cube.
(iii) 8640
8640 = 2 × 2 × 2 × 2 × 2 × 2 × 3 × 3 × 3 × 5

8640 = (2 × 2 × 2) × (2 × 2 × 2) × (3 × 3 × 3) × 5
Hence, 8640 is not a perfect cube.
(iv) 8000
8000 = 2 × 2 × 2 × 2 × 2 × 2 × 5 × 5 × 5

8000 = (2 × 2 × 2) × (2 × 2 × 2) × (5 × 5 × 5)
Hence, 8000 is a perfect cube.
Question 2. Show that each of the following numbers is a perfect cube. Also, find the number whose cube is the given number:
(i) 1728
(ii) 5832
(iii) 13824
(iv) 35937
Answer :
(i) 1728
1728 = 2 × 2 × 2 × 2 × 2 × 2 × 3 × 3 × 3
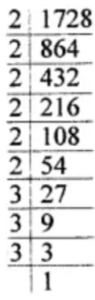
1728 = (2 × 2 × 2) × (2 × 2 × 2) × (3 × 3 × 3)
Hence, 1728 is a perfect cube and its cube root is 2 × 2 × 3 = 12.
(ii) 5832
5832 = 2 × 2 × 2 × 3 × 3 × 3 × 3 × 3 × 3

5832 = (2 × 2 × 2) × (3 × 3 × 3) × (3 × 3 × 3)
Hence, 5832 is a perfect cube and its cube root is 2 × 3 × 3 = 18
(iii) 13824
13824 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 3 × 3 × 3

13824 = (2 × 2 × 2) × (2 × 2 × 2) × (2 × 2 × 2) × (3 × 3 × 3)
Hence, 13824 is a perfect cube and its cube root is 2 × 2 × 2 × 3 = 24.
(iv) 35937
35937 = 3 × 3 × 3 × 11 × 11 × 11

35937 = (3 × 3 × 3) × (11 × 11 × 11)
Hence, 35937 is a perfect cube and its cube root is 3 × 11 = 33
Question 3. Find the smallest number by which each of the following numbers must be multiplied to obtain a perfect cube:
(i) 243
(ii) 3072
(iii) 11979
(iv) 19652
Answer :
(i) 243
243 = 3 × 3 × 3 × 3 × 3
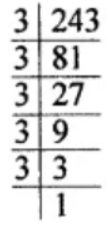
243 = (3 × 3 × 3) × 3 × 3
So, in order to complete in a group of 3’s, one more factor of 3 is needed.
Hence, the smallest number which should be multiplied to 243 in order to make it a perfect cube is 3.
(ii) 3072
3072 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 3

After grouping the prime factors in triplets, it’s seen that factor 2 × 3 are left ungrouped.
3072 = (2 × 2 × 2) × (2 × 2 × 2) × (2 × 2 × 2) × 2 × 3
So, in order to complete them in a group of 3’s we need the factors 2 × 2 × 3 × 3 to be multiplied.
i.e. the factor needed is 2 × 2 × 3 × 3 = 36
Hence, the smallest number which should be multiplied to 3072 in order to make it a perfect cube is 36.
(iii) 11979
11979 = 3 × 3 × 11 × 11 × 11

After grouping the prime factors in triplets, it’s seen that factors 3 × 3 are left without grouping in 3’s.
11979 = 3 × 3 × (11 × 11 × 11)
So, in order to complete in a group of 3’s, one more factor of 3 is needed.
Hence, the smallest number which should be multiplied to 11979 in order to make it a perfect cube is 3.
(iv) 19652
19652 = 2 × 2 × 17 × 17 × 17

After grouping the prime factors in triplets, it’s seen that factors 2 × 2 are left ungrouped in 3’s.
19652 = 2 × 2 × (17 × 17 × 17)
So, in order to complete it in a triplet one more 2 is needed.
Hence, the smallest number which should be multiplied to 19652 in order to make it a perfect cube is 2.
Question 4. Find the smallest number by which each of the following numbers must be divided to obtain a perfect cube:
(i) 1536
(ii) 10985
(iii) 28672
(iv) 13718
Answer :
(i) 1536
1536 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 3

1536 = (2 × 2 × 2) × (2 × 2 × 2) × (2 × 2 × 2) × 3
So, in order to make it a perfect cube, it must be divided by 3.
Hence, the smallest number by which 1536 must be divided to obtain a perfect cube is 3.
(ii) 10985
10985 = 5 × 13 × 13 × 13
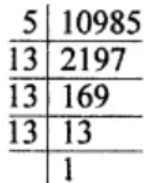
10985 = 5 × (13 × 13 × 13)
So, it must be divided by 5 in order to get a perfect cube.
Hence, the required smallest number is 5.
(iii) 28672
28672 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 7

28672 = (2 × 2 × 2) × (2 × 2 × 2) × (2 × 2 × 2) × (2 × 2 × 2) × 7
So, it must be divided by 7 in order to get a perfect cube.
Hence, the required smallest number is 7.
(iv) 13718
13718 = 2 × 19 × 19 × 19
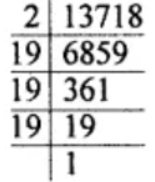
13718 = 2 × (19 × 19 × 19)
So, it must be divided by 2 in order to get a perfect cube.
Hence, the required smallest number is 2.
Question 5. Rahul makes a cuboid of plasticine of sides 3 cm × 3 cm × 5 cm. How many such cuboids will he need to form a cube?
Answer :
Cuboid with dimensions 3 cm × 3 cm × 5 cm
To form into a cube, number of such cuboid required are
= (15/3) x (15/3) x (15/5)
= 5 × 5 × 3
= 75
Hence, the number of cuboids required to make a cube is 75.
Question 6. Find the volume of a cubical box whose surface area is 486 cm2.
Answer :
Surface area of a cubical box = 486 cm2
Surface area of a cubical box = 6 x (side)2
So,
Side = √(486/6) = 9 cm
Now, volume = (Side)3
= (9)3
= 9 × 9 × 9 = 729 cm3
Hence, the volume of the cubical box is 729 cm3.
Question 7. Which of the following are cubes of even natural numbers or odd natural numbers:
(i) 125
(ii) 512
(iii) 1000
(iv) 2197
(v) 4096
(vi) 6859
Answer :
The cube of an even number is even and the cube of an odd number is odd.
Hence,
125, 2197, 6859 are cubes of an odd number, and 512, 1000, 4096 are cubes of an even
Question 8. Write the one’s digit of the cube of each of the following numbers:
(i) 231
(ii) 358
(iii) 419
(iv) 725
(v) 854
(vi) 987
(vii) 752
(viii) 893
Answer :
The cube of a number having 1, 4, 5, 6 or 9 in unit place will end in 1, 4, 5, 6 or 9
And, if the numbers have:
2 in unit place, then it’s cube ends in 8
8 in unit place, then it’s cube ends in 2
3 in unit place then it’s cube ends in 7
7 in unit place then it’s cube ends in 3
0 in unit place then it’s cube ends in 0.
(i) Unit digit of number 231 is 1, hence its cube will end in 1.
(ii) Unit digit of number 358 is 8, hence its cube will end in 2.
(iii) Unit digit of number 419 is 9, hence its cube will end in 9.
(iv) Unit digit of number 725 is 5, hence its cube will end in 5.
(v) Unit digit of number 854 is 4, hence its cube will end in 4.
(vi) Unit digit of number 987 is 7, hence its cube will end in 3.
(vii) Unit digit of number 752 is 2, hence its cube will end in 8.
(viii) Unit digit of numbers 893 is 3, hence its cube will end in 7
Question 9. Find the cubes of the following numbers:
(i) -13
(ii) 3 (1/5)
(iii) −5 (1/7)
Answer :
(i) Cube of -13 = (-13)3
= (-13) × (-13) × (-13)
= -2197
(ii) Cube of 3(1/5)
= (16/5)3 = (16 x 16 x 16)/ (5 x 5 x 5)
= 4096/125
= 32(96/125)
(iii) Cube of −5 (1/7)
= (-36/7)3 = (-36 x -36 x -36)/ (7 x 7 x 7)
= -46656/49
= -136(8/343)
— : End of ML Aggarwal Cubes and Cube Roots Exe-4.1 Class 8 ICSE Maths Solutions :–
Return to – ML Aggarwal Maths Solutions for ICSE Class -8
Thanks
Please Share with Your Friends


