Electric Charge and Fields Numerical on Coulomb’s Law and Superposition Principle ISC Physics Nootan Solutions Ch-1. Step by step solutions of Kumar and Mittal Physics of Nageen Prakashan as council latest prescribe guideline for upcoming exam. Visit official Website CISCE for detail information about ISC Board Class-12 Physics.
Electric Charge and Fields Numerical on Coulomb’s Law and Superposition Principle ISC Physics Nootan Solutions Ch-1
| Board | ISC |
| Class | 12 |
| Subject | Physics |
| Book | Nootan |
| Chapter-1 | Electric Charge and Fields Numerical-I ISC Class-12 Nootan ISC Physics Solutions Ch-1 |
| Topics | Numericals on Coulomb’s Law and Superposition Principle |
| Academic Session | 2025-2026 |
Solved Numericals on Coulomb’s Law and Superposition Principle
Electric Charge and Fields Numerical on Coulomb’s Law and Superposition Principle ISC Physics Nootan Solutions Ch-1
Que-4. Calculate the Coulombian force between a proton and an electron separated by 0.8 x 10^-15 m.
Ans-4 Here, r = 0.8×10^−15
F = [1/(4πɛ0)] x [(q1q2)/r²]
= [9×10^9×1.6×10^−19×1.6×10^−19]/(0.8×10^−15)²
= 360N.
Que-5. Calculate the electrostatic force between two a-particles separated by 3.2 x 10 m.
Ans-5 Here, r = 3.2×10^−15m
Charge on α− particle = 2×1.6×10^−19 = 3.2×10^−19 C
F = [1/(4πɛ0)] x [(q1q2)/r²]
= [9×10^9×3.2×10^−19×3.2×10^−19]/(3.2×10^−15)²
= 90N.
Que-6. The mutual electrostatic force of attraction between two small spheres carrying charges +0.4 µC and -0.8 µC in air is 0.2N. What is the separation between the two spheres?
Ans-6 Electrostatic force on the first sphere, F = 0.2 N
Charge on this sphere, q1 = 0.4 μC = 0.4 × 10−6 C
Charge on the second sphere, q2 = − 0.8 μC = − 0.8 × 10−6 C
Electrostatic force between the spheres is given by the relation,
F = [1/(4πɛ0)] x [(q1q2)/r²]
[1/(4πɛ0)] = 9 x 10^9 Nm²C¯²
Where, ∈0 = Permittivity of free space
r² = (q1q2)/[(F4πɛ0)]
= [9 x 10^9 x 0.4 x 10^-6 x 0.8 x 10^-6]/(0.2)
r² = 1.44 x 10^-4
r = √(144 x 10^-4)
r = 12 x 10¯² = 12cm.
Que-7. How far apart the two electrons be, if the force between them equals the weight of an electron? What in case of protons?
Ans-7 Mass of electron, m = 9.1×10^−31
Weight of electron, W = mg
= 9.1×10^−31×10
= 9.1×10^−30 N
Given,
mg = (1q²)/(4πϵ0r²)
9.1×10^−30 = [9×10^9×(1.6×10^−19)²]/r²
⇒ r² = [9×10^9×2.50×10^−38]/(9.1×10^−30)
= 2.53×10
r² = 25.3
r = √25.3
r ≈ 5m.
F = [1/(4πɛ0)] x [(q1q2)/r²]
e = 1.602×10^−19C
W = mg
Mass of electron, m = 1.67×10^−27kg
Acceleration due to gravity, g = 10m/s²
Weight, W = 1.67×10^−27×10 = 1.67×10^−26 N
F = [1/(4πɛ0)] x [(q1q2)/r²]
[9 x 10^9 x (1.6 x 10^-19)²]/r² = 1.67 x 10^26
r² = [9 x 10^9 x (2.56 x 10^-38)]/(1.67 x 10^26)
r² = [(2.56×9)/1.67] x 10^-38+9+26
r² = 13.796 x 10¯³ = 0.0137
r = √0.0137 = 0.117m
Que-8. Two positive charges distant 0.1 m apart, repel each other with a force of 18 N. If the sum of the charges be 9 micro-coulomb (µC), then calculate their separate values.
Ans-8 Let q1 = q μC = q×10^−6 C
q2 = (9−q)μC
= (9−q)×10^−6 C
As F = [(q1q2)/(4π∈0r²)]
∴ 18 = [q×10^−6 x (9−q)×10^−6×9×10^9]/[(10¯¹)²
18 = (9q−q²)(9/10)
q²−9q+20 = 0, which gives
q = 5 μC and 4 μC
Que-9. The distance between two negatively-charged dust particles is 1 mm and they repel each other with a force of 4.0 x 10^-5 N. If the charge on one particle is 4 times that of the other, then find out the number of electrons charging them separately. The charge on electron is (5/3) x 10^-19 C.
Ans-9 ATQ q1 = 4q2 f = 4.0 x 10^-5
r = 1 x 10^-3 m
According to formula
F = k q1q2/r^2
4.0 x 10^-5 = 9 x 10^9 x 4q2.q2 / (1 x 10^-3)^2
q2 = 10^-10/3
q1 = 4 x 10^-10/3
q = ne => n = q/e
n2 = 10^-10/3 x 3/5×10^-19
=> 2 x 10^8 and n1 = 8 x 10^8
Que-10. Two point-charges of +2 µC and +6 µC repel each other with a force of 12 N. If each is given an additional charge of -4 µC, then what will be the new force?
Ans-10 Given – q1 = 2μC = 2 × 10-6 C, q2 = 6μC = 6 × 10-6 C and F1 = 12 N
Let us suppose the distance between the two charges is r,
The force between them is
⇒ 𝐹1 = [𝑘(2×10^−6)×(6×10−6)]/𝑟²
⇒ 12 = [𝑘x12×10^−12]/𝑟² ———– (1)
Now when an additional charge of -4μC is added to the previous charge, them
q1 = (-4μC + 2μC) = -2μC = -2 × 10-6 C, q2 = (-4μC + 6μC) = 2μC = 2 × 10-6 C
Force between them is
⇒ 𝐹2 = [𝑘(−2×10^−6)×(2×10−6)]/𝑟²
⇒ 𝐹2 = [𝑘x−4×10^−12]/𝑟² ———– (2)
On dividing equation 1 and 2, we get
⇒12/𝐹2 = [(𝑘x12×10^−12)/𝑟²]/[(𝑘−4×10^−12)/𝑟²] = −12/4 = −3
⇒ 𝐹2 = −12/3 = −4𝑁(attractive)
Here negative sign shows that the force is attractive in nature
∴ F2 = 4 N
Que-11. Two identical metallic balls A and B have charges +40 and – 10 µC respectively. The distance between them is 2.0 m. What is the magnitude and type of force acting between them? They are touched to each other and again separated by a distance of 2.0 m from each other. Calculate the new force between them. What will be the force if one ball is connected to earth?
Ans-11 In first case, force:
F = (kQ1Q2)/r²
F = (9×10^9×−10×10^−6×40×10^−6)/2²
F = −0.9N
This force is attractive as it is negative.
In next case, charge on each sphere:
Q = (Q1+Q2)/2
Q = (40−10)/2
Q = 15μC
15μC
in each sphere as charges are distributed uniformly.
Therefore, force is:
F = (9×10^9×15²×10^−12)/2²
F = 0.506N
F ≈ 0.51N
This force is repulsive as it is positive.
Que-12. Two similarly and equally charged identical metal spheres A and B repel each other with a force of 2.0 x 10^-5 N. A third identical, uncharged sphere C is touched with A and then placed at the mid-point between A and B. What is net electric force on C?
Ans-12 Let the charge on each sphere be q then the force on each sphere is
F = (kqq)/r² = (kq²)/r² = 2×10^−5…..(1)
When sphere C is touched by sphere A, charge q gets equally divided between the two.
Thus, FCA = [k(q/2)(q/2)]/(r²/4) = (kq²)/r²
and FCB = [k(q/2)(q)]/(r²/4) = (2kq²)/r²
Net force = FCB−FCA = [(2kq²)/r²] − [(kq²)/r²] = (kq²)/r² = 2×10^−5 N
Que-13. In the given figures are shown three particles A, B and C which are equally charged. The force acting on B due to A is 2.0 x 10^-6 N. Find out in each Fig. (i) force exerted on B by C, (ii) net force on B.
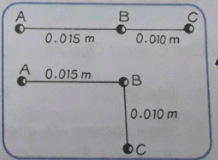
Ans-13 (i) As per Coulomb’s law of electrostatic force we know that the force is given as
F = [(kq1q2)/r²]
2 x 10^-6 = [{9×10^9(q²)}/(0.015)²]
so we have
force exerted by C on B is given as
F = [{9×10^9(q²)}/(0.010)²]
from above equations we have
F/(2×10^-6) = (0.015)²/(0.010)²
so we have
F = 4.5 x 10^-6 N
(ii) Now in first case when all charges are in same line
then net force on the middle charge is given as
Fbc – Fba
F = 4.5 x 10^-6 – 2 x 10^-6
F = 2.5 x 10^-6 N
Now in second case when three charges are placed perpendicular
so here we have
F = √[(Fba)²+(Fbc)²]
F = √(4.5²+2²) x 10^-6
F = 4.92 x 10^-6 N.
Que-14. Two point-charges of 1.0 µC and -0.25 µC are placed in air at a distance of 0.40 m from each other. Find out at which point on the line joining the two charges should a third charge be placed so that no force acts upon it?
Ans-14 Suppose A is 1.0μC and B is −0.25μC
The required point will be outside the two charges and close to smaller charge. Therefore, by coulomb’s law, net force on charge will be zero.
[1/(4πϵ0)] x [(1×q)/(4+x)²]+[1/(4πϵ0)] x [(−0.25)q]/x² = 0
⇒ [1/(4+x)²] = 0.25/x²
⇒ [1/(0.4+x)] = 0.5/x
⇒ 0.2+0.5x = x
⇒ x = 0.4m
Que-15. Two point-charges +9e and +e are placed at a distance of 16 cm from each other. At what point between these charges should a third charge q be placed so that it remains in equilibrium?
Ans-15Let the charge q is placed at a distance x from between charges +9e and +e
Using Coulomb’s law,
(K.9e.q)/x² = (K.q.e)/(16−x)² {F = (Kq1q2)/r²}
[(16−x)²/x] = 19
(16/x)−1 = ±1/3
⇒ 16/x = 4/3
⇒ x = (3×16)/4
∴x=12 cm
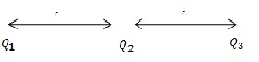
Que-16. Three point-charges 91, 92 and q3 are in line at equal distances. 92 and q3 are opposite in sign. Find the magnitude and sign of q1, if the net force on q3 is zero.
Ans-16 Q2 and Q3 are equal is magnitude but opposite in sign.
∴Q2 and Q3 experience attractive force due to each other. Now Q1 must have sign of Q3 to repel it so that Net force on Q3 is zero
⇒ [−kQ2Q3]/r² = [k(Q1)Q3]/(2r)²
⇒ Q1 = −4Q²
⇒ Q1 = 4 ∣Q3∣
as ∣Q2∣ = ∣Q3∣
Que-17. ABC is an equilateral triangle of side 10 m and D is the mid-point of BC. Charges of +100, 100 and +75 μC are placed at B, C and D respectively. Find the force on a +1 µC charge placed at A.
Ans-17
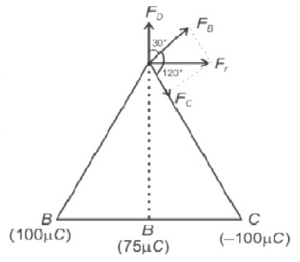
AD = √3/2 x 10 = 5√3
FB = [k(10^-6)(100×10^-6)]/(10)² = k x 10^-12
FC = [k(10^-6)(100×10^-6)]/(10)² = k x 10^-12
FD = [k(10^-6)(100×10^-6)]/(10)² = k x 10^-12
FR = √(FB²+FC²2FBFC Cos120°) = k x 10^-12
F = k√2 x 10^-12
= √2 x 10^-12 x 9 x 10^9
= 9√2 x 10^-3 N.
Que-18. At each of the four corners of a square of side a, a charge +q is placed freely. What charge should be placed at the centre of the square so that the whole system be in equilibrium?
Ans-18

Let charge Q be placed at centre for the system to be in equilibrium
Consider equilibrium of charge q placed at A
F1 = (kq²)/a², F2 = (kq²)/a²
Resultant of F1 and F2, |Fr| = √[{(kq²)/a²}²+{(kq²)/a²}²]
Is along CA, |Fr| = (√2kq²)/a² along CA
F3 = [(kq²)/(√2a)²] = [(kq²)/2a²] along CA
F4 = [(kqQ)/(√2a/2)²] = [(2kqQ)/a²]
Net force F4 = [(√2kq²)/a²] + [(kq²)/2a²] + [(2kqQ)/a²]
For equilibrium, this thin Fn should be zero
Fn = kq/a²[(√2q)+(q/2)+2Q] = 0
(q/2)(2√2+1) = -2Q
Q = -q/4(1+2√2).
— : End Electric Charge and Fields Numerical on Coulomb’s Law and Superposition Principle :–
Return to : – Nootan Solutions for ISC Class-12 Physics
Thanks
Please share with your friends