Electric Charge and Fields Numerical on Electric Dipole Class-12 Nootan ISC Physics Nootan Solutions Ch-1. Step by step solutions of Kumar and Mittal Physics of Nageen Prakashan as council latest prescribe guideline for upcoming exam. Visit official Website CISCE for detail information about ISC Board Class-12 Physics.

Electric Charge and Fields Numerical on Electric Dipole Class-12 Nootan ISC Physics Nootan Solutions Ch-1
| Board | ISC |
| Class | 12 |
| Subject | Physics |
| Book | Nootan |
| Chapter-1 | Electric Charge and Fields Numerical |
| Topics | Numericals on Electric Dipole |
| Academic Session | 2025-2026 |
Numericals on Electric Dipole
Que-26: A system has two charges qA = + 0.25 μC and qB = -0.25 µC at points A (0, 0, -15 cm) and B (0, 0, +15 cm) respectively. Find the total charge and electric dipole moment of the system.
Ans : At A, amount of charge, qA = 2.5 × 10−7C
At B, amount of charge, qB = −2.5 × 10−7 C
Total charge of the system,
q = qA + qB
= 2.5 × 107 C − 2.5 × 10−7 C
= 0
Distance between two charges at points A and B,
d = 15 + 15 = 30 cm = 0.3 m
Electric dipole moment of the system is given by,
p = qA × d = qB × d
= 2.5 × 10−7 × 0.3
= 7.5 × 10−8 C m along positive z-axis
Therefore, the electric dipole moment of the system is 7.5 × 10−8 C m along positive z−axis.
Que-27: Two charges of +2.4µC and -2.4µC are at a distance 2.5 x 10^-3 m apart from each other. Determine the magnitude of the electric field in the broad-side-on position at a distance of 0.30 m from this dipole. If the dipole be rotated through 90°, then what will be the intensity of the field?
Ans: Given:
q = 2.4×10^−6 C
2a = 2.5×10^−3 m ⇒ a = 1.25×10^−3 m
r = 0.30 m
p = q⋅2a
= 2.4×10^−6C × 2.5×10^−3m
= 6×10^−9 C-m.
Now, calculate the electric field E :
E = [1/4πϵ0] ⋅ [p/(r²+a²)^3/2]
E = [9×10^9 ⋅6×10^−9 ]/[(0.30²(1.25×10^−3)²)^3/2]
E = [54×100^0]/[(0.09+1.5625×10^−6)^3/2]
E = 54/(0.0900015625)^3/2
E = 54/0.027001171 ≈ 2000 N/C.
E∥ = [1/(4πϵ0)]⋅(2p/r³)
Using the same dipole moment p:
E∥ = [1/(4πϵ0)]⋅[2⋅6×10^−9 ]/(0.30)³
E∥ = [9×10^9 N⋅12×10^−9]/0.027
E∥ = (108×100^0)/ 0.027
E∥ = 4000 N/C
The magnitude of the electric field in the broad-side-on position at a distance of 0.30 m from the dipole is approximately 2000 N/C.
If the dipole is rotated through 90°, the intensity of the field at the same distance becomes approximately 4000 N/C.
Que-28: Two point-charges of +1µC and -1µC are kept at a distance of 2 cm. They form an electric dipole. This dipole is situated in a uniform electric field of 1 x 10^5 N/C, with dipole moment vector →p making an angle of 30° with the field. Calculate (i) the magnitude of electric dipole moment and (ii) the torque acting on the dipole. (iii) When would be the torque maximum? How much?
Ans: q1 = +1 μC = + 1 x 10^-6 C
q2 = -1 μC = – 1 x 10^-6 C
r = 2 cm = 2 x 10¯² m
E = 1 x 10^5 Newton per coulomb
θ = 30°
(i) The electric dipole moment for a pair of equal & opposite charges is the magnitude of the charges multiplied by the distance between the two.
∴p = q×d
p = 1 x 10^-6 x 2 10¯²
p = 2 x 10^-8
p = 0.2 μC
(ii) We know that
τ = qEsinθ
τ = 1 x 10^-6 x 2 10¯² × sin 30°
τ = 1 x 10^-8
τ = 0.1 Nm
(iii) τmax = pE
= 2 x 10^-8 x 1 x 10^5
τmax = 2 x 10^-3 N-m.
Que-29: An electric dipole, when held at 30° with respect to a uniform electric field of 10^4 N/C, experiences a torque of 9 x 10^-26 N-m. Calculate the moment of the dipole.
Ans: Given : E = 10^4 N/C
t = 9 x 10^-26 N-m
θ = 30°
Torque τ = pEsinθ
⇒ 9×10^−26 = p(10^4)(sin60°)
∴ p = 1.8×10^−29 Cm
Que-30: Two small identical electrical dipoles AB and CD, each of dipole moment ‘p’ are kept at an angle of 120° as shown in the figure. What is the resultant dipole moment of this system is subjected to electric field (→E) directed along +X direction, what will be the magnitude and direction of the torque acting on this?
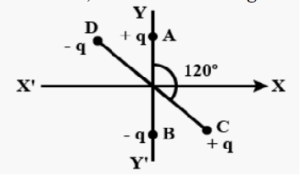
Ans: The two dipoles are placed at an angle of 120°
The dipole moment of AB is directed towards B
and that of cd is directed towards c
Hence,
the resultant dipole moment is given as
R=√[P²+P²+2PPcos120]
= √[2p²−(2p²)/2] = p
when the system is subjected to an electric field ,there is a to sque
acting on the dipole.
The field IS directed towards X-axis .The angle COR in the
above diagram will be 60°.
Hence, the angle between the resultant dipole moment and electric field
is 90° − 60° = 30°
∴ torque on the system is
τ = PEsinθ = PEsin30° = (PE)/2
The direction of torque is perpendicular to both P and E
— : End Electric Charge and Fields Numerical on Electric Dipole Class-12 Nootan ISC Physics Nootan Solutions Ch-1 :–
Return to : – Nootan Solutions for ISC Class-12 Physics
Thanks
Please share with your friends


