Electric Potential and Potential Difference Numerical Class-12 Nootan ISC Physics Solutions Ch-3. Step by step solutions of Kumar and Mittal Physics of Nageen Prakashan as council latest prescribe guideline for upcoming exam. Visit official Website CISCE for detail information about ISC Board Class-12 Physics.

Electric Potential and Potential Difference Numerical Class-12 Nootan ISC Physics Solutions Ch-3
| Board | ISC |
| Class | 12 |
| Subject | Physics |
| Book | Nootan |
| Chapter-3 | Electric Potential |
| Topics | Electric Potential and Potential Difference Numerical |
| Academic Session | 2025-2026 |
Electric Potential and Potential Difference Numerical
Que-1: The amount of work done in bringing a charge of 1.3 x 10^-7 C from infinity to a point in an electric field is 6.5 × 10^-5 J. Find the electric potential at the point.
Ans-1: W = 6.5 x 10^-5 J
Q = 1.3 x 10^-7 C
V = ?
V = W/Q
= (6.5 x 10^-5)/(1.3 x 10^-7)
V = 500V.
Que-2: How much work is done in bringing a charge of 2.5 x 10^-6 C from one point to another, if the potential difference between the two points is 4 V?
Ans-2: Q = 2.5 x 10^-6 C
ΔV = 4V
W = ΔV x Q
= 4 x 2.5 x 10^-7
W = 1.0 x 10^-5 J.
Que-3: 5 J work is done in moving a positive charge of 0.5 C between two points. Find the PD between the points.
Ans-3: W = 5 J
Q = 0.5 C
ΔV = ?
ΔV = W/Q
ΔV = 5/0.5
ΔV = 10 V
Que-4: Compute electric potential at a distance of 0.1 m from a point charge of 4 x 10^-9 C.
Ans-4: Q = 4 x 10^-9 C
r = 0.1 m
According to formula Potential due to point charge at distance r
V = [1/(4πε0)] x Q/r
= [9 x 10^9 x 4 x 10^-9]/0.1
= 36/0.1 = 360 V.
Que-5: A wire is bent in a circle of radius 10 cm. It is given a charge of 250 µC which spreads on it uniformly. What is the electric potential and intensity of field at its center?
Ans-5: Electric field at the center of ring
V = [1/(4πε0)] x Q/r
V = [9 x 10^9 x 250 x 10^-6]/(10 x 10^-2)
V = 2.25 x 10^7 V.
Que-6: Calculate in the given figure: (i) electric potentials at points A and B, (ii) work done in taking the same amount of negative charge from A to B, (OA = 0.10 m, OB = 0.20 m).
Ans-6: Potential at A
VA = [1/(4πε0)] x Q/r
[9 x 10^9 x 10 x 10^-12]/0.1
VA = 0.9 V
Again, VB = [9 x 10^9 x 10 x 10^-12]/0.2
VB = 0.45 V
Work done in taking -10 x 10^-12 μC charge from A to B
W = (VB-VA)Q
W = (0.45-0.9) x (-10 x 10^-12)
W = 4,5 x 10^-12 J.
Que-7: A charge A of 8.0 µC is situated at a distance of 1.00 metre from a charge B of -2.0 µC, as shown. Calculate the potential at the mid-point C between A and B. Also calculate the potential at D which is at a distance of 0.80 m from A and 0.20 m from B. How much work will be done in taking 0.02 µC of charge from D to C?
Ans-7: Potential in scalar quantity therefore it should be directly added with sign
∴ Potential at C = [1/(4πε0)] [{(8 x 10^-6)/0.5} + {(-2 x 10^-6)/0.5}]
[9 x 10^9 x 2 x 10^-6]/0.5 (4±1) = 1.08 x 10^5 V
again Potential at D = [1/(4πε0)] [{(8 x 10^-6)/0.8} + {(-2 x 10^-6)/0.2}]
= 9 x 10^9 x 0 = 0 V
again W = (VC-VD) x Q
W = (1.08 x 10^5 – 0) x (0.02 x 10^-6)
W = 2.16 x 10^-3 J.
Que-8: Two charges +20 µC and -10 µC are 6 cm apart. Find electric potential at a point distant 4 cm on the right bisector of the line joining the charges.
Ans-8:
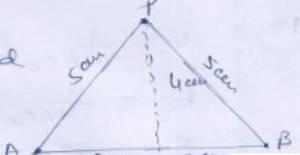
Potential at required point P will be sum of the potential due to both charges at A and B
V = = [1/(4πε0)] [{(20 x 10^-6)/(5 x 10^-2)} + {(-10 x 10^-6)/(5 x 10^-2)}]
V = [9 x 10^9 x 10^-6]/(5 x 10^-2) [20-10]
18 x 10^6 V.
Que-9: The potential due to a point charge at a distance of 0.3 m is 10^3 V. What will be the electric field intensity due to the same charge at a distance of 0.4 m?
Ans-9: Let the point charge is q
then V = [1/(4πε0)] x Q/r
Q = V(4πε0)r
10^3 x (1/9) x 10^-9 x 0.3 {(4πε0) = 1/9 x 10^-9}
= 1/3 x 10^-7 C
again E = [1/(4πε0)] x Q/r
= 9 x 10^9 x (1/3) x 10^-7 x [1/(0.4 x 0.4)]
= 1875 V/m.
Que-10: The electric field at a point due to a point charge is 20 N/C and the electric potential at that point is 10 J/C. Calculate the distance of the point from the charge and the magnitude of the charge.
Ans-10: V = [1/(4πε0)] x q/r
E = [1/(4πε0)] x Q/r²
E/V = 1/r
20/10 = 1/r
r = 0.5 m
V = [9 x 10^9 x q]/0.5 = 10
q = (10 x 0.5)/9 x 10^9
q = 0.55 x 10^-9 C.
Que-11: A point charge of 6.0 x 10^-8 C is situated at the coordinate origin. How much work will be done in taking an electron from the point x = 3 m to x = 6 m?
Ans-11:

W = Δv x q
= (VA-VB)q
= 1/(4πε0) [{(6 x 10^-8)/6} – {(6 x 10^-8)/3}] [-1.6 x 10^-19]
= 9 x 10^9 (1-2) x 10^-8 {-1.6 x 10^-19}
= 9 x 1.6 x 10^-18 J = 1.44 x 10^-17 J.
Que-12: At each corner of an equilateral triangle charges of +250 µC are placed in air. What will be the resultant electric potential at the centroid of the triangle whose distance from each corner is 18 cm?
Ans-12: Electric potential is a scalar therefore it will be added directly
V = 1/(4πε0) [(250 x 10^-6)/(18 x 10^-2)] x 3
= {(9 x 10^9)(250 x 10^-6) x 3/(18 x 10^-2)}
= 375 x 10^5 V = 3.75 x 10^7 V.
Que-13: Electric charges of the same nature and each of 100 µC are placed at the corners of a square having a diagonal of 2 m. Determine the resultant potential at the center of the square.
Ans-13:
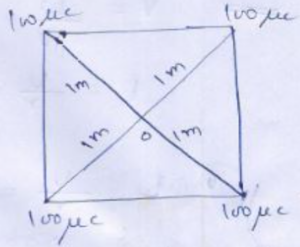
Since diagonals are of 2m therefore each corner will be at a distance of 1m from center. Therefore net potential will be sum of potential of all charges
i.e., V = 1/(4πε0) {(100 x 10^-6)/1} x 4
= 9 x 10^9 x 100 x 10^-6 x 4
= 3.6 x 10^4 V.
Que-14: How much kinetic energy is gained by an electron, initially at rest, when it moves through a potential difference of 1000 V? Leave your answer in Joule.
Ans-14: V = 1000 V
q 1.6 x 10^-19
K = qV
K = 1.6 x 10^-19 x 1000
K = 1.6 x 10^-16 J.
Que-15: An a-particle at rest is accelerated through 10^6 V (i) What will be its kinetic energy? (ii) If a proton be accelerated through the same potential difference, then how much kinetic energy will it gain? (iii) Which particle will gain more velocity if both start from rest?
Ans-15: (i) K.E = W = qV
= 3.2 x 10^-19 x 10^6
= 3.2 x 10^-13 J.
(ii) Proton has charge 1.6 x 10^-19 C
K = 1.6 x 10^-19 x 10^6
K = 1.6 x 10^13 J
(iii) acceleration ∝ 1/m
Since proton is lighter ∝ particle
Therefore, proton has higher acceleration.
Que-16: A test charge ‘q’ is moved without acceleration from A to C along the path from A to B and then from B to C in electric field E as shown in the figure. (i) Calculate the potential difference between A and C. (ii) At which point (A or C) is the electric potential more and why?

Ans-16: (i) Electric field is given by:
E = Ei = (−dV/dx)i
Hence, VC−VA = −∫Edx
VA−VC = −4E
(ii) Electric potential is more at point C as electric field is directed from higher potential region to lower potential region.
Que-17: The two graphs drawn below, show the variations of electrostatic potential (V) with 1/r (r being the distance of field point from the point charge) for two point charges q1 and 42.
(i) What are the signs of the two charges?
(ii) Which of the two charges has the larger magnitude and why?
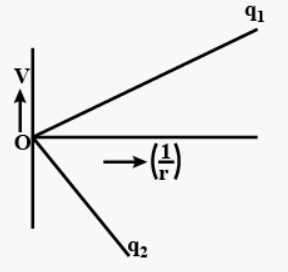
Ans-17: (i) The potential due to positive charge is positive and due to negative charge, it is negative, so is 𝑞1 positive and 𝑞2 is negative.
𝑉 = [1/(4𝜋𝜀𝑜)] x 𝑞/𝑟
(ii) The graph between V and 21/r is a straight line passing through the origin with slope 𝑞/4𝜋𝜀𝑜.
As the magnitude of slope of the line due to charge 𝑞2 is greater than that due to 𝑞1 , 𝑞2 has larger magnitude.
— : End Electric Potential and Potential Difference Numerical Class-12 Nootan ISC Physics Solutions Ch-3 . :–
Return to : – Nootan Solutions for ISC Class-12 Physics
Thanks
Please share with your friends


