ML Aggarwal Triangles Exe-10.4 ICSE Class 9 Maths Solutions

ML Aggarwal Triangles Exe-10.4 ICSE Class 9 Maths Solutions Ch-10. Step by Step Answer of Exercise-10.4 of Triangles of ML Aggarwal for ICSE Class 9th Mathematics Questions. Visit official website CISCE for detail information about ICSE Board Class-9.

ML Aggarwal Triangles Exe-10.4 ICSE Class 9 Maths Solutions

Board	ICSE
Subject	Maths
Class	9th
Chapter-10	Triangles
Topics	Solution of Exe-10.4 Questions
Academic Session	2024-2025

Solution of Exe-10.4 Questions

ML Aggarwal Triangles Exe-10.4 ICSE Class 9 Maths Solutions Ch-10

Question 1. In ∆PQR, ∠P = 70° and ∠R = 30°. Which side of this triangle is longest? Give reason for your answer.

Answer :  In ∆PQR, ∠P = 70^o, ∠R = 30^o

But ∠P + ∠Q + ∠R = 180^o

⇒ 100^o + ∠Q = 180^o

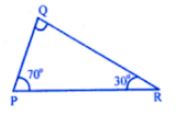
⇒ ∠Q = 180^o – 100^o = 180^o

⇒ ∠Q = 80^o the greatest angle

Its opposite side PR is the longest side

Question 2. Show that in a right angled triangle, the hypotenuse is the longest side.

Answer : in right angled ∆ABC, ∠B = 90^o

To prove: AC is the longest side

Proof: in ∆ABC,

∠B = 90^o

∠A and ∠C are acute angles

That is less then 90^o

∠B is the greatest angle

Or ∠B> ∠C and ∠B> ∠A

AC > AB and AC > BC

Hence AC is the longest side

Question 3. PQR is a right angle triangle at Q and PQ : QR = 3:2. Which is the least angle.

Answer :

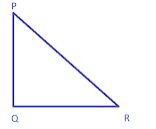
Here, PQR is a right angle triangle at Q. Also given that

PQ : QR = 3:2

Let PQ = 3x, then, QR = 2x

It is clear that QR is the least side,

Then, we know that the least angle has least side

Opposite to it.

Therefore, ∠P is the least angle

Question 4. In ∆ ABC, AB = 8 cm, BC = 5.6 cm and CA = 6.5 cm. Which is 

(i) the greatest angle ?
(ii) the smallest angle ?

Answer :

Given that,

AB = 8 cm, BC = 5.6 cm, CA = 6.5 cm.

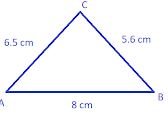
Here, AB is the greatest side. (The greatest side has greatest angle opposite to it)

Then ∠C is the least angle.

Also, BC is the least side.

Then ∠A is the least angle.

Question 5. In ∆ABC, ∠A = 50°, ∠B= 60°, Arrange the sides of the triangle in ascending order

Answer :

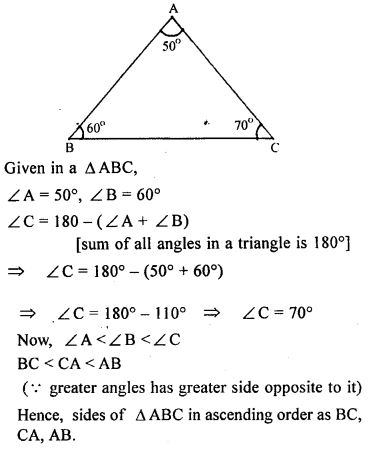
Question 6.  In figure given alongside, ∠B = 30°, ∠C = 40° and the bisector of ∠A meets BC at D. Show

(i) BD > AD
(ii) DC > AD
(iii) AC > DC
(iv) AB > BD

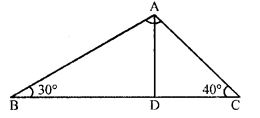
Answer :

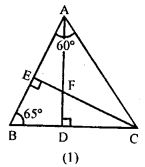
Question 7.  In the figure (1) given below, AD bisects ∠A. Arrange AB, BD and DC in the descending order of their lengths.

Answer : $(a)$△ ABC, AD bisects ∠A,

In △ABC,
Sum of angles = 180
∠A + ∠B + ∠C = 180
∠A + 60 + 40 = 180
∠A = 80º
∠BAD = ∠DAC = 40º
∠A = 80º, ∠C = 40º

Since, ∠A > ∠C
BC > AB (Sides opposite greater angles is greater) (1)
In △ADC
∠ACD = ∠DAC = 40º

Thus, AD=DC (Isosceles triangle property)
Now, In △ABD
Sum of angles = 180
∠ABD + ∠ADB + ∠BAD = 180
60 + ∠ADB + 40 = 180
∠ADB = 80º

∠ABD = 60º and △ADB = 80º

Since, ∠ABD > ∠ADB
Thus, AD > AB
or DC > AB (Since, AD = DC) (2)
and we know BC = BD + DC
Hence, BC > DC (3)
Hence, from (1), (2) and (3)
BC > DC > AB

Question 8. (a) In the figure (1) given below, prove that (i) CF> AF (ii) DC>DF.

(b) In the figure (2) given below, AB = AC.
Prove that AB > CD.

(c) In the figure (3) given below, AC = CD. Prove that BC < CD.

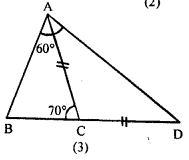
Answer : (a)  (i) In triangle ABC

ACB=180-60-65=55

In triangle BEC

BCE=180-90-65=25

SO, ACE=55-25=30

Angle opposite CF=90

Angle opposite AF=30

Hence CF>AF as angle opp CF is greater than the angle opposite AF

(ii) In triangle DFC

DFC= 180-90-DCF        ( DCF=25)

DFC=180-90-25=65

Angle opposite DC=65

Angle opp DF= 25

Hence, DC>DF for the same reason as in the first part

(b) Update soon

Question 9. (a) In the figure (i) given below, ∠B < ∠A and ∠C < ∠D. Show that AD < BC.

(b) In the figure (ii) given below, D is any point on the side BC of ∆ABC. If AB > AC, show that AB > AD.

Answer : (a)  In figure, ∠B <  ∠A and ∠C <  ∠D.

To Prove: AD <  BC

Proof: ∠B <  ∠A    | Given
∴ ∠A >  ∠B
∴ OB >  OA    …(1)
| Side opposite to greater angle is longer
∠C <  ∠D    | Given
∴ ∠D >  ∠C
∴ OC >  OD    …(2)
| Side opposite to greater angle is longer
From (1) and (2), we get
OB + OC >  OA + OD
⇒ BC > AD
⇒ AD < BC.

(b) AB > AC We know that,

The angle opposite to greater side is greater than the other……….

Means, ang. ACB > ang. ABC.

NOW, angle  ADB = angle  ACB + angle  DAC

ADB > ang. ABC

OR, AB> AD......

Because, AB is opposite side of angle ADB which is greater than ang. ABC.

Question 10. 

(i) Is it possible to construct a triangle with lengths of its sides as 4 cm, 3 cm and 7 cm? Give reason for your answer,
(ii) Is it possible to construct a triangle with lengths of its sides as 9 cm, 7 cm and 17 cm? Give reason for your answer.
(iii) Is it possible to construct a triangle with lengths of its sides as 8 cm, 7 cm and 4 cm? Give reason for your answer.

Answer: (i) Length of sides of a triangle are 4 cm, 3 cm and 7 cm

We know that sum of any two sides of a triangle is greatar than its third side But 4 + 3 = 7 cm
Which is not possible
Hence to construction of a triangle with sides 4 cm, 3 cm and 7 cm is not possible.

(ii) Length of sides of a triangle are 9 cm, 7 cm and 17 cm

We know that sum of any two sides of a triangle is greater than its third side Now 9 + 7 = 16 < 17 ∴ It is not possible to construct a triangle with these sides.

(iii) Length of sides of a triangle are 8 cm, 7 cm and 4 cm We know that sum of any two sides of a triangle is greater than its third side Now 7 + 4 = 11 > 8

Yes, It is possible to construct a triangle with these sides.

—  : End of ML Aggarwal Triangles Exe-10.4 Class 9 ICSE Maths Solutions :–

Return to :- ML Aggarawal Maths Solutions for ICSE  Class-9

Thanks

Please Share with Your Friends