Expansions Class 9 OP Malhotra Exe-3B ICSE Maths Solutions

Expansions Class 9 OP Malhotra Exe-3B ICSE Maths Solutions Ch-3. We Provide Step by Step Solutions / Answer of Questions on Expansions OP Malhotra Maths. Visit official Website CISCE  for detail information about ICSE Board Class-9 Mathematics..

Expansions Class 9 OP Malhotra Exe-3B ICSE Maths Solutions Ch-3

Board	ICSE
Publications	S Chand
Subject	Maths
Class	9th
Chapter-3	Expansions
Writer	OP Malhotra
Exe-3B
Edition	2025-2026

Exercise – 3B

Expansions Class 9 OP Malhotra Exe-3B ICSE Maths Solutions Ch-3

Que-1: Find the value of:
(i) a² + b² when a + b = 9, ab = 20
(ii) p² + q² if p – q = 6 and p + q = 14
(iii) mn if m + n = 8, m – n = 2
(iv) x² + (1/x²) and x⁴ + (1/x⁴) if x + (1/x) = 3
(v) x – (1/x) and x² – (1/x²) if x + (1/x) = √5

Sol: (i) a + b = 9, ab – 20
= a² + b² = (a + b)² – 2ab
= (9)² – 2 x 20
= 81 – 40 = 41

(ii) p – q = 6, p + q = 14
2 (p² + q²) = (p + q)² + (p – q)²
= (14)² + (6)²
= 196 + 36 = 232
∴ p² + q² = 232/2 = 116

(iii) m + n = 8, m – n = 2
4mn = (m + n)² – (m – n)²
= (8)² – (2)² = 64 – 4 = 60
∴ mn = 60/4 = 15

(iv) {x + (1/x)} = 3
Squaring both sides,
{x + (1/x)}² = 3²
x² + {2×x×(1/x)} + (1/x)² = 9
x² + 2 + (1/x²) = 9
x² + (1/x²) = 9-2
x² + (1/x²) = 7
Squaring again,
{x² + (1/x²)}² = 7²
x^4 + (1/x^4) + 2 = 49
x^4 + (1/x^4) = 49-2
x^4 + (1/x^4) = 47.

(v) x + 1x = √5
Squaring both sides,

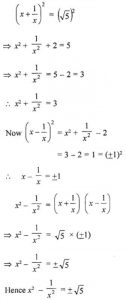
Que-2: (i) a² + b² + c² if a + b + c = 17 and ab + bc + ca = 30.
(ii) ab + be + ca, a + b + c = 15 and a² + b² + c² = 77
(iii) a + b + c if a² + b² + c² = 50 and ab + bc + ca = 47.

Sol: (i) a + b + c = 17
Squaring both sides,
(a + b + c)² = (17)²
⇒ a² + b² + c² + 2 (ab + bc + ca) = 289
⇒ a²+ b² + c² + 2 x 30 = 289
⇒ a² + b² + c² + 60 = 289
⇒ a² + b² + c² = 289 – 60 = 229
∴ a² + b² + c² = 229

(ii) a + b + c = 15 and a² + b² + c² = 77
a + b + c = 15
Squaring both sides,
(a + b + c)² = (15)²
a² + b² + c² + 2 (a + bc + ca) = 225
⇒ 77 + 2 (ab + bc + ca) = 225
⇒ 77 + 2 (ab + bc + ca) = 225
⇒ 2 (a + bc + ca) = 225 – 77 = 148
⇒ ab + bc + ca = 148/2 = 74
∴ ab + bc + ca = 74

(iii) a² + b² + c² = 50, and ab + be + ca = 47
(a + b + c)² = a² + b² + c² + 2 (ab + bc + ca)
= 50 + 2 x 47 = 50 + 94
= 144 = (± 12)²
∴ a + b + c = ± 12

Que-3: (i) 8x³ + 84x²y + 294xy² + 343y³ if x = 1, y = 2
(ii) 27x³ – 27x²y + 9xy2 – y³ if x = 2, y = 1

Sol: (i) x = 1, y = 2
8x³ + 84x²y + 294xy² + 343y³
= (2x)³ + 3 (2x)² x 7y + 3 x 2x × (7y)² + (7y)³
= (2x + 7y)³ = (2 x 1 + 7 x 2)³
= (2 + 14)³ = (16)³ = 4096

(ii) x = 2, y = 1
27x³ – 27x²y + 9xy² – y³
= (3x)³ – 3 (3x)² y + 3 (3x)y² – (y)³
= (3x – y)² = (3 x 2 – 1)³
= (6 – 1)³ = (5)³ = 125

Que-4: (i) a³ + b³ if a + b = 3 and ab = 2
(ii) x³ + (1/x³) if (x + (1/x)) = 3
(iii) x³ – (1/x³) if x² + (1/x²) = 18
(iv) x³ + (1/125x³) if x²+(1/25x²) = 8*(3/5)

Sol: (i) a + b = 3, ab = 2
a³ + b² = (a + b)³ – 3ab (a – b)
= (3)³ – 3 x 2 x 3
= 27 – 18 = 9

(ii) x + (1/x) = 3
x³ + (1/x³) = (x + (1/x³) – 3(x + (1/x))
= (3)³ – 3 x 3
= 27 – 9 = 18.

(iii) x² + (1/x²) = 18
Subtracting 2 from both sides
{x² + (1/x²)} – 2 = 18 – 2
{x – (1/x)}² = 16 = (±4)²
x – (1/x) = 4
Now,
x³ – (1/x³) = {x – (1/x)}³ + 3{x-(1/x)}
When {x – (1/x)} = 4
= 4³ + (3×4)
= 64 + 12 = 76
x³ – (1/x³) = {x – (1/x)}³ + 3{x-(1/x)}
= (-4)³ + 3(-4)
= -64 – 12 = -76
{x³ – (1/x³)} = ±76.

(iv) x² + (1/25x²) = 8*(3/5) = 43/5
(x)² + {1/(5x)²} = 43/5
Completing the left hand sides, a complete
square adding 2 × x × (1/5x) i.e., 25 both sides

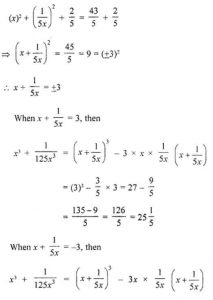
= (-3)³ – (3/5)(-3)
= -27 + (9/5)
= (-135+9)/5
= -126/5 = -25*(1/5)
Hence,
x³ + (1/125x³) = ±25*(1/5).

Que-5: Evaluate:
(i) 102 x 98
(ii) 1003² – 997²
(iii) (10)³ – (5)³ – (5)³

Sol:  (i) 10² x 98
= (100 + 2) (100-2) {∵ {a + b)(a – b) = a² – b²)}
= (100)² – (2)²
= 10000 – 4
= 9996

(ii) (1003)² – (997)²
= (1003 + 997) (1003 – 997) {∵ a² – b² = (a + b) (a – b)}
= 2000 x 6 = 12000

(iii) (10)³ – (5)³ – (5)³ = (10)³ + (- 5)³ + (- 5)³
Let 10 = a, – 5 = b, – 5 = c and a + b + c – 10 – 5 – 5 = 0
∵ a + b + c = 0. then a³ + b³ + c³ = 3abc
⇒ (10)³ – (5)³ – (5)³
= 3 x 10 x (- 5) (- 5)
= 750.

— : End of Expansions Class 9 OP Malhotra Exe-3B ICSE Maths Ch-3 Solutions :–

Return to :–  OP Malhotra S Chand Solutions for ICSE Class-9 Maths

Thanks

Please Share with Your Friends