Kirchhoff’s Laws Numerical Class-12 Nootan ISC Physics Ch-6 DC Circuits and Measurements. Step by step solutions of Kumar and Mittal Physics of Nageen Prakashan as council latest prescribe guideline for upcoming exam. Visit official Website CISCE for detail information about ISC Board Class-12 Physics.

Kirchhoff’s Laws Numerical Class-12 Nootan ISC Physics DC Circuits and Measurements
| Board | ISC |
| Class | 12 |
| Subject | Physics |
| Book | Nootan |
| Chapter-6 | DC Circuits and Measurements. |
| Topics | Numericals on Kirchhoff’s Laws |
| Academic Session | 2025-2026 |
Numericals on Kirchhoff’s Laws
Class-12 Nootan ISC Physics Ch-6 DC Circuits and Measurements
Que-17. Determine current in 3 Ω resistance and potential difference between A and B in the adjoining circuit diagram.
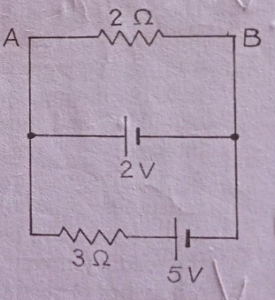
Ans-17 The resultant voltage = 5 V – 2 V
= 3 V
Since the 3-ohm resistor is in a series connection so the current is constant,
Current in 3 ohm resistor = 3 V / 3
= 1 A
Now, we can observe that the 2-ohm resistor is in parallel to the 2 V voltage source. Hence, we can understand that the voltage between A and B points will be the same as the voltage across the resistor, as per the third bullet point.
So, the resistance across A and B = 2 V
Que-18. In the circuit shown in figure, E1 = 17 V, E2 = 21 V R1 = 2 Ω, R2 = 3 Ω and R3 = 5 Ω. Using Kirchhoff’s laws, find currents flowing through resistors R1, R2 and R3 (internal resistance of each of the batteries is negligible).

Ans-18 Let us suppose that I1 current flows through E1
and I2 current flows through E2
Using Kirchhoff’s Law:
I1R1+(I1+I2)R3 = E1
(I1×2) + {(I1+I2)5} = 17
2I1+5I1+5I2 = 17
7I1+5I2 = 17
I1R2+(I1+I2)R3 = E2
(I2×3)+{(I1+I2)5} = 21
5I1+8I2 = 21
35I1+25I2 = 85
35I1+56I2 = 147
−31I2 = −62
I2 = 2 amp
7I1+5I2 = 17
7I1+10 = 17
7I1 = 7
So, I1 = 1 amp
Total I = I1 + I2
I = 1+2 = 3 amp.
Que-19. In the given circuit E1 and E2 are two cells of emfs 2 V and 3 V respectively, having negligible internal resistances. Applying Kirchhoff’s laws of electrical networks, find the values of I1 and I2.
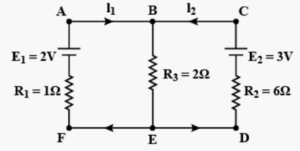
Ans-19 Applying kirchhoff law in loop AFEBA
2-1i1-(i1+i2)2 = 0
3i1+2i2 = 2 ………. (i)
and in loop CBEDC
(i1+i2)2+(i2 x 6)-3 = 0
2i1 + 8i2 = 3 ……… (ii)
Solving (i) and (ii) we get,
i1 = 0.5 A and i2 = 0.25 A.
Que-20. Two cells E1 and E2 of emf’s 4 V and 2 V respectively, each having an internal resistance of 2 Ω send current in an external resistance of 8 Ω. Find the magnitudes and the directions of currents I1, and I2 flowing through the cells E1 and E2.
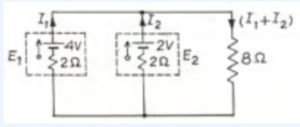
Ans-20 Applying kirchhoff law
8(i1+i2)+2i2 = 2
4i1+5i2 = 1 ……….(i)
8(i1+i2)+2i2 = 4
5i1+4i2 = 2 ………..(ii)
Solving (i) and (ii) we have,
i1 = 2/3 A
i2 = -1/3 A.
Que-21. Two cells of emf’s 6 V and 12 V and internal resistances 1 Ω and 2 Ω respectively are connected in parallel so as to send current in the same direction through an external resistance of 15 Ω. Draw the circuit diagram. Using Kirchhoff’s laws, calculate current through each branch of the circuit and PD across the 15 Ω resistance.
Ans-21
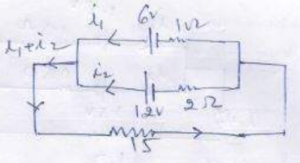
Applying kirchhoff law
-6 + (i1+i2)15 + 1 x i1 = 0
16i1 + 15i2 = 6 ………. (i)
-12 + (i1+i2)15 + 2i2 = 0
15i1 + 17i2 = 12 ………. (ii)
Multiply by 15 in eqn (i) and by 16 in eqn (ii) we get
240i1 + 225 i2 = 90 ……(iii)
240i1 + 272i2 = 192 ………. (iv)
On solving (iii) and (iv) we get,
-47i2 = -102
i2 = 102/47 A
Putting the value of i2 in eqn (i) we get,
16i1 + 15(102/47) = 6
i1 = 6 – (1530/47) = -78/47 A.
Now current through 15Ω resistance
= (102/47) – (78/47) = 24/47
P.D. across 15Ω resistance
V = iR
= (24/47) x 15 = 7.66 V.
Que-22. Two cells A and B, each having emf 1.5 V and internal resistances 1.5 Ω and 0.5 Ω respectively, are joined in parallel with a 1.0 Ω resistor. Calculate currents drawn from the cells and their terminal PD’s.
Ans-22
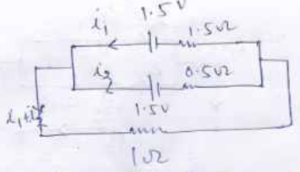
Applying Kirchhoff law
-1.5 + (i1+i2)1 + (i1 x 1.5) = 0
2.5i1 + i2 = 1.5 ……. (i)
and -1.5 + (i1+i2)1 + (i1 x 0.5) = 0
i1 + 1.5i2 = 1.5 ……… (ii)
Multiply by 2 in eqn (i) and by 5 in eqn (ii) we get,
5i1 + 2i2 = 3 ………. (iii)
5i1 + 7.5i2 = 7.5 ……… (iv)
On solving eqn (iii) and (iv) we get,
-5.5i2 = -4.5
i2 = 4.5/5.5 = 9/11 A
again i1 + 1.5i2 = 1.5
i1 + (45/55)x1.5 = 1.5
i1 = 1.5 – (45/55)x1.5
i1 = 1.5 {(55-45)/55} = 15/55 = 3/11 A.
Now i1 + i2 = (9/11) + (3/11) = 12/11 A
P.D. across 1Ω = (12/11) x 1 = 12/11 V.
this will same across cell also because the are in parallel.
Que-23. Calculate the currents I1, I2 and I3 in the given circuit. The cells have negligible internal resistances.
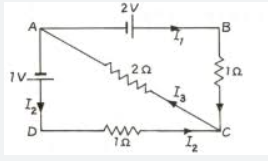
Ans-23 Applying kirchhoff law
-2 + (i1x1) + 2i3 = 0
i1 + 2(i1+i2) = 2 {i3 = i1 +i2}
3i1 + 2i2 = 2 …….. (i)
-1 + (i2x1) + 2i3 = 0
-1 + i2 + 2i2 + 2i2 = 0
2i1 + 3i2 = 1 ……….. (ii)
Multiply by 2 in eqn (i) and by 3 in eqn (ii) we get,
6i1 + 4i2 = 4 ………. (iii)
6i1 + 9i2 = 3 ………. (iv)
On solving eqn (iii) and (iv) we get,
-5i2 = 1
i2 = -1/5 = -0.2 A.
from eqn (ii)
2i1 + 3(-0.2) = 1
2i1 = 1.6
i1 = 0.8
i3 = i1 + i2
i3 = 0.8 – 0.2 = 0.6 A.
Que-24. In the given circuit, assuming point A to be at zero potential, use Kirchhoff’s rule to determine the potential at point B.
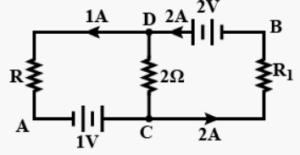
Ans-24 In 1st loop
−R+1+2 = 0
⇒ R = 3Ω
In 2nd loop
−2R1+2−2 = 0
⇒ R1 = 0
Now going from point A to B viac .
VA+1−0 = VB
⇒ VB = 1V
Que-25. Using Kirchhoff’s rules, determine the value of unknown resistance R in the circuit, so that no current flows through 4 Ω resistance. Also, find the potential difference between points A and D.

Ans-25 Applying Kirchhoff’s second law in closed mesh AFEBA ,
9−6 = I×1 + I×1 + 4×0 = 0 (current in 4Ω is given zero)
or 3 = 2I
or I = 3/2 = 1.5A
now in closed mesh AFEDCBA ,
9−3 = I(1+1) + IR
or 6 = 1.5×2 + 1.5R
or 6 = 3+1.5R
or R = 3/1.5 = 2Ω
now from point A to point D , (applying Kirchhoff’s law for linear part AFED)
VA−I(1+1) = VD
or VA−VD = 1.5×2 = 3V.
— : End of Kirchhoff’s Laws Numerical Class-12 Nootan ISC Physics Ch-6 DC Circuits and Measurements. :–
Return to : – Nootan Solutions for ISC Class-12 Physics
Thanks
Please share with your friends