ML Aggarwal Linear Inequation Exe-4 Class 10 ICSE Maths Solutions

ML Aggarwal Linear Inequation Exe-4 Class 10 ICSE Maths Solutions . We Provide Step by Step Answer of Exe-4 Questions for Linear Inequation as council prescribe guideline for upcoming board exam.  Visit official Website CISCE  for detail information about ICSE Board Class-10.

ML Aggarwal Exe-4 Linear Inequation Class 10 ICSE Maths Solutions

Board	ICSE
Subject	Maths
Class	9th
Chapter-4	Linear Inequation
Writer / Book	Understanding
Topics	Solutions of Exe-4
Academic Session	2024-2025

ML Aggarwal Linear Inequation Exe-4 Class 10 ICSE Maths Solutions

Question -1. Solve the inequation 3x -11 < 3 where x ∈ {1, 2, 3,……, 10}. Also represent its solution on a number line

Answer :

3x – 11 < 3 => 3x < 3 + 11 => 3x < 14 x < (14/3)
But x ∈ 6 {1, 2, 3, ……., 10}
Solution set is (1, 2, 3, 4}.

Solution set on number line

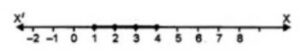
Question- 2. Solve 2(x – 3)< 1, x ∈ {1, 2, 3, …. 10}

Answer :

2(x – 3) < 1 => x – 3 < 1/2 => x < 1/2 + 3 => x < 3(1/2)
But x ∈ {1, 2, 3 …..10}

Solution set = {1, 2, 3}

Question -3. Solve : 5 – 4x > 2 – 3x, x ∈ W. Also represent its solution on the number line.

Answer:

5 – 4x > 2 – 3x
– 4x + 3x > 2 – 5
=> – x > – 3
=> x < 3
x ∈ w,
solution set {0, 1, 2}

Solution set on number line:

Question- 4. List the solution set of 30 – 4 (2.x – 1) < 30, given that x is a positive integer.

Answer :

30 – 4 (2x – 1) < 30
30 – 8x + 4 < 30
– 8x < 30 – 30 – 4
– 8x < – 4 x > (-4/-8)
=> x > 1/2
x is a positive integer
x = {1, 2, 3, 4…..} Ans.

Question -5. Solve : 2 (x – 2) < 3x – 2, x ∈ { – 3, – 2, – 1, 0, 1, 2, 3} .

Answer:

2(x – 2) < 3x – 2
=> 2x – 4 < 3x – 2
=> 2x – 3x < – 2 + 4
=> – x < 2
=> x > – 2
Solution set = { – 1, 0, 1, 2, 3} Ans.

Question -6. If x is a negative integer, find the solution set of 2/3+1/3 (x + 1) > 0.

Answer :

2/3+1/3 x + 1/3 > 0
=> 1/3 x + 1 > 0
=> 1/3 x > – 1

⇒ x > – 1 × 3/1 ⇒ x > – 3

x is a negative integer
Solution set = {- 2, – 1} Ans.

Question -7. Solve x – 3 (2 + x) > 2 (3x – 1), x ∈ { – 3, – 2, – 1, 0, 1, 2, 3}. Also represent its solution on the number line.

Answer :

x – 3 (2 + x) > 2 (3x – 1)
=> x – 6 – 3x > 6x – 2
=> x – 3x – 6x > – 2 + 6
=> – 8x > 4
=> x < -4/8 => x < -1/2

x ∈ { – 3, – 2, – 1, 0, 1, 2}
.’. Solution set = { – 3, – 2, – 1}

Solution set on Number line:

Question- 8. Given x ∈ {1, 2, 3, 4, 5, 6, 7, 9} solve x – 3 < 2x – 1.

Answer:

x – 3 < 2x – 1
x – 2x < – 1 + 3 => – x < 2 x > – 2
But x ∈ {1, 2, 3, 4, 5, 6, 7, 9}
Solution set = {1, 2, 3, 4, 5, 6, 7, 9} Ans.

Question -9. List the solution set of the inequation

1/2 + 8x > 5x -3/2, x ∈ Z

Answer :

1/2 +8x > 5x -3/2

⇒ 8x – 5x > – 3/2 – 1/2

⇒ 3x > – 2 ⇒ x > – 2/3

∵ x ∈ Z,

∴ Solution set = {0, 1, 2, 3, 4 ,…….}

Question -10. List the solution set of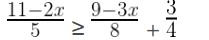
x ∈ N

Answer:

=> 88 – 16x ≥ 45 – 15x + 30
(L.C.M. of 8, 5, 4 = 40}
=> – 16x + 15x ≥ 45 + 30 – 88
=> – x ≥ – 13
=>x ≤ 13
x ≤ N.
Solution set = {1, 2, 3, 4, 5, .. , 13} Ans.

Question -11. Find the values of x, which satisfy the inequation :

 x ∈ N.
Graph the solution set on the number line.

Answer :

, x ∈ N

⇒ – 2 – 1/2 ≤ 1/2 – 2x/3 – 1/2 ≤ 11/6 – 1/2

[By subtracting 1/2 on both sides of inequality]

⇒ – 5/2 ≤ 2x/3 ≤ 8/6

⇒ – 15 ≤ – 4x ≤ 8

⇒ 15 ≥ 4x ≥ – 8

⇒ 15/4 ≥ x ≥ – 2

3.3/4 ≥ x ≥ – 2

But x ∈ N, hence only possible solution for x = {1, 2, 3}

Question -12. If x ∈ W, find the solution set of

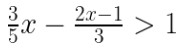
Also graph the solution set on the number line, if possible.

Answer :

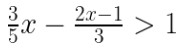
9x – (10x – 5) > 15 (L.C.M. of 5, 3 = 15)
=> 9x – 10x + 5 > 15
=> – x > 15 – 5
=> – x > 10
=> x < – 10
But x ∈ W
Solution set = Φ
Hence it can’t be represented on number line.

Question-13. Solve:

where x is a positive odd integer.

(ii) (2x + 3)/3 ≥ (3x – 1)/4 where x is positive even integer.

Answer :

⇒ x/2 – x/3, ≤ 6 – 5

⇒ (3x – 2x)/6 ≤ 1

⇒ x/6 ≤ 1

⇒ x ≤ 6

∵ x is a positive odd integer

∴ x = {1, 3, 5}

(ii) (2x + 3)/3 ≥ (3x – 1)/4

⇒ 2x/3 + 3/3 ≥ 3x/4 – 1/4

⇒ 2x/3 – 3x/4 ≥ -1/4 – 1

⇒ (8x – 9x)/12 ≥ – 5/4

⇒ -x/12 ≥ -5/4

⇒ x/12 ≤ 5/4

⇒ x ≤ 5/4 × 12

⇒ x ≤ 15

∵ x is positive even integer

∴ x = {2, 4, 6, 8, 10, 12, 14}

Question -14. Given that x ∈ I, solve the inequation and graph the solution on the number line :

Answer :

3 ≥ (3x – 12 + 2x)/6

⇒ 3 ≥ (5x – 12)/6

⇒ 18 ≥ 5x – 12

⇒ 5x – 12 ≤ 18

⇒ 5x ≤ 18 + 12

⇒ 5x ≤ 30

⇒ x ≤ 6

Question -15. Solve : 1 ≥ 15 – 7x > 2x – 27, x ∈ N

Answer :

1 ≥ 15 – 7x > 2x – 27
1 ≥ 15 – 7x and 15 – 7x > 2x – 27

⇒ 7x ≥ 15 – 1 and – 7x – 2x > – 27 – 15

⇒ 7x ≥ 14 and – 9x > – 42

⇒ x ≥2 and – x > – 42/9

⇒ 2 ≤ x and – x > – 14/3 and x < 14/3

2 ≤ x < 14/3

But x ∈ N

∴ Solution set = {2, 3, 4}

Question-16. If x ∈ Z, solve 2 + 4x < 2x – 5 ≤ 3x. Also represent its solution on the number line.

Answer:

2 + 4x < 2x – 5 ≤ 3x

2 + 4x < 2x – 5 and 2x – 5 ≤ 3x

⇒ 4x – 2x < -5 – 2, and 2x – 3x ≤ 5

⇒ 2x < – 7 and – x ≤ 5

⇒ x < – (7/2) and x ≥ – 5 and – 5 ≤ x

∴ – 5 ≤ x < -(7/2)

∵ x ∈ Z

∴ Solution set = {- 5, -4}

Solution set on Number line

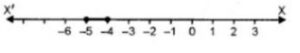
Question -17. Solve : (4x-10)/3 ≤ (5x-7)/2 x ∈ R and represent the solution set on the number line.

Answer :

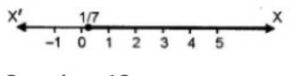
Question -18

Solve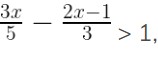

x ∈ R and represent the solution set on the number line.

Answer -18

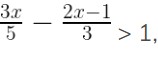
=> 9x – (10x – 5) > 15
=> 9x – 10x + 5 > 15
=> – x > 15 – 5
=> – x > 10
=> x < – 10
x ∈ R.
.’. Solution set = {x : x ∈R, x < – 10}
Solution set on the number line

---

ML Aggarwal Linear Inequation Exe-4 Class 10 ICSE Maths Solutions

page-53

Question -19. Given that x ∈ R, solve the following inequation and graph the solution on the number line: – 1 ≤ 3 + 4x < 23. (2006)

Answer :

We have
– 1 ≤ 3 + 4x < 23 => – 1 – 3 ≤ 4x < 23 – 3 => – 4 ≤ 4x < 20 => – 1 ≤ x < 5, x ∈ R
Solution Set = { – 1 ≤ x < 5; x ∈ R}

Question-20. Solve the following inequation and graph the solution on the number line. (2007)

Answer :

Given

Given,

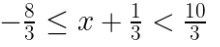
Multiplying by 3, L.C.M. of fractions, we get

– 8 ≤ 3x + 1 < 10

– 8 – 1 ≤ 3x + 1 – 1 < 10 – 1 [Add – 1]

– 9 ≤ 3x < 9

– 3 ≤ x < 3 [Dividing by 3]

Hence, the solution set is {x : x ∈ R, – 3 ≤ x < 3}

Question-21.  Solve the following inequation and represent the solution set on the number line :

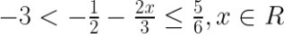
Answer:

(i) – 3 < – 1/2 – 2x/3

⇒ – 3 < (1/2 + 2x/3

⇒ – (1/2 + 2x/3) > – 3

⇒ – 2x/3 > – 3 + 1/2

⇒ – 2x/3 > -5/2

⇒ 2x/3 < 5/2

⇒ x < 5/2 × 3/2

⇒ x < 15/4

or

⇒ – (2x/3) ≤ 5/6 + 1/2

⇒ -2x/3 ≤ (5 + 3)/6

⇒ -2/3.x ≤ 8/6

⇒ 2/3.x ≥ -8/6

⇒ x ≥ – 8/6 ×3/2

⇒ x ≥ – 2

⇒ – 2 ≤ x …(ii)

From (i) and (ii),

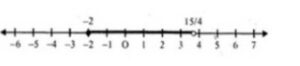
– 2 ≤ x ≤ 15/4

∴ Solution = {x : x ∈ R, – 2 ≤ x < 15/4}

Now solution on number line

Question -22. Solving the following inequation, write the solution set and represent it on the number line. – 3(x – 7)≥15 – 7x > (x+1)/3, n ∈R

Answer :

– 3(x – 7)≥15 – 7x > (x+1)/3, n ∈R

⇒ -3(x – 7) ≥ 15 – 7x ⇒ – 3x + 21 ≥ 15 – 7x

⇒ – 3x + 7x ≥ 15 – 21 ⇒ 4x ≥ – 6

⇒ x ≥ -6/4

⇒ x ≥ -3/2

⇒ -3/2 ≤ x

And 15 – 7x > (x + 1)/3

⇒ 45 – 21x > x + 1

⇒ 45 – 1 > x + 21x

⇒ 44 > 22x

2 > x ⇒ x = 2

∴ -3/2 ≤ x < 2, x ∈ R

Question -23. Solving the following inequation , write the solution set and represent it on the real number line. -2+10x ≤13x +10<24+10x, x ∈ Z.

Answer:

(a) Given that :

Question -24.  Solve the inequation 2x – 5 ≤ 5x + 4 < 11, where x ∈ I. Also represent the solution set on the number line. (2011)

Answer :

2x – 5 ≤ 5x + 4 < 11 2x – 5 ≤ 5x + 4
=> 2x – 5 – 4 ≤ 5x and 5x + 4 < 11
=> 2x – 9 ≤ 5x and 5x < 11 – 4
and 5x < 7
=> 2x – 5x ≤ 9 and x < 
=> 3x > – 9 and x< 1.4
=> x > – 3

Question-25. If x ∈ I, A is the solution set of 2 (x – 1) < 3 x – 1 and B is the solution set of 4x – 3 ≤ 8 + x, find A ∩B.

Answer:

2 (x – 1) < 3 x – 1
2x – 2 < 3x – 1
2x – 3x < – 1 + 2 => – x < 1 x > – 1
Solution set A = {0, 1, 2, 3, ..,.}
4x – 3 ≤ 8 + x
4x – x ≤ 8 + 3
=> 3x ≤ 11
=> x ≤ 11/3
Solution set B = {3, 2, 1, 0, – 1…}
A ∩ B = {0, 1, 2, 3} Ans.

Question -26. If P is the solution set of – 3x + 4 < 2x – 3, x ∈ N and Q is the solution set of 4x – 5 < 12, x ∈ W, find

(i) P ∩ Q
(ii) Q – P.

Answer:

(i) – 3 x + 4 < 2 x – 3

– 3x – 2x < – 3 – 4

=> – 5x < – 7

– x < – 7/5

⇒ x > 7/5

∴ Solution set P = {2, 3, 4, 5, …….}

4x – 5 < 12

4x < 12 + 5 ⇒ 4x < 17

x < 17/4

∵ x ∈ W

∴ Solution set Q = {4, 3, 2, 1, 0}

(i) P ∩ Q = {2, 3, 4}

(ii) Q – P = {1, 0}

Question -27. A = {x : 11x – 5 > 7x + 3, x ∈R} and B = {x : 18x – 9 ≥ 15 + 12x, x ∈R}
Find the range of set A ∩ B and represent it on a number line

Answer :

A = {x : 11x – 5 > 7x + 3, x ∈R}
B = {x : 18x – 9 ≥ 15 + 12x, x ∈R}
Now, A = 11x – 5 > 7x + 3
=> 11x – 7x > 3 + 5
=> 4x > 8
=>x > 2, x ∈ R

B = 18x – 9 ≥ 15 + 12x

⇒ 18x – 12x ≥ 15 + 9

⇒ 6x ≥ 24

⇒ x ≥ 4

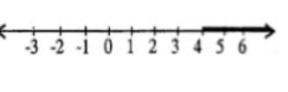
∴ A ∩ B = x ≥ 4, x ∈ R

Hence Range of A ∩ B = {x : x ≥ 4, x ∈ R} and its graph will be.

Question -28.

Given: P {x : 5 < 2x – 1 ≤ 11, x∈R)
Q{x : – 1 ≤ 3 + 4x < 23, x∈I) where
R = (real numbers), I = (integers)
Represent P and Q on number line. Write down the elements of P ∩ Q. (1996)

Answer :

P= {x : 5 < 2x – 1 ≤ 11}
5 < 2x – 1 ≤ 11

Question -29. If x ∈ I, find the smallest value of x which satisfies the inequation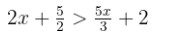

Answer :

=>
=>12x – 10x > 12 – 15
=> 2x > – 3
=> x > -3/2
Smallest value of x = – 1 Ans.

Question- 30. Given 20 – 5 x < 5 (x + 8), find the smallest value of x, when.

(i) x ∈ I
(ii) x ∈ W
(iii) x ∈ N.

Answer :

20 – 5 x < 5 (x + 8)
⇒ 20 – 5x < 5x + 40
⇒ – 5x – 5x < 40 – 20
⇒ – 10x < 20
⇒ – x < 2
⇒ x > – 2
(i) When x ∈ I, then smallest value = – 1.
(ii) When x ∈ W, then smallest value = 0.
(iii) When x ∈ N, then smallest value = 1. Ans.

Question- 31. Solve the following inequation and represent the solution set on the number line :

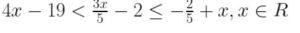
Answer :

We have

Hence, solution set is {x : -4 < x < 5, x ∈ R}
The solution set is represented on the number line as below.

⇒ 4x – 19 < 3x/5 – 2 and 3x/5 – 2 ≤ -2/5 + x, x ∈ R

⇒ 4x – 3x/5 < 17 and – 2 + 2/5 ≤ x – 3x/5, x ∈ R

⇒ 17x/5 < 17 and -8/5 ≤ 2x/5, x ∈ R

⇒ x < 5 and – 4 ≤ x, x ∈ R

⇒ – 4 ≤ x < 5, x ∈ R

Hence, solution set is {x : 4 ≤ x < 5, x ∈ R}

The solution set is represented on the number line as below.

Question- 32. Solve the given inequation and graph the solution on the number line :
2y – 3 < y + 1 ≤ 4y + 7; y ∈ R.

Answer :

2y – 3 < y + 1 ≤ 4y + 7; y ∈ R.
(a) 2y – 3 < y + 1
⇒ 2y – y < 1 + 3
⇒ y < 4
⇒ 4 > y ….(i)
(b) y + 1 ≤ 4y + 7

⇒ y – 4y ≤ 7 – 1

⇒ 3y ≤ 6

⇒ y ≤ 6/-3

⇒ y ≥ – 2 ….(ii)

From (i) and (ii),

4 > y ≥ – 2 or – 2 ≤ y < 4

Now representing it on a number given below

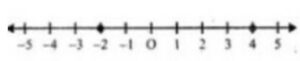
Question -33. Solve the inequation and represent the solution set on the number line.

Answer -33

Given :

Question -34. Find the greatest integer which is such that if 7 is added to its double, the resulting number becomes greater than three times the integer.

Answer :

Let the greatest integer = x
According to the condition,
2x + 7 > 3x
⇒ 2x – 3x > – 7
⇒ – x > – 7
⇒ x < 7
Value of x which is greatest = 6 Ans.

Question -35. One-third of a bamboo pole is buried in mud, one-sixth of it is in water and the part above the water is greater than or equal to 3 metres. Find the length of the shortest pole.

Answer :

Let the length of the shortest pole = x metre

Length of pole which is buried in mud = x/3

Length of pole which is in the water = x/6

According to this problem,

x – [x/3 + x/6] ≥ 3

⇒ x – (2x + x)/6 ≥ 3

⇒ x – x/2 ≥ 3

⇒ x/2 ≥ 3

⇒ x ≥ 6

∴ Length of pole (shortest in length) = 6 metres

— : End of ML Aggarwal Linear Inequation Exe-4 Class 10 ICSE Maths Solutions :–

Return to :- ML Aggarwal Solutions for ICSE Class-10

Thanks

Please Share with Your Friends