Loci Class 10 OP Malhotra Exe-13C ICSE Maths Solutions Ch-13. We Provide Step by Step Solutions / Answer of S Chand OP Malhotra Maths. In this article you would learn Howto solve problems on Constructions. Visit official Website CISCE for detail information about ICSE Board Class-10 Mathematics.
Loci Class 10 OP Malhotra Exe-13C ICSE Maths Solutions
| Board | ICSE |
| Publications | S Chand |
| Subject | Maths |
| Class | 10th |
| Chapter-13 | Loci |
| Writer | OP Malhotra |
| Exe-13C | Problems on Constructions |
| Edition | 2025-2026 |
Exercise- 13C
Loci Class 10 OP Malhotra Exe-13C ICSE Maths Solutions Ch-13
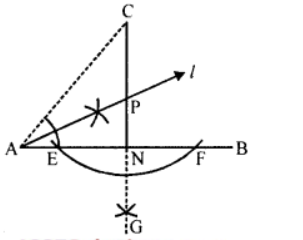
Que-1: Without using set-square or protractor, draw
(i) the perpendicular CN from C to AB;
(ii) the point P on CN equidistant from AB and AC.
Sol: (i) Steps of construction :
(a) Draw a line AB and take a point C out side it.
(b) From C, draw an arc with suitable radius which intersects. AB at E and F.
(c) With centres E and F, draw arcs intersecting each other at G.
(d) Join CG meeting AB at N.
Then CN ⊥ AB.
(e) Join CA.
(ii) Draw the angle bisector l.
∠CAB which intersects the perpendicular CN at P.
P is the required point equidistant from AB and AC.
Que-2: Without using set-squares or protractor, draw a triangle FGH in which GH = 2.5 units, FG = FH, and the altitude FX = 3 units. Measure FG.
Sol: Steps of construction :
(i) Draw a line segment GH = 2.5 units (cm).
(ii) Draw its perpendicular bisector l and cut off XF = 3 units (cm).
(iii) Join FG and FH.
On measuring FG, it is 3.4 units (cm).

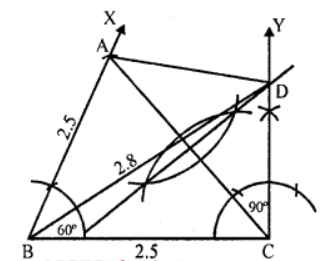
Que-3: Using ruler and compasses only, construct a quadrilateral ABCD in which AB = 2 units, BC = 2.5 units, ∠ABC = 60°, ∠BCD = 90° and AD = DC. Measure the length of BD.
Sol: Steps of Construction :
(i) Draw a line segment BC = 2.5 units.
(ii) At B, draw a ray making an angle of 60° and at C, a ray making an angle of 90°.
(iii) Cut off BA = 2 units.
(iv) Join AC and draw its perpendicular bisector which meets CY at D.
(v) Join AD.
(vi) Join BD, on measuring it, it is 2.8 units. Then ABCD is the required quadrilateral.
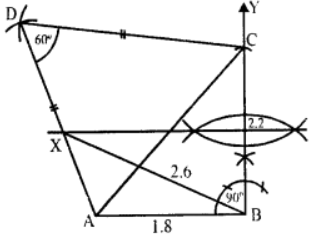
Que-4: Without using set square or protractor, construct a quadrilateral ABCD in which BC = 2.2 units, ∠ABC = 90°, AB = 1.8 units, AD = DC and ∠ADC = 60°. Construct also the perpendicular bisector of BC to meet AD at X and measure XB.
Sol: Steps of Construction :
(i) Draw a line segment AB = 1.8 units.
(ii) At B, draw a ray by making an angle of 90° and cut off BC = 2.2 units.
∵ ∠D = 60° and DA = DC
△ADC is an equilateral triangle.
(iii) With centre A and C and radius AC, draw arcs intersecting each other at D.
(iv) Join AD and CD.
(v) Draw the perpendicular bisector of BC which intersects AD at X.
(vi) Join BX.
On measuring, BX = 2.6 units.
Que-5: Draw a triangle ABC in which BC = 5.3 cm, the angle A = 38°, and the angle B = 56°. Using ruler and compasses only, construct the circle that passes through A, B and C.
Sol: Steps of Construction :
In △ABC, ∠B = 56°, ∠A = 38°
∴ ∠C = 180° – (∠B + ∠A)
= 180° – (56° + 38°)
= 180° – 94° = 86°
(i) Draw a line segment BC = 5.3 cm.
(ii) At B, draw a ray making an angle of 56° and at C, a ray making an angle of 86°. Which meet eachother at A.
(iii) Now draw the perpendicular bisectors of sides BC and CA which intersect eachother at O.
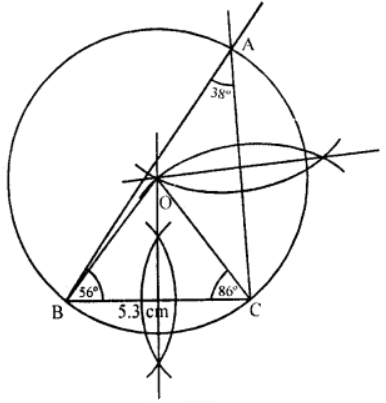
(iv) With centre O and radius OA or OB or OC, draw a circle which passes through A, B and C.
This is the required circle.
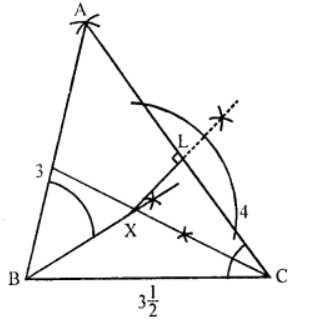
Que-6: Draw a triangle with sides 3 units, {3*(1/2)} units, and 4 units, without using setsquare or protractor, construct the bisector of two of the angles of the triangle and let them meet at the point X. Construct also the perpendicular XL from X to the longest side.
Sol: Steps of construction :
(i) Draw a line segment BC = {3*(1/2)} units.
(ii) With centre B and radius 3 units and with centre C and radius 4 units draw arcs intersecting each other at A.
(iii) Join AB and AC.
(iv) Draw the angle bisector of ∠B and ∠C intersecting each other at X.
(v) From X, draw a perpendicular XL on the longest side AC.
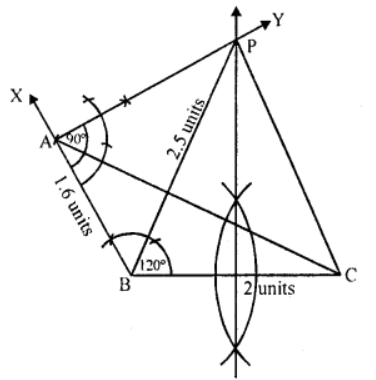
Que-7: Without using set-square or protractor, construct a triangle ABC in which AB = 1.6 units, BC = 2 units and ∠ABC = 120°. Find a point P outside the triangle such that ∠BAP = 90° and BP = CP. Measure the length of BP.
Sol: Steps of construction :
(i) Draw a line segment BC = 2 units.
(ii) Draw a ray BX at B making an angle of 120° and cut off BA =1.6 units.
(iii) Join AC.
(iv) At A, draw a ray AY making an angle of 90°.
(v) Draw the perpendicular bisector of BC which intersects AY at P.
P is the required point and join PB and PC on measuring PB, it is 2.5 units.
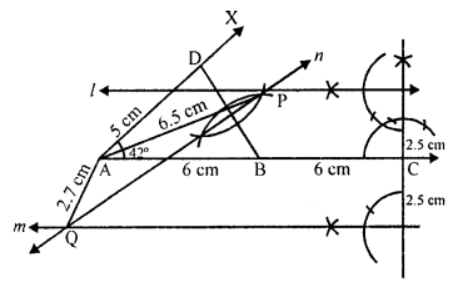
Que-8: Draw a line ABC making AB and BC each 6 cm long. At B draw BD of length 5 cm, making angle ABD = 42°. Find by construction two points P, Q each of which is equidistant from B and D and 2.5 cm from the line ABC. Measure PA and QA. (Use of set-square is permitted. No explanation or proof is required bat all construction lines must be clearly shown.)
Sol: Steps of construction :
(i) Draw a line segment AB such that AB =BC = 6 cm.
(ii) Draw a ray AX at A making an angle of 42° and cut off AD = 5 cm.
(iii) Join BD and draw its perpendicular bisector n.
(iv) Draw parallel lines l and m parallel to ABC at a distance of 2.5 cm from ABC. Which intersect the perpendicular bisector n at P and Q.
Then P and Q are the required points.
Now Join AP and AQ.
On measuring AP = 6.5 cm and AQ = 2.7 cm (approx)
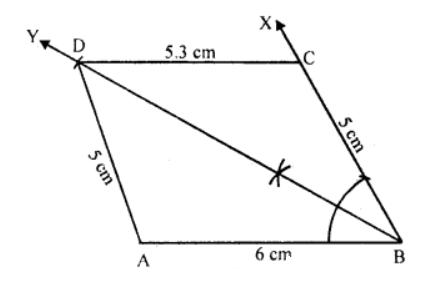
Que-9: Using ruler and compasses only, construct a quadrilateral ABCD in which AB = 6 cm, BC = 5 cm, ∠B = 60°, AD = 5 cm and D is equidistant from AB and BC. Measure CD.
Sol: Steps of construction :
(i) Draw a line segment AB = 6 cm.
(ii) At B, draw a ray BX making an angle of 60° and cut off BC = 5 cm.
(iii) Draw the angle bisector BY of ∠B.
(iv) With centre A and radius 5 cm. draw an arc which intersects BY at D.
(v) Join AD and CD.
ABCD is the required quadrilateral.
On measuring CD, it is 5.3 cm.
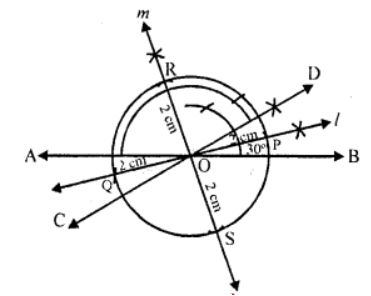
Que-10: Draw two intersecting lines to include an angle of 30°. Use ruler and compasses to locate points which are equidistant from these lines and also 2 cm away from their point of intersection. How many such points exist?
Sol: Steps of constuction :
(i) AB and CD are two intersecting lines making an angle of 30° at O.
(ii) Draw the angle bisector P of ∠BOD and produce it to other side also and also the bisector m ∠AOD.
(iii) With centre O and radius 2 cm, mark points P and Q on l. Similarly mark the points R and S on bisector m.
Then P, Q, R and S are four required points.
Que-11: Without using set square or protractor, construct rhombus ABCD with sides of length 4 cm and diagonal AC of length 5 cm. Measure ∠ABC. Find the point R on AD such that RB = RC. Measure the length of AR.
Sol: Steps of construction :
(i) Draw a line segment AC = 5 cm.
(ii) With centres A, and C and radius 4 cm, draw arcs intersecting each other at B and D.
(iii) Join AB, BC, CD and AD. ABCD is the required rhombus on measuring ∠ABC, it is 78°.
(iv) Draw the perpendicular bisector of BC which intersects AD at R.
Now AR = 1.2 cm.

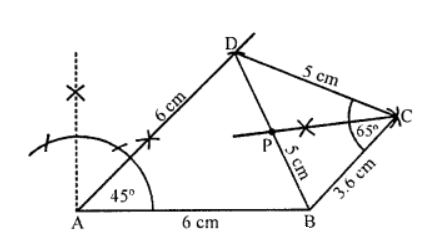
Que-12: Without using set square or protractor, construct a quadrilateral ABCD in which ∠BAD = 45°, AD = AB = 6 cm, BC = 3.6 cm and CD = 5 cm.
(i) Measure ∠BCD.
(ii) Locate the point P on BD which is equidistant from BC and CD.
Sol: Steps of construction :
(i) Draw a line segment AB = 6 cm.
(ii) At A, draw a ray making 45° and cut off AD = 6 cm.
(iii) With centre B and radius 3.6 cm and with centre D and radius 5 cm, draw arcs intersecting each other at C.
(iv) Join BC and CD.
ABCD is the required quadrilateral.
(v) On measuring ∠BCD, it is 65°.
(vi) Join BD.
(vii) Draw the bisector of ∠BCD which intersects BD at P.
P is the required point.
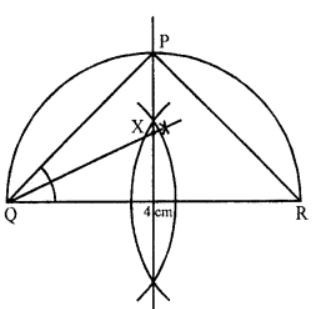
Que-13: By using ruler and compasses only, construct an isosceles triangle PQR in which QR = 4 cm, PQ = PR and ∠QPR = 90°. Locate the point X such that
(i) X is equidistant from the sides QR and PR.
(ii) X is equidistant from the points Q and R.
Sol: Steps of construction :
(i) Draw a line segment QR = 4 cm.
(ii) Draw a semicircle on QR as diameter.
(iii) Draw the perpendicular bisector of QR meeting the semicircle at P.
(iv) Join PQ and PR.
△PQR is the required isosceles triangle.
(v) Now draw the bisector of ∠Q which meets the perpendicular bisector of QR at X.
X is the required point which is equidistant from QR and PR and also from Q and R.
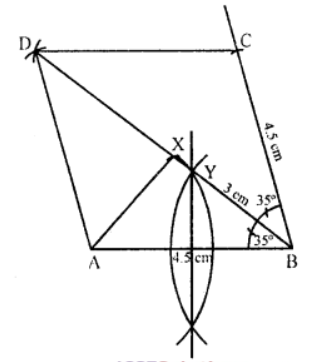
Que-14: Construct a triangle ABX such that AB = 4.5 cm and BX = 3 cm and ∠ABX = 35°. Complete the rhombus ABCD such that X is equidistant from AB and BC. Locate the point Y on the line BX such that Y is equidistant from A and B.
Sol: Steps of construction :
(i) Draw a line segment AB = 4.5 cm.
(ii) At B, draw a ray making an angle of 35° and cut off BX = 3 cm.
(iii) As X is equidistant from AB and BC.
∴ X will be on the angle bisector of ∠ABC.
(iv) Now draw BC such that ∠XBC = ∠ABX = 35°.
(v) Cut off BC = AB.
(vi) Now with centre C and A, and radius AB draw arcs intersecting each other at D.
(vii) Join CD and AD.
Then ABCD is the required rhombus.
(viii) Draw the perpendicular bisector of AB which meets BX at Y.
Y is the required point which is equidistant from A and B.
Que-15: Construct ∠AOB = 75°, Mark a point P equidistant from OA and OB such that its distance from another given line CD is 3 cm.
Sol: Steps of construction :
(i) Draw an angle AOB = 75° and a line CD.
(ii) Draw the angle bisector OE of ∠AOB.
(iii) Take a point L and draw a perpendicular and cut off LM = 3 cm:
(iv) Through M, draw a line P parallel to CD which intersects OE at P.
P is the required point.

–: End of Loci Class 10 OP Malhotra Exe-13C ICSE Maths Solutions Ch-13 :–
Return to : OP Malhotra S Chand Solutions for ICSE Class-10 Maths
Thanks
Please Share with Your Friend