Logarithms Class 9 OP Malhotra Exe-7C ICSE Maths Solutions

Logarithms Class 9 OP Malhotra Exe-7C ICSE Maths Solutions Ch-7. We Provide Step by Step Solutions / Answer of Complex Problems on Logarithms. Visit official Website CISCE for detail information about ICSE Board Class-9 Mathematics.

Logarithms Class 9 OP Malhotra Exe-7C ICSE Maths Solutions Ch-7

Board	ICSE
Publications	S Chand
Subject	Maths
Class	9th
Chapter-7	Indices Exponents
Writer	OP Malhotra
Exe-7C	Complex Problems on Logarithms  with Answer
Edition	2025-2026

Complex Problems on Logarithms  with Answer

Logarithms Class 9 OP Malhotra Exe-7C ICSE Maths Solutions Ch-7.

Find the value of the following :

Que-1: log 6

Sol: log 6 = log (2 x 3)
= log 2 + log 3
= 0.3010 + 0.4771
= 0.7781

Que-2: log 12

Sol: log 12 = log (2 x 2 x 3)
= log (2² x 3)
= log 2² + log 3
= 2 log 2 + log 3
= 2 (0.3010) + 0.4771
= 0.6020 + 0.4771
= 1.0791

Que-3: log 15

Sol: log 15 = log (3 x 5)
= log 3 + log 5
= 0.4771 + 0.6990
= 1.1761

Que-4: log 200

Sol: log 200 = log (2³ x 5²)
= log 2³ + log 5²
= 3 log 2 + 2 log 5
= 3 (0.3010) + 0.6990 x 2
= 0.9030 + 1.3980
= 2.3010

Que-5: log 36

Sol: Log 36 – log (4 x 9) = log (2² x 3²)
= log 2² + log 3²
= 2 log 2 + 2 log 3
= 2 (0.3010) + 2 (0.4771)
= 0.6020 + 0.9542
= 1.5562

Que-6: log 80

Sol: log 80 = log (2⁴ x 5)
= log 2⁴ + log 5
= 4 log 2 + log 5
= 4 (0.3010) + 0.6990
= 1.2040 + 0.6990
= 1.9030

Que-7: log 2*(1/3)

Sol: log {2*(1/3)} = log(7/3)
= log 7 – log 3
= 0.8451 – 0.4771
= 0.3680

Que-8: log 11³

Sol: log (11)³
= 3 log 11
= 3 x 1.0414
= 3.1242

Que-9: log {2*(1/3)}^5

Sol: log {2*(1/3)}^5 = log (7/3)^5
= 5 log (7/3)
= 5 [log 7 – log 3]
= 5 [0.8451 – 0.4771]
= 5 (0.3680) = 1.8400

Que-10: If log 6 = 0.7782, find the value of log 36.

Sol: log 6 = 0.7782
log 36 = log (6)²
= 2 log 6
= 2 (0.7782)
= 1.5564

Que-11: Given log₁₀ 25 = x, log₁₀ 75 = y, evaluate without using logarithmic tables, in terms of x and y.
(i) log₁₀ 3
(ii) log₁₀2

Sol: (i) log₁₀ 3
= (log10) (75/25)
= (log10 75) – (log10 25)
= y – x

(ii) log₁₀2 = x
= log 5² = x
= 2 log 5 = x
= log 5 = x/2
= (log10) 2 = log (10/5)
= (log 10) – (log 5)
= 1 – (x/2)
= (2-x)/2

Que-12: Given log 31.87 = x, write down in terms of x.
(i) log (31.87)²
(ii) log₁₀ 0.03187
(iii) log₁₀ √31870

Sol: log 31.87 = x
(i) log (31.87)² = 2 log (31.87)
= 2x

(ii) log10 0.03187 = log10 (31.87)/(1000)
= log10 31.87 – log10 1000
= x – 3 (log 1000 = 3)

(iii) log10 √31870 = log10 (31870)^1/2
= (1/2) log10 31870
= (1/2) log (31.87 x 1000)
= (1/2) [log 31.87 + log 1000]
= (1/2) (x + 3) = (x+3)/2

Que-13: Solve the equation
(i) log₁₀ (x + 1) + log₁₀ (A – 1) = log₁₀ 11 + 2 log₁₀3
(ii) log (10x + 5) – log (x – 4) = 2

Sol: (i) log₁₀ (x + 1) + log₁₀ (A – 1) = log₁₀ 11 + 2 log₁₀3
⇒ log (x + 1) (x – 1) = log (11 x 3²) (∵ 2 log₁₀ 3 = log₁₀ 3²)
⇒ log (x² – 1) = log (11 x 9) ⇒ log (x² – 1) = log 99
Comparing we get.
x² – 1 = 99
⇒ x² = 99 + 1
= 100 = (10)²
⇒ x = 10
∴ x = 10

(ii) log (10x + 5) – log (x – 4) = 2
⇒ log (10x+5)/(x−4) = log 100 (∵ log 100 = 2)
Comparing both sides,
(10x+5)/(x−4) = 100/1
100x – 400 = 10x + 5
⇒ 100x – 10x = 5 + 400
⇒ 90x = 405
⇒ x = 405/90 = 45/10 = 4.5
∴ x = 4.5

Que-14: (a) Given 2 log₁₀x + (1/2) log₁₀y = 1, express y in terms of x.
(b) Express as a single logarithm :
2 log 3 – (1/2) log 16 + log 12

Sol:  (a) Given 2 log₁₀x + (1/2) log₁₀y = 1
{(log10) x²} + {(log10) y^(1/2)} = log10 10
= {(log10) x²} × y^(1/2) = log10 10
Comparing,
= x² . y^(1/2) = 10
= y^(1/2) = 10/x²
Squaring, y = (10/x²)²
= 100/x^4 = 100x^-4
y = 100x^-4.

(b) 2 log 3 – (1/2) log 16 + log 12
= log 3² – log 16^(1/2) + log 12
= log {3²×12}/(16^(1/2))
= log {(9×12)/4}
= log 27.

Que-15: Given that log₁₀ y + 2log₁₀ x = 2, express y in terms of x.

Sol: log10 y + 2 log10 x = 2
log10 y + log10 x² = log 10^2
log (y × x²) = log 100
y × x² = 100
y = ( 100 / x )²

Que-16: If a = 1 + log₁₀ 2 – log₁₀ 5, b = 2 log10 3 and c = log₁₀ m – log₁₀ 5, find the value of m if a + b = 2c (Do not use log tables).

Sol: a = 1 + log10 2 – log10 5 = log10 10 + log10 2 – log10 5
= log10 (10×2)/5 = log10 4
b = 2 log10 3 = log10 3² = log10 9
c = log10 m – log10 5 = log10 (m/5)
∵ a + b = 2c
∴ log10 4 + log10 9 = 2 log (m/5)
⇒ log (4 × 9) = log (m/5)² = log m²/25
Comparing both sides,
4 x 9 = m²/25
⇒ m² = 4 x 9 x 25
= 900 = (30)²
∴ m = 30

Que-17: Express as a single logarithm
2 + (1/2) log10 9 – 2 log10 5

Sol: 2 + (1/2)log10 9 – 2log10 5
= 2 +(1/2)log10 3² – 2log10 5
= 2log10 + (1/2) × 2log10 3 – 2log10 5
= log 10² + log10 3 – log10 5²
= log 100 + log10 3 – log10 25
= log10 {(100×3)/25}
= log10 12.

Que-18: If a = log 12, b – log 6 and c = 2 log √2, find
(i) a – b – c
(ii) 9^a-b-c

Sol:  a = log 12, b = log 6, c = 2 log √2 = log
(√2)² = log 2
(i) a – b – c = log 12 – log 6 – log 2
= log {12/(6×2)}
= log 1 = 0 (∵ log 1 = 0)

(ii) 9^a-b-c = 9° [∵ a – b – c = 0 proved in (i)]
= 1 (∵ x° = 1)

Que-19: If x = log₁₀ 12, y = log₄ 2 x log₁₀ 9 and z = log₁₀ (0.4) then find
(i) x – y – z
(ii) prove that 6^{x – y- z} = 6

Sol: x = log₁₀ 12, y = log₄ 2 x log₁₀ 9, z = log₁₀ (0.4)
(i) x = log₁₀ 12 = log₁₀ (2² x 3) = log 2² + log 3
= 2 log₁₀ 2 + log₁₀ 3
y = log₄ 2 x log₁₀9 = log₄2 x log₁₀ 3²
= log₄ 2 x 2 log₁₀ 3 = log₄ (4)^(1/2) x = log₁₀ 12, y = log₄ 2 x log₁₀ 9, z = log₁₀ (0.4)
(i) x = log₁₀ 12 = log₁₀ (2² x 3) = log 2² + log 3
= 2 log₁₀ 2 + log₁₀ 3
y = log₄ 2 x log₁₀9 = log₄2 x log₁₀ 3²
= log₄ 2 x 2 log₁₀ 3 = log₄ (4) (4/10) = log₁₀ 4 – log₁₀ 10
= log₁₀ 2² – 1 = 2 log₁₀ 2 – 1
x – y – z = 2 log₁₀ 2 + log₁₀ 3 – log₁₀ 3 – 2 log₁₀2 + 1 = 1

(ii) 6^x-y-z = 6¹ = 6 [∵ x – y – z = 1 (proved in (i)]
Hence proved.

Que-20: If p = log₁₀ 20 and q = log₁₀ 25, find x such that 2 log₁₀ (x + 1) = 2p – q.

Sol: p = log₁₀ 20 = log₁₀ (22 x 5) = log₁₀ 2² + log₁₀ 5
= 2 log 2 + log 5
q = log₁₀ 25 = log₁₀ (5²) = 2 log₁₀ 5
Now,
2p – q = 2 [2 log₁₀ 2 + log₁₀ 5] – 2 log₁₀ 5
= 4 log₁₀ 2 + 2 log₁₀ 5 – 2 log₁₀ 5
= 4 log₁₀ 2 = 2 log₁₀ 2²
= 2 log₁₀ 4
2 log₁₀(x + 1) = 2 log₁₀ 4
Comparing, we get
x + 1 = 4 ⇒ x = 4 – 1 = 3
∴ x = 3

Que-21: Without using logarithm tables, evaluate :
3 + log₁₀ (10^-2)

Sol: 3 + log₁₀ (10^-2) = 3 + (- 2 log₁₀ 10)
= 3 – 2 log₁₀ 10 = 3 – 2 x 1
= 3 – 2 = 1 (∵ log_a a = 1)
= 1

Que-22: Given log₁₀ x = a, log₁₀ y = b
(i) Write down 10^n-1 in terms of x
(ii) Write down 10^2b in terms of y
(iii) If log₁₀ P = 2a – b, express P in terms of x and y.

Sol: (i) log₁₀ x = a, log₁₀y = b
∵ log₁₀ x = a and log₁₀ y = b
∴ 10ⁿ = x … (i)
∴ 10^b = y … (ii)
Now,
(i) 10^n-1 = (10^a)/(10¹) = x/10 [From (i)]
(ii) 10^2b = (10^b)² = y² [From (ii)]
(iii) log₁₀ P = 2a – b
⇒ log₁₀P = 2 log₁₀x – log₁₀y
⇒ log₁₀ P = log x² – log₁₀ y
⇒ log₁₀ P = log x²/y
Comparing, we get
p = x²/y

Que-23: Simplify without using tables :
2log10 5 + log10 8 − (1/2)log10 4

Sol: 2log10 5 + log10 8 − (1/2)log10 4
= log10 5² + log10 8 – log10 (4)^(1/2)
= log 10 25 + log 8 – log10 2
= log10 {25×8}/2
= log10 100 = 2

Que-24: Given that log₁₀2 = x, log₁₀ 3 = y, find
(i) log₁₀ 60
(ii) log₁₀1.2 in terms of x and y

Sol: (i) log10 60 = log10 (2 x 3 x 10)
= log10 2 + log10 3 + log10 10
= x + y + 1 (∵ log10 10 = 1)

(ii) log10 1.2 = log10 (12/10) = log10 12 – log10 10
= log (2² x 3) – log10 10
= 2 log 2 + log 3 – log10 10 (∵ log10 10 = 1)
= 2x + y – 1

Que-25: Given 2 log₁₀ x + 1 = log₁₀ 250, find
(i) x
(ii) log₁₀2x

Sol: (i) 2 log₁₀ x + 1 = log 250
⇒ log₁₀x² + 1 = log₁₀ 250
⇒ log₁₀ x² + log₁₀ 10 = log₁₀ 250 (∵ log_a a = 1)
⇒ log (x² x 10) = log₁₀ 250
Comparing both side,
10x² = 250
⇒ x² = 25 = (5)²
∴ x = 5

(ii) log₁₀ 2x = log₁₀ 2 x 5
= log₁₀ 10 = 1

Que-26: (a) Given that log x = m + n and log y = m – n, express the value of log₁₀ (10x/y) in terms of in and n. (b) Solve for x : log₁₀x = – 2.

Sol: (a) log x = m + n, log y = m – n
log10 10x/y² = {log10 10x} − {log10 y²}
= log10 10 + log10 x – 2 log10 y
= 1 + m + n – 2 (m – n)
= 1 + m + n – 2m + 2n
= 1 – m + 3n

(b) log10 x = – 2 = log10 1/100
Comparing we get,
x = 1/100

Que-27: If log {(p+q)/3} = 1/2 = (log p + log q) prove that p² + q² = 7pq.

Sol: Log ((p+q)/3) = 1/2 = (log p + log q)
⇒ log (p+q)/3 = 1/2 (log p×q) = log(pq)^(1/2)
Comparing we get,
(p+q)/3 = (pq)^(1/2)
Squaring both sides,
{(p+q)/3}² = pq
⇒ {p² + q² + 2pq}/9 = pq
⇒ P² + q² + 2 pq
⇒ p² + q² + 2pq = 9pq
⇒ p² + q² = 9pq – 2pq ⇒ 7pq
∴ p² + q² = 2pq
Hence proved.

Que-28: If x² + y² = 51xy, prove that log 1/2 = 1/2 (log x + log y).

Sol: x² + y² = 51xy
⇒ x² + y² – 2xy = 51 xy – 2xy
(Subtracting 2xy)
⇒ (x – y)² = 49xy
= {(x-y)²/49} = xy
= {(x-y)²/7²} = xy
= {(x-y)/7}² = xy
= {(x-y)/7} = √xy
Taking log on both sides,

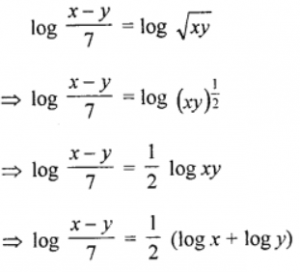
Hence, Proved.

— : End of Logarithms Class 9 OP Malhotra Exe-7C ICSE Maths Ch-7 Step by Step Solutions :–

Return to :–  OP Malhotra S Chand Solutions for ICSE Class-9 Maths

Thanks

Please Share with Your Friends