Magnetic Flux and Faraday’s Laws Numerical Class-12 Nootan ISC Physics Solution Ch-11 Electromagnetic Induction. Step by step solutions of Kumar and Mittal Physics of Nageen Prakashan as council latest prescribe guideline for upcoming exam. Visit official Website CISCE for detail information about ISC Board Class-12 Physics.
Magnetic Flux and Faraday’s Laws Numerical Class-12 Nootan ISC Physics Solution Ch-11 Electromagnetic Induction
| Board | ISC |
| Class | 12 |
| Subject | Physics |
| Book | Nootan |
| Chapter-11 | Electromagnetic Induction. |
| Topics | Numericals on Magnetic Flux and Faraday’s Laws |
| Academic Session | 2025-2026 |
Numericals on Magnetic Flux and Faraday’s Laws
Class-12 Nootan ISC Physics Solution Ch-11 Electromagnetic Induction.
Que-1: The area enclosed by a circular coil of 2000 turns is 10 cm². Its plane is kept perpendicular to a magnetic field of 0.3 Wb m^- 2 and is rotated through 180°. Calculate the change in magnetic flux.
Ans- φ1 = NBA
=> 2000 x 0.3 x 10 x 10^-4 = 0.6 weber
φ2 – NBAcos180° = -0.6 weber
∴IΔφI = I-0.6-0.6I = 1.2 weber
Que-2: The magnetic flux through a coil of 50 turns changes from 0.3 Wb to zero in 1 second. Calculate the induced emf across the two ends of the coil.
Ans- φ1 = 50 x 0.3 = 15 weber
φ2 = 0
Δφ = 0 – 15 = -15 weber
e = -Δd/Δt = -(-15)/1 = 15 volt
Que-3: A coil of area 0.5 m²and having 100 turns is placed 2 perpendicular to a magnetic field of 0.04 Wb m^- 2 If the coil is suddenly removed away from the field in 0.01 second, calculate the average emf induced in the coil.
Ans- φ1 = 100 x 0.5 x 0.04 = 2
φ2 = 0
emf = -Δd/Δt = 0-2/0.01 = 200 volt
Que-4: A coil of area 0.15m^2 and 50 turns is normal to a magnetic field which changes from 5 x 10^-3 to 2 x 10^-3 x Wb m^-2 in 30 ms. Compute the emf induced in the coil.
Ans- φ1 = 50 x 1.5 x 5 x 10^-3
φ2 = 50 x 1.5 x 2 x 10^-3
Δd = d2 – d1
=> 50 x 1.5 x 10^-3 (2-5)
=> 50 x 1.5 x 10^-3 x 3
∴e = -Δd/Δt = 50 x 1.5 x 10^-3 x 3 / 30 x 10^-3 = 0.75 volt
Que-5: A ring of radius 10 cm and resistance 2 Ω is placed in a uniform magnetic field which is perpendicular to the plane of ring. If the magnetic field is decreasing at the rate of 0.1 T s^-1 find the values of induced emf and induced current in the ring.
Ans- e = -dφ/dt
=> e = – d B.A / dt
=> e = A.(-dB/dt)
=> e = π x (10 x 10^-2)² (-(-0.1))
=> e = 3.14 x 10^-3 volt = 3.14 mV
∴ i = V/R = 3.14/2 = 1.57 mA
Que-6: A 28 turn coil with average diameter of 0.02 m is placed perpendicular to a magnetic field of 8000 T. If the field changes to 3000 T in 4 s, what is the magnitude of the induced emf? (pi = 22/7)
Ans- φ1 = 28 x 3.14 x (0.1)² x 8000 = 70.336 Wb
φ2 = 28 x 3.14 x (0.1)² x 3000 = 26.376
Δφ = φ2-φ1 = -43.96
now e = – Δφ/Δt = 43.96/4 ≈ 11 Volt
Que-7: A closed copper coil of area 1.0 m^2 placed perpendicular to a magnetic field of 0.10 T is rotated through 180° in 0.01 s. Find the induced emf and induced current in the coil whose resistance is 2.0 Ω. If the coil is open somewhere, then what will be the emf and the current?
Ans- φ1 = BAcos0 = 0.1 x 1 = 0.1 Wb
φ2 = BAcos180 = -0.1 Wb
Δφ = -0.2 Wb
e = Δφ/Δt = 0.2/0.01 = 20 V
i = e/R = 20/2 = 10 A
Que-8: A coil of area 500 cm^2 and 2000 turns is kept normal to a magnetic field of 4 x 10^5 Wb m^-2. It is rotated through 180° in 0.1 s. (i) Calculate the average induced emf. (ii) If the total resistance of the circuit be 20 Ω, calculate the induced charge.
Ans-
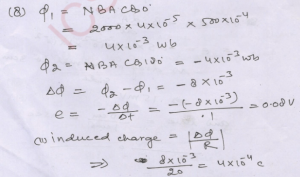
Que-9: A rectangular loop of sides 10 cm x 3 cm with a small cut is moving out of a uniform magnetic field of 0.5 T directed normal to the loop. Compute the voltage induced, across the cut, if the velocity of the loop is 1 cm s^-1 in a direction (i) normal to the longer side, (ii) normal to the shorter side of the loop. For how long does the induced voltage last in each case?
Ans-
(ii) e = -B . dA/dt
=> e = -0.5 x -3 x 10^-2 x 1 x 10^-2
as drag in normal to 3 cm side
=> 1.5 mV
and time = 10/1 = 10 sec
Que-10: A long solenoid of radius 0.01 m has 600 turns per metre. A smaller coil of 100 turns is wrapped closely around the centre of the bigger solenoid. If the current in the solenoid rises from zero to 2 A in 1 ms, find the emf induced in the smaller coil.
Ans- e = μ0nNA.di/dt
=> 4π x 600 x 100 x π x (0.1)² x 2 / 1 x 10^-3
=> 47.3 x 10^-3 V
=> 47.3 mV
Que-11: A small loop of area 2.0 cm^2 is placed inside a long solenoid having 1500 turns per metre, normal to the axis of the solenoid. Find the voltage induced in the loop while the current in the solenoid is changed from 2 A to 4 A in 0.1 s.
Ans- e = μ0nNA.di/dt {N=1}
=> 4π x 10^-7 x 1500 x 1 x 2 x 10^-4 x (4-2/0.1)
=> 7.5 x 10^-6 volt
— : End of Magnetic Flux and Faraday’s Laws Numerical Class-12 Nootan ISC Physics Solution Ch-11 Electromagnetic Induction. :–
Return to : – Nootan Solutions for ISC Class-12 Physics
Thanks
Please share with your friends



