Mathematical Induction Class 11 OP Malhotra Exe-8A ISC Maths Solutions

Mathematical Induction Class 11 OP Malhotra Exe-8A ISC Maths Solutions Ch-8 Solutions. In this article you would learn about Method and Proof of Mathematical Induction. Step by step solutions of latest textbook has been given as latest syllabus. Visit official Website CISCE for detail information about ISC Board Class-11 Mathematics.

Mathematical Induction Class 11 OP Malhotra Exe-8A ISC Maths Solutions Ch-8

Board	ISC
Publications	S Chand
Subject	Maths
Class	11th
Chapter-8	Mathematical Induction
Writer	O.P. Malhotra
Exe-8(A)	Method and Proof of Mathematical Induction.

Exercise- 8A

Mathematical Induction Class 11 OP Malhotra Exe-8A Solution.

Use the principle of mathematical induction to prove the following statements for all n ∈ N.

Que-1: 1 + 2 + 3 + … + n = (1/2) n(n + 1).

Sol: Let T (n) be the statement: 1 + 2 + 3 + … + n = (1/2) (n +1)
For n = 1 ; 1 = (1/2) x 1 (1 +1) which is true. ∴ T (1) is true.
Now let us assume that T (k) is true
i.e. 1 + 2 + 3 + … + k = (1/2) k (k +1)
Now, we shall prove that T (k + 1) is true.
Now, 1 + 2 + 3 + … + k + k + 1 = (1/2) k (k + 1) + k + 1 [using (1)]
= k+(1/2)[k + 2] = (1/2)(k + 1)(k + 1 + 1)
∴ T(k + 1) is true.
Hence by mathematical induction T (n) is true for all n ∈ N.

Que-2: 2 + 4 + 6 +… + 2n = n (n + 1).

Sol:  For n = 1 ; 2 = 1 (1 + 1)
∴ result is true for n = 1
Let us assume that result is true for n = m
i.e. 2 + 4 + 6 + … + 2m = m (m + 1) … (1)
We shall prove the result for n = m + 1
i.e. we want to prove that
2 + 4 + 6 + …. + 2 (m – 1) = (m + 1) (m + 2)
Now 2 + 4 + 6 + …. + 2m + 2 {m + 1) = m (m + 1) + 2 (m + 1) [using eqn. (1)]
= (m + 1) (m + 2)
= (m + 1) (m + 1 + 1)
∴ result is true for n = m + 1
Hence by mathematical induction result is true for all n ∈ N.

Que-3: 1² + 2² + 3² +…+ n² = (1/6) n (n + 1) (2n + 1).

Sol: For n = 1 ; 1² = (1/6) 1 (1 + 1) (2.1 + 1) = 6/6 = 1
∴ result is true for n = 1
Let us assume that result is true for n = m
∴ 1² + 2² + 3² + …. + m² = (1/6) m.(m + 1)(2m + 1) … (1)
We shall prove the result for n = m + 1

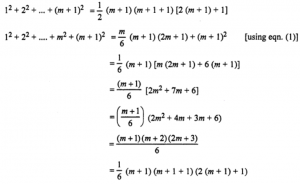
∴ result is true for n = m + 1
Hence by principle of mathematical induction result is true for all n ∈ N.

Que-4: 1² + 3² + 5² +… + (2n – 1)² = (1/3) n (2n – 1) (2n + 1)

Sol: Let P (n) be the statement:
1² + 3² + 5² + … + (2n – 1)² = (1/3) n (2n – 1) (2n + 1)
For n = 1 ; 1² = (1/3) x 1 (2 – 1)(2 + 1) = 1
∴ P (1) is true
Let us assume that P (m) is true, where m ∈ N
i.e. 1² + 3² + 5² …. + (2m – 1)² = (1/3) m(2m – 1)(2m + 1) … (1)
Now we shall prove that P (m + 1) is true.
Now P (m + 1): 1² + 3² + 5² … + (2m – 1)² + (2m + 1)²
= (m/3) (2m – 1) (2m + 1) + (2m + 1)² [using (1)]
= {(2m+1)/3} [m (2m – 1) + 3 (2m +1)] = (1/3) (2m + 1) (2m² + 5m + 3)
= (1/3) (2m + 1) (m + 1) (2m + 3) = (1/3) (m + 1) (2 (m + 1) – 1) (2(m + 1) + 1)
Thus P (m + 1) is true
Hence by mathematical induction result is true for all n ∈ N.

Que-5: 2 + 2² + 2³ + … + 2ⁿ = 2 (2n – 1).

Sol: Let P (n) be the given statement: 2 + 2² + 2³ + … + 2ⁿ = 2 (2ⁿ – 1)
For n = 1 ; 2 = 2 (2¹ – 1) = 2 x 1 = 2 ∴ P(1) is true
Let us assume that P (m) is true, where m ∈ N
i.e. 2 + 2² + 2³ + … + 2^m = 2 (2^m – 1) … (1)
We shall prove that P (m + 1) is true.
Now P (m + 1): 2 + 2² + 2³ + … + 2^m + 2^m+1
= (2 + 2² + 2³ … + 2^m) + 2^m+1
= 2(2^m – 1) + 2^m+1 [using eqn. (1)]
= 2^m+1 – 2 + 2^m+1 = 2 . 2^m+1 – 2
= 2 (2^m+1 – 1)
Thus P (m + 1) is true.
Hence by mathematical induction, P (n) is true for all n ∈ N

Que-6: 1.2 + 2.3 + 3.4 + … + n (n + 1) = {n(n+1)(n+2)}/3

Sol: Let P (n) be the statement:
1.2 + 2.3 + 3.4 + … + n (n + 1) = {n(n+1)(n+2)}/3
For n = 1 ; 1.2 = {1(1+1)(1+2)}/3 = 2 ∴ P (1) is true.
Let us assume that P (n) is true for n = m ∈ N
i.e. 1.2 + 2.3 + … + m (m + 1) = {m(m+1)(m+2)}/3 … (1)
We shall prove that P (m+ 1) is true.
Now P (m + 1): 1.2 + 2.3 + 3.4 + … + m (m + 1) + (m + 1) (m + 2)
= [1.2 + 2.3 + … + m (m + 1)] + (m + 1) (m + 2)
= {m(m+1)(m+2)}/3 + (m + 1) (m + 2) [using eqn. (1)]
= {(m+1)(m+2)(m+3)}/3 = [(m+1)(m+1+1)(m+1+2)]/3
∴ P(m + 1) is true.
Hence by mathematical induction result P (n) is true for all n ∈ N.

Que-7: 1.2 + 2.2² + 3.2³ +… + n.2ⁿ = (n – 1) 2ⁿ⁺¹ + 2.

Sol: Let P (n) be the statement : 1.2 + 2.2² + … + n.2ⁿ = (n – 1) 2ⁿ⁺¹ + 2
For n = 1 : 1.2 = (1 – 1)2¹⁺¹ + 2 = 2 ∴ P(1) is true.
Let us assume that P (m) is true where m ∈ N
i.e. 1.2 + 2.2² + 3.2² + … m . 2^m = (m – 1) 2^m+1 + 2 …(1)
Now we shall prove that P (m + 1) is true
Now P (m + 1) : 1.2 + 2.2² + 3.2² + …. + m.2^m + (m + 1) 2^m+1
= (1.2 + 2.2² + 3.2³ + … + m.2^m) + (m + 1) 2^m+1
= (m – 1) 2^m+1 + 2 + (m + 1) 2^m+1 [using (1)]
= (m – 1 + m + 1). 2^m+1 + 2 = 2m. 2^m+1 + 2 = (m + 1 – 1) 2^m+2 + 2
∴ P (m + 1) is true.
Hence by principle of mathematical induction P (n) is true or all n ∈ N.

Que-8: 3.2² + 3².2³ + 3³.2⁴ + … + 3ⁿ . 2ⁿ⁺¹ = (12/5)(6ⁿ – 1)

Sol: Let P (n) be the statement: 3.2² + 3².2³ + 3³.24 + … + 3n . 2n+1 = (12/5)(6n – 1)
For n = 1 ; 3.2² = (12/5) (61 – 1) = 12
∴ P (1) is true.
Let us assume that P (m) is true.
i.e. 3.2 + 3².2³ + … + 3m . 2m+1 = (12/5) (6m – 1) … (1)
Now we shall prove that P (m + 1) is true.

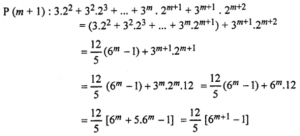
∴ P (m + 1) is true.
Hence by mathematical induction P (n) is true for all n ∈ N.

Que-9: 1.3 + 3.5 + 5.7 +… + (2n – 1) (2n + 1) = [{n(4n²+6n-1)}/3]

Sol: Let P (n) be the statement: 1.3 + 3.5 + 5.7 + … + (2n – 1) (2n + 1) = [{n(4n²+6n−1)}/3]
For n = 1; 1.3 = [1⋅(4⋅1²+6⋅1−1)]/3 = 3 ∴ P(1) is true
Let us assume that P (m) is true, where m ∈ N
i.e 1.3 + 3.4 + … + (2m – 1) (2m + 1) = [m(4m²+6m−1)]/3
Now we shall prove that P (m + 1) is true.

∴ P (m + 1) is true
Hence by mathematical induction P (n) is true for all n ∈ N.

Que-10: (i) a + (a + d) + (a + 2d) +… + [a + (n -1) d] = (n/2) [2a + (n – 1) d]
(ii) a + ar + ar² +… + ar^(n-1) = [a(1−r^n)]/(1−r), r ≠ 1.

Sol: (i) Let P (n) be the statement: a + (a + d) + (a + 2d) + … + [a + (n – 1) d] = (n/2) [2a + (n – 1)d]

For n = 1 ; a = (1/2) [2a + (1 – 1)d] = a ∴ P (1) is true.
Let us assume that P (m) is true where m ∈ N
i.e. a + (a + d) (a + 2d) + …. + [a + (m – 1) d] = (m/2) [2a + (m – 1) d] …(1)
Now, we shall prove that ∴ P (m + 1) is true.
Now P (m + 1) ; a + (a + d) + (a + 2d) + … + [a + (m – 1) d] + [a + (m + 1 – 1) d]
= a + (a + d)(a + 2d) + … + [a + (m – 1) d] + (a + md)
= (m/2) [2a + (m – 1)d] + (a + md) [using eqn. (1)]
= (ma + a) + (md/2) [(m – 1) + 2]
= (m + 1)a + (m/2) (m + 1)
= {(m+1)/2} [2a + (m + 1 – 1)d]
∴ P (m + 1) is true.
Hence by mathematical induction P (n) is true for all n ∈ N.

(ii) Let P (n) be the statement: a + ar + ar² + … + ar^(n-1) = {a(1−r^n)}}/(1−r) ; r≠1

For n = 1 ; a = {a(1−r^1)}/(1−r) = a ∴ P (1) is true.
Let us assume that P (m) is true where m ∈ N

∴ P (m + 1) is true
Hence by mathematical induction P (n) is true for all n ∈ N.

Que-11: 5 + 15 + 45 + … + 5 (3)^n-1 = (5/2) (3ⁿ – 1).

Sol: Let P (n) be the statement: 5 + 15 + 45 + … + 5 (3)^(n-1) = (5/2) ((3^n) – 1)
For n = 1 ; 5 = (5/2) (3¹ – 1) ∴ P(1) is true
Let us assume that P (m) is true where m ∈ N
i.e. 5 + 15 + 45 + … + 5 . 3^(m-1) = (5/2) ((3^m) – 1) …(1)
We shall prove that ∴ P (m + 1) is true.
Now P (m + 1): 5 + 15 + 45 + … + 5 . 3^(m-1) + 5 . 3^(m+1-1)
= [5 + 15 + 45 + …. + 5 . 3^(m-1)] + 5.3^m
= (5/2) ((3^m) – 1) + 5 . 3^m [using eqn. (1)]
= (5/2)[(3^m)−1+2⋅3^m] = (5/2) [3⋅(3^m)−1] = (5/2) [(3^(m+1)−1]
∴ P (m + 1) is true.
Hence by mathematical induction P (n) is true for all n ∈ N.

Que-12: (1/3.5) + (1/5.7) + (1/7.9) + … + [1/{(2n+1)(2n+3)}] = n/3(2n+3)

Sol: Let P(n) be the statement : (1/3.5) + (1/5.7) + (1/7.9) + … + [1/{(2n+1)(2n+3)}] = n/3(2n+3)
For n = 1 ; 1/3.5 = 1/{3(2.1+3)}
= 1/15 ∴ P (1) is true.

Que-13: (1/1.4) + (1/4.7) + (1/7.10) + … + [1/{(3n−2)(3n+1)}] = n/3n+1.

Sol: Given : (1/1.4) + (1/4.7) + (1/7.10) + … + [1/{(3n−2)(3n+1)}] = n/3n+1.
Now, we shall we prove that P(m+1) is true.

Que-14: (1/2) + (1/4) + (1/8) + … + (1/2^n) = 1 − (1/2^n).

Sol: Given : (1/2) + (1/4) + (1/8) + … + (1/2^n) = 1 − (1/2^n).
For n = 1 ; 1/2 = 1 – (1/2¹)  P(1) is true
Let us assume that P(m) is true, where m ∈ N

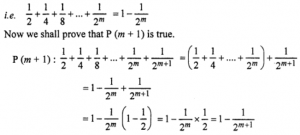
P(m+1) is true.
Hence by mathematical induction P(n) is true for all n ∈ N

Que-15: 1 + 5 + 12 + 22 + 35 + … + (n/2) (3n – 1) = {n²(n+1)}/2.

Sol: Let P (n) be the statement: 1 + 5 + 12 + 22 + … + (n/2) (3n – 1) = {n²(n+1)}/2
For n = 1; 1 = {1²(1+1)}/2 ∴ P(1) is true.
Let us assume that P (m) is true, where m ∈ N
i.e. 1 + 5 + 12 + 22 + … + (m/2) (3m – 1) = {m²(m+1)}/2 … (1)
Now we shall prove that P (m + 1) is true.

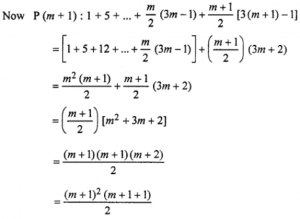
Hence by mathematical induction, P (n) is true for all n ∈ N.

Que-16: Prove by the method of mathematical induction that
(1/4.7) + (1/7.10) + (1/10.13) + … + [1/{(3n+1)(3n+4)}] = n/{4(3n+4)}, for n ∈ N.

Sol: Let P(n) be the statement : (1/4.7) + (1/7.10) + (1/10.13) + … + [1/{(3n+1)(3n+4)}] = n/{4(3n+4)}
For n = 1 ; 1/4.7 = 1/{4(3.1+4)} = 1/28  P(1) is true.
Let us assume that P(m) is true, where m ∈ N
i.e.,  (1/4.7) + (1/7.10) + … + [1/{(3n+1)(3n+4)}] = n/{4(3n+4)}
Now we shall prove that P(m+1) is true

Que-17: Let S (k) = 1 + 3 + 5 +… + (2k – 1) = 3 + k², then which of the following is true ?
(a) S (k) = S (k + 1)
(b) S(k) ≠ S(k + 1)
(c) S (1) is correct
(d) Principle of mathematical induction can be used to prove the formula.

Sol: Given S (k) = 1 + 3 + 5 …. + (2k – 1) = 3 + k²
Here S (1); 1 ≠ 4 – 3 + 1²
∴ S (1) is not true.
Thus option (d) is not correct as basic step of mathematical induction is not true.
∴ S(k + 1)= 1 +3 + 5 + … + [2(k + 1) – 1]
= 1 + 3 + 5 + … + (2k + 1)
= (1 + 3 + 5 + … + 2k – 1) + 2k + 1
= 3 + k² + 2k + 1
= 3 + (k + 1)²
∴ S(k) ≠ S(k+ 1)

–: End of Mathematical Induction Class 11 OP Malhotra Exe-8A ISC Math Ch-8 Solution :–

Return to :- OP Malhotra ISC Class-11 S Chand Publication Maths Solutions

Thanks

Please share with your friends