ML Aggarwal Pythagoras Theorem MCQs Class 9 ICSE Maths Solutions

ML Aggarwal Pythagoras Theorem MCQs Class 9 ICSE Maths Solutions Ch-12. Step by Step Solutions of MCQs on Pythagoras Theorem of ML Aggarwal for ICSE Class 9th Mathematics. Visit official website CISCE for detail information about ICSE Board Class-9.

ML Aggarwal Pythagoras Theorem MCQs Class 9 ICSE Maths Solutions Ch-12

Board	ICSE
Subject	Maths
Class	9th
Chapter-12	Pythagoras Theorem
Topics	Solution of MCQs
Academic Session	2024-2025

MCQs on Pythagoras Theorem

ML Aggarwal Pythagoras Theorem Class 9 ICSE Maths Solutions Ch-12

Question 1. In a ∆ABC, if AB = 6√3 cm, BC = 6 cm and AC = 12 cm, then ∠B is

(a) 120
(b) 90°
(c) 60°
(d) 45°

Answer : (b) 90° is correct 

Hint:  Here largest side is 12 cm.

If square of the hypotenuse is equal to square of other two sides, then it is a right angled triangle.

∴ c² = a² + b²

AC² = AB² + BC²

(12)² = (63)² + (6)²

44 = 36 × 3 + 36

144 = 108 + 36

144 = 144

∴ ∆ABC is a right angled triangle and angle opposite to hypotenuse, ∠B = 90°.

Question 2. If the sides of a rectangular plot are 15 m and 8 m, then the length of its diagonal is

(a) 17 m
(b) 23 m
(c) 21 m
(d) 17 cm

Answer :  (d) 17 cm is correct

Hint:  so the the length of this diagonal is given by square root of sum of squares of sides.

length of diagonal =[15² +8)² ])^1/2

=(225 + 64)² 1/2

=(289)² 1/2=17

hence the length of diagonal is 17 m.

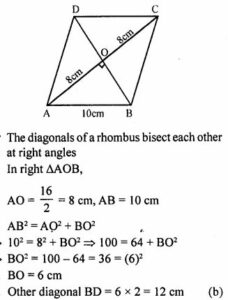
Question 3. The lengths of the diagonals of a rhombus are 16 cm and 12 cm. The length of the side of the rhombus is

(a) 9 cm
(b) 10 cm
(c) 8 cm
(d) 20 cm

Answer :  (b) 10 cm is correct 

Hint:  A rhombus ABCD is there, the diagonals bisect each other at a point O. Let the side of rhombus be AB.

1st diagonal = AC =16 cm

2nd diagonal = BD = 12 cm

AO = AC/2 = 16/2= 8 cm

OB = BD/2 = 12/2 = 6 cm

By Pythagoras theorem,

AO²+ OB² = AB²

8^2+6^2 = AB²

64+36 = AB²

100 = AB²

√100 = AB

10 cm = AB

So the length of the side is 10 cm.

Question 4. If a side of a rhombus is 10 cm and one of the diagonals is 16 cm, then the length of the other diagonals is

(a) 6 cm
(b) 12 cm
(c) 20 cm
(d) 12 cm

Answer :  (b) 12 cm is correct 

Hint:  One diagonal of rhombus = 16 cm

Side = 10 cm

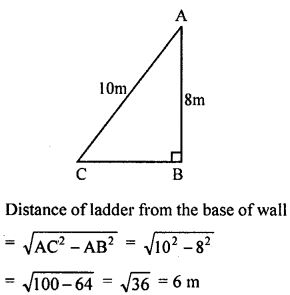
Question 5. If a ladder 10 m long reaches a window 8 m above the ground, then the distance of the foot of the ladder from the base of the wall is

(a) 18 m
(b) 8 m
(c) 6 m
(d) 4 m

Answer :  (c) 6 m is correct

Hint:  Length of ladder = 10 m

Height of window = 8 m

Question 6. A girl walks 200 m towards East and then she walks I5O m towards North. The distance of the girl from the starting point is

(a) 350 m
(b) 250 m
(c) 300 m
(d) 225 m

Answer :  (b) 250 m is correct 

Hint:  A girl walks 200 m towards East and then walks I5O m towards North

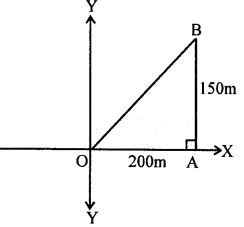
Distance of girls from the stating point

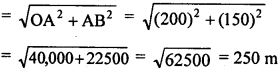
Question 7. A ladder reaches a window 12 m above the ground on one side of the street. Keeping its foot at the same point, the ladder is turned to the other side of the street to reach a window 9 m high. If the length of the ladder is 15 m, then the width of the street is

(a) 30 m
(b) 24 m
(c) 21 m
(d) 18 m

Answer :  (c) 21 m is correct

Hint:  Height of window = 12 m

Length of ladder = 15m

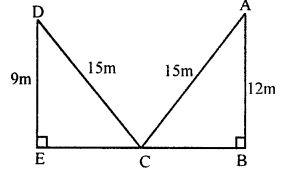
In right triangle ABC

EC = 12 m

width of street EB = EC + CB

= 9 + 12 = 21m

—  : End of ML Aggarwal Pythagoras Theorem MCQs Class 9 ICSE Maths Solutions :–

Return to :-  ML Aggarawal Maths Solutions for ICSE  Class-9

Thanks

Please Share with Your Friends