Mid Point and Intercept Theorems Class 9 OP Malhotra Exe-9A ICSE Maths Solutions Ch-9. We Provide Step by Step Solutions / Answer of Questions as latest edition. Visit official Website CISCE for detail information about ICSE Board Class-9 Mathematics.
Mid Point and Intercept Theorems Class 9 OP Malhotra Exe-9A ICSE Maths Solutions Ch-9
| Board | ICSE |
| Publications | S Chand |
| Subject | Maths |
| Class | 9th |
| Chapter-9 | Mid Point and Intercept Theorems |
| Writer | OP Malhotra |
| Exe-9A | Solved Problems on Mid Point and Intercept Theorems |
| Edition | 2025-2026 |
Solved Problems on Mid Point and Intercept Theorems
Class 9 OP Malhotra Exe-9A ICSE Maths Solutions Ch-9
Que-1: Fill in the blanks :
(i) The line joining the mid-points of two sides of a triangle is …………. to the third side.
(ii) The line drawn through the mid-point of one side of a triangle parallel to another side bisects the …………. side.
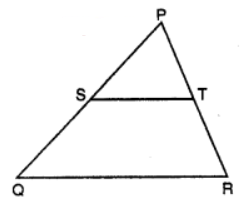
(iii) In figure, S and T are the mid-points of PQ and PR respectively. If ST = 3 cm, then QR = ………….
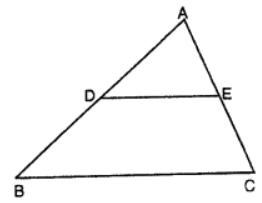
(iv) In figure, D and E are the mid-points of AB and AC. If DE = 7.5 cm, then BC = ………….
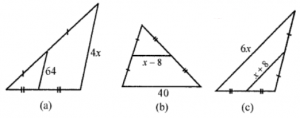
(v) Find the value of x in each triangle.
Sol: (i) The line joining the mid-points of two sides of a triangle is parallel to the third side.
(ii) The line drawn through the mid-point of one side of a triangle parallel to another side bisects the third side.
(iii) In figure, S and T are the mid-points of PQ and PR respectively. If ST = 3 cm, then QR = 6 cm.
(iv) In figure, D and E are the mid-points of AB and AC. If DE = 7.5 cm, then BC = 15 cm.
(v) (a) In the given figure,
In ∆ABC, AD = DB and CE = EB
D and E are the mid points of AB and BC respectively
∴ DE || AC
∴ DE = (1/2) AC and DE || AC
64 = (1/2) x 4x
⇒ 2x = 64
⇒ x = 64/2 = 32
(b) In ∆ABC,
AD = DB and AE = EC
∴ DE || BC and
DE = (1/2) BC
⇒ x – 8 = (1/2) x 40
⇒ x – 8 = 20
⇒ x = 20 + 8 = 28
∴ x = 28
(c) In ∆ABC,
AD = DC and BE = EC
∴ DE || AB and DE = (1/2) AB
x + 8 = (1/2) x 6x
⇒ x + 8 = 3x
⇒ 3x – x = 8
⇒ 2x = 8 ⇒ x = 8/2 = 4
∴ x = 4
Que-2: In ∆ABC, AB = 6 cm, and AC = 3 cm. If M is the mid-point of AB, and a straight line through M parallel to AC cuts BC in N, what is the length of MN?
Sol: In ∆ABC, AB = 6 cm, AC = 3 cm
M is mid point of AB

A line through M is drawn parallel to AC which cuts BC in N
∵ M is mid point of AB and MN || AC
∴ N is mid point of BC
∴ MN = (1/2) AC
= (1/2) x 3 cm = 1.5 cm
Que-3: In the figure, in the ∆ABC, D is the mid-point of AB, E is the mid-point of AC. Calculate:
(i) DE, if BC = 6 cm
(ii) ∠ADE, if ∠DBC = 140°
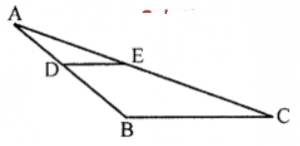
Sol: In the figure,
∆ABC, D is mid-point of AB and E is mid-point of AC
∴ DE || BC and DE = (1/2) BC
(i) ∵ BC = 6 cm
∴ DE = (1/2) x 6 = 3 cm
(ii) ∵ ∠DBC = 140°
∵ DE || BC
∴ ∠ADE = ∠DBC or ∠ABC
(corresponding angles)
∴ ADE = 140°
Que-4: In figure, D, E, F are the mid-points of BC, CA and AB respectively. Prove that AD bisects EF.
Sol: Given : D, E and F are the mid-points of the sides BC, CA and AB respectively AD and EF are joined

AD bisects EF
Construction : Join ED and FD
Proof: In ∆ABC
E and F are the mid-points of CA and AB 1
∴ EF || BC and EF = (1/2) BC
Similarly we can prove that
ED || AB and equal to (1/2) AB
and FD || AC and equal to (1/2) AC
∴ ∆EDF is a parallelogram
∵ The diagonals bisect each other
∴ AD bisects EF
Que-5: In figure, ABC is an isosceles triangle in which AB = AC. D, E and F are respectively the mid-points of sides BC, AB and CA. Show that the line segments AD, EF bisect each other at right angles.

Sol: Given : ∆BC is an isosceles triangle in which AB = AC
D, E and F are the mid-points of BC, AB and AC respectively
AD and EF are joined
AD and EF are perpendicular to each other
Proof: ∵ E and F are mid-points of AB and AC
∴ AE = EB and AF = FC
But AB = AC (given)
∴ AE = AF
and EF || BC and EF = 12 BC
Now in ∆ABD and ∆ACD
AB = AC (given)
BD = DC (D is mid-point)
AD = AD (common)
∴ ∆ABD = ∆ACD (SSS axiom)
∴ ∠BAD = ∠CAD (c.p.c.t)
Now in ∆AEG and ∆AFG
AG = AG (common)
AE = AF ((1/2) of equal sides)
∠BAD or ∠EAG = ∠CAD or ∠AFG (proved)
∴ ∆AEG ≅ ∆AFG (SAS axiom)
∴ ∠AGE = ∠AGF (c.p.c.t.)
But ∠AGE + ∠AFG = 180° (Linear pair)
∴ ∠AGE = ∠AGF = 90°
∴ AD and EF are perpendicular to each other
Hence proved.
Que-6: Prove that the four triangles formed by joining the pairs of mid-points of the three sides of a triangle are congurent to each other.
Sol: Given : In ∆ABC, D, E and F are the mid-points of the sides BC, CA and AB respectively
DE, EF and FD are joined
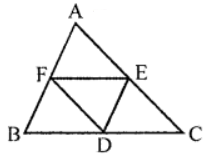
∆AEF ≅ ∆BDF
∆DEF ≅ ∆CDE
Proof: ∵ D and E are the mid-points of side BC and CA respectively
∴ DE || AB and DE = (1/2) AB
∴ DE = BF = FA … (i)
Similarly, D and F are the mid-points of BC and AB respectively
∴ DF || AC and DF = –(1/2) AC … (ii)
DF = AE = EC
Now in ∆AEF and ∆DEF
AF = DE (proved)
AE = DF (proved)
EF = EF (common)
∴ ∆AEF ≅ ∆DEF … (i) (SSS criteria)
Similarly we can prove that
∆BDF ≅ ∆DEF … (i)
and ∆CDE ≅ ∆DEF … (ii)
From (i), (ii) and (iii)
∆AEF ≅ ∆BDF ≅ ∆CDE ≅ ∆DEF
Hence proved.
Que-7: D, E and F are respectively the mid-points of the sides BC, CA and AB of an equilateral triangle ABC. Prove that ∆DEF is also an equilateral triangle.
Sol: Given : ∆ABC is an equilateral triangle. D, E and F are the mid-points of sides BC, CA and AB respectively
DE, EF and FD are joined
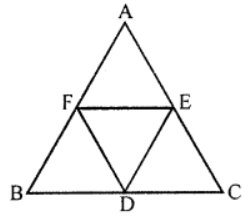
∆DEF is an equilateral triangle
Proof:
∵ E and F are the mid-points of AC and AB respectively
∴ EF || BC and EF = (1/2) BC … (i)
Similarly, D and E are the mid-points of BC and AC respectively
∴ DE || AB and DE = (1/2) AB … (ii)
and D and F are the mid-points of BC and AB respectively
∴ DF || AC and DF = (1/2) AC … (iii)
From (i), (ii) and (iii)
∵ AB = BC = CA (sides of equilateral ∆ABC)
∴(1/2) EF = (1/2) DE = (1/2) DF
⇒ DE = EF = FD
∴ ∆DEF is an equilateral triangle
Hence proved.
Que-8: In figure, AD and BE are the medians of ∆ABC and BE || DF. Prove that CF = (1/4)AC
Sol: Given: In AABC, AD and BE are its median BE || DF

CF = (1/4) AC
Proof:
∵ BE is the median
∴ E is mid-point of AC
∴ AE = EC or EC = (1/2) AC … (i)
In ∆BCE,
D is mid-point of BC and DF || BE
∴ F is mid-point of EC
∴ FC = (1/2) EC … (iv)
From (i) and (ii),
CF = (1/2) EC = (1/2) ((1/2) AC) = (1/4)AC
Hence CF = (1/4) AC
Hence proved.
Que-9: In the given figure, ABC is an isosceles A with AB = AC and CP || BA and AP is the bisector of ext. ∠CAD of ∆ABC. Prove that
(i) ∠PAC = ∠BCA
(ii) ∆BCP is a parallelogram.
Sol: Given : ∆ABC is an isosceles triangle in which AB = AC
CP || BA is drawn and AP is the bisector of ∠CAD
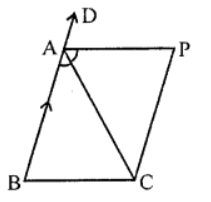
(i) ∵ AB=AC (given)
∴ ∠C = ∠B (Angles opposite to equal sides)
But Ext. ∠CAD = ∠B + ∠C= 2∠C … (i)
(Sum of its interior opposite angles)
and ∠PAC = ∠PAD = (1/2) ∠CAP … (ii)
From (i) and (ii),
∠C = ∠CAP or ∠PAC = ∠BCA
(ii) ∵∠PAC = ∠BCA (proved)
But these are alternate angles
∴ AP || BC
But CP || BA
∴ ABCP is a parallelogram
Hence proved.
Que-10: ABCD is a kite having AB = AD and BC = CD. Prove that the figure formed by joining the midpoints of the sides, in order, is a rectangle.
Sol: Given: In the figure, ABCD is a kite in which AB = AD and BC = DC
P, Q, R and S are the mid-points of the sides AB, AD, DC and BC respectively
PQ, QR, RS and PS are joined
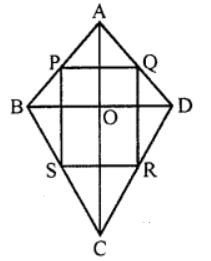
Construction : Join BD and AC
Proof: In ∆ABD,
∵ P and Q are mid-points of AB and AD respectively
∴ PQ || BD and PQ = (1/2) BD … (i)
Similarly in ABCD,
S and R are the mid-points of BC and DC
∴ SR || BD and SR = (1/2) BD … (ii)
From (i) and (ii)
∴ PQ = SR and PQ || SR
Similarly PS = QR and PS || QR
∴ PQRS is a parallelogram
∵ Diagonals AC and BD intersect
Each other at right angles
∴ PQRS is a rectangle
Hence proved.
Que-11: Show that the quadrilateral, formed by joining the mid-points of the consecutive sides of a rectangle, is a rhombus.
Sol: Given : ∆BCD is a rectangle. P, Q, R, and S are the mid-points of the sides AB, BC, CD and DA respectively PQ, QR, RS and SP are joined
To prove : PQRS is a rhombus
Construction : Join PR and SQ, AC and BD are also joined
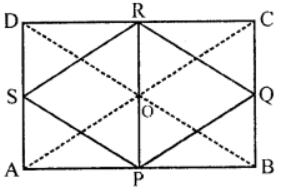
In ∆ABC,
∵ P and Q are mid-points of AB and BC respectively
∴ PQ || AC and PQ = (1/2) AC … (i)
Similarly in ∆ADC,
∴ S and R are the mid-points of AD and CD respectively
∴ SR || AC and SR = (1/2) AC … (ii)
From (i) and (ii)
PQRS is a parallelogram
Similarly PS || BD and SP = (1/2) BD 1
and QR || BD and QR = (1/2) BD
But in rectangle ABCD diagonals AC and BD are equal
∴ PQRS is a rhombus
Hence proved.
Que-12: Quad. ABCD is a rhombus and P, Q, R, S are the mid-points of AB, BC, CD, DA respectively. Prove that quad. PQRS is a rectangle.
Sol: Given : ABCD is a quad, which is a rhombus. P, Q, R and S are the mid-points of the sides AB, BC, CD and DA respectively PQ, QR, RS and SP are joined
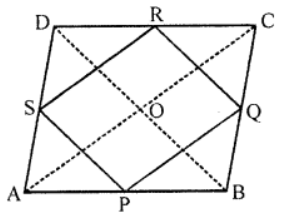
PQRS is a rectangle
Construction : Join AC and BD
Proof: In ∆ABC
∵ P and Q are the mid-points of AB and CD respectively
∴ PQ || AC and PQ = (1/2) AC … (i)
Similarly in ∆ADC,
R and S are the mid-points of CD and DA respectively
∴ RS || AC and RS = (1/2) AC … (ii)
∴ PQRS is a parallelogram
∵ Diagonals of rhombus bisect each other at right angles PQRS is a rectangle
Hence proved.
Que-13: In the quadrilateral ABCD the mid-points of AB, BC, CD, DA are L, M, P, Q.
(i) Using the mid-point theorem make a statement concerning the lengths and directions of LM and AC.
(ii) Prove that LMPQ is a parallelogram.
(iii) If it is also given that the diagonals AC and BD are equal. What further statement can be made about the parallelogram LMPQ ?
Sol: Given : In quadrilateral ABCD, L, M, Pand Q are the mid-points of the sides AB, BC, CD and DA respectively. LM and AC are joined.
(i) ∵ L and M are the mid-points of AB and BC respectively
∴ LM || AC and LM = (1/2) AC … (i)
(ii) Similarly P and Q are the mid-points of CD and DA respectively
∴ PQ || AC and PQ = (1/2) AC … (ii)
From (i) and (ii),
LMPQ is a parallelogram
(iii) If diagonals AC and BD are equal
Then ABCD can be a parallelogram or a rectangle
Then LM = MP = PQ = QL Then LMPQ will be a rhombus
(∵ If the sides of a parallelogram are equal then it is a rhombus)
Que-14: ABCD is a parallelogram E is the mid-point of AB and F is the mid-point of CD. GH is any line that intersects AD, EF and BC in G, P and H respectively. Prove that GP = PH.
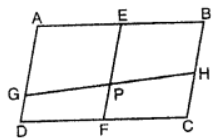
Sol: Given : In the figure ABCD is a parallelogram. E and F are the mid-points of AB and CD respectively GH is any line which intersects AD in G, EF in P and BC in H
E and F are the mid-points of AB and DC respectively
∴ EF || AD || BC (∵ ABCD is a parallelogram)
∴ AE = EB ⇒ AE/EB = 1
∴ GP/PH = 1 ⇒ GP = PH (intercept theorem)
Hence proved.
Que-15: Prove that in a parallelogram, the lines joining a pair of opposite vertices to the mid-points of a pair of opposite sides trisect a diagonal.
Sol: Given : In ||gm ABCD, E and F are the mid-points of side AD and BC respectively
EB and DF are joined which intersect diagonal AC at M and N
To prove : M and N trisect AC
i.e. AM = MN = NC
Proof: ∵ E and F are the mid-points of AD and BC respectively
∴ BE || DF
Now in ∆ADN,
∵ EM || DN and AE = ED
AM = MN … (i)
Similarly in ∆BCM,
∵ CF = FB
∴ CN = NM … (ii)
From (i) and (ii),
AM = MN = NC
Hence M and N trisect AC
Hence proved.
Que-16: In figure, E is the mid-point of side AD of a trapezium ABCD, with AB || DC. A line through E parallel to AB, meets BC in F. Show that F is the mid-point of BC.
Sol: Given : In trapezium ABCD, AB || DC
E is mid-point of AD
A line through E is drawn parallel to AB which meets BC in F
To prove : F is the mid-point of BC
Proof: In ∆ADB,
∵ E is mid-point of AD and EO orEF is parallel toAB
∴ O is mid-point of BD
Similarly in ∆BCD,
O is mid-point of BD and EOF || CD (||AB)
∴ F is mid-point BC
Hence proved.
— : End of Triangles Class 9 OP Malhotra Exe-8C ICSE Maths Ch-8 Solutions:–
Return to :– OP Malhotra S Chand Solutions for ICSE Class-9 Maths
Thanks
Please Share with Your Friends


