Miscellaneous Numerical on Capacitors and Dielectrics Class-12 Nootan ISC Physics Ch-4 Capacitors and Dielectrics. Step by step solutions of Kumar and Mittal Physics of Nageen Prakashan as council latest prescribe guideline for upcoming exam. Visit official Website CISCE for detail information about ISC Board Class-12 Physics.

Miscellaneous Numerical on Capacitors and Dielectrics Class-12 Nootan ISC Physics Ch-4
| Board | ISC |
| Class | 12 |
| Subject | Physics |
| Book | Nootan |
| Chapter-4 | Capacitors and dielectrics |
| Topics | Miscellaneous Numerical |
| Academic Session | 2025-2026 |
Miscellaneous Numerical on Capacitors and Dielectrics
Class-12 Nootan ISC Physics Ch-4 Capacitors and Dielectrics.
Que-43. Calculate the equivalent capacitance between the points A and B in the given circuit. If 100 V PD is established between A and B then what will be the charge on the capacitor closest to?
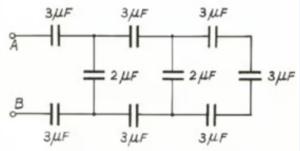
Ans-43 3μF capacitor in series
their net capacitor = 3/3 = 1μF
∴ again this series combination is in parallel with 2μF
∴ net capacitance = 2+1 = 3μF
Solving similarly we have net capacitance of combination = 1μF
Charge in combination
Q = CV
= 1 x 100 = 100 μC.
Que-44. Find the equivalent capacitance between the points A and B in the given circuit.
Ans-44 This combination is an example of Wheat Stone Bridge (to be decreased in later chapters) in which the middle capacitor becomes in effective therefore above and lower 2μF capacitors combination are in parallel with in each series
i.e., (2/2) + (2/2) = 2μF.
Que-45. Four capacitors of equal capacitances are joined in series with a battery of 10 V. The middle point B is connected to the earth. What will be the potentials of the points A and C?
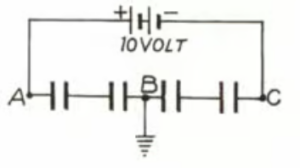
Ans-45 Pointed B which is earthed will be at zero potential
Since 4 capacitors are equal therefore,
VA – VB = VB – VC
= VA + VC = 2VB = 0 …….(i)
and VA – VC = 10 ……….(ii)
On adding both equations we get,
2VC = -10
VC = -5
VA = 5.
Que-46. A parallel-plate capacitor with no dielectric has a capacitance of 0.5 µF. The space between the plates is then filled with equal amounts of two dielectrics of dielectric constants 2 and 3 in the two arrangements as shown one by one. Find the ratio of capacitances C₁ and C.
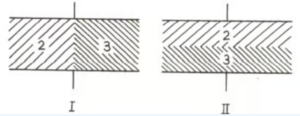
Ans-46 The first case can be considered as the capacitors in parallel
Equivalent capacitance is equal to
CA = k1C1 + k2C2
= 2(Aε0/2d) + 3(Aε0/2d)
= (5/2) × 0.5μF
The second case can be considered as the capacitors in series
Equivalent capacitance is equal to
1/C = [1/(k1C1)] + [1/(k2C2)]
= [d/(2×2Aε0)] + [d/(3×2Aε0)]
CB = (12/5) × 0.5μF
CA/CB = 25/24.
Que-47. As shown in figure, a dielectric substance of dielectric constant K is inserted in half of the portion between the plates of a parallel- plate capacitor. If its initial capacitance is C, then what will be the new capacitance?
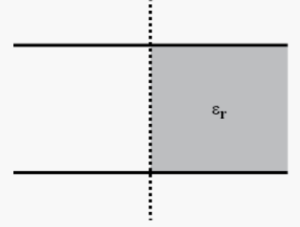
Ans-47 It is composed of two capacitor in parallel with same depth and area
(C/2) + (1/2)kC
(1/2)C (1+k).
Que-48. Figure shows charge (q) versus voltage (V) graph for series and combination parallel of two given capacitors. Find the value of the capacitance of the given capacitors.
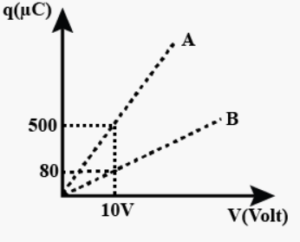
Ans-48 Given in the figure,
Charge, q1 = 500 μC
Charge, q2 = 80 μC
Voltage, V = 10 V
Equivalent capacitance in series combination (C) is given by
1/C’ = 1/C1 + 1/C2
⇒ C′ = {C1C2/(C1+C2)}
For parallel combination, equivalent capacitance is given by,
C” = C1 + C2
For parallel combination,
q1/𝑉 = (C1+C2)
500/10 = (𝐶1+𝐶2)
(C1 + C2 ) = 50 μF —-(1)
For series combination,
q2/𝑉 = {C1C2/(C1+C2)}
80/10 = {(C1C2)/50}
C1 C2 = 8 × 50
C1 C2 = 400 —-(2)
Let 𝐶1 = 400/𝐶2
Substitute this in equation (1), we get
400/𝐶2 + 𝐶2 = 50
400 + 𝐶²2 = 50𝐶2
𝐶²2−50𝐶2+400 = 0
𝐶²2−10𝐶2−40𝐶2+400 = 0
C2(C2 – 10) – 40(C2 – 10) = 0
(C2 – 10)(C2 – 40) = 0
C2 = 10 μF or C2 = 40 μF
Que-49. The two plates of a parallel plate capacitor are 4 mm apart. A slab of dielectric constant 3 and thickness 3 mm is introduced between the plates with its faces parallel to them. The distance between the plates is so adjusted that the capacitance of the capacitor becomes 2/3 rd of its original value. What is the new distance between the plates?
Ans-49 C = Aε0/{d-t+(t/k)} = {Aε0/4} x 2/3
Aε0/4 = C
6 = d-t+(t/k)
6 = d-3+(3/3)
6 = d-3+1
6 = d-2
d = 6+2 = 8mm.
Que-50. X and Y are two parallel plate capacitors having the same areas of plates and same separation between the plates. X has air between the plates and Y contains a dielectric medium Er = 4.
(i) Calculate the capacitance of each capacitor if equivalent capacitance of the combination is 4 μF.
(ii) Calculate the potential difference between the plates of X and Y.
(iii) What is the ratio of electrostatic energy stored in X and Y?
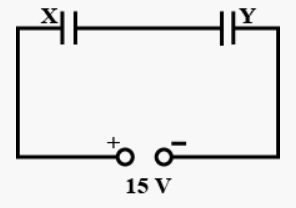
Ans-50 (i) Let the area of the plates be A and distance between the plates be d
∴ Capacitance of capacitor X C1 = Aϵo/d
Also capacitance of capacitor Y C2 = ErAϵo/d = 4Aϵo/d = 4C1
Equivalent capacitance in series combination, C eq = {C1×C2}/(C1+C2)
∴ 4μF = {C1×4C1}/(C1+4C1)
OR 4μF = 4C1/5
⟹ C1 = 5μF
∴ C2 = 4×5μF = 20μF
(ii) q1 = q2 = CsV = 4×12 = 48μC
V1 = q1/C1 = 48/5 = 9.6V
V2 = q2/C2 = 48/20 = 2.4V
(iii) Electrostatic energy stored in a capacitor E = Q²/2C
∴ E1/E2 = [Q²/2C1]/[Q²2C2] = C2/C1 = 20μF/5μF = 4.
Que-51. A system of capacitors connected as shown in the figure has total energy of 160 mJ stored in it. Obtain the value of the equivalent capacitance of this system and the value of Z.
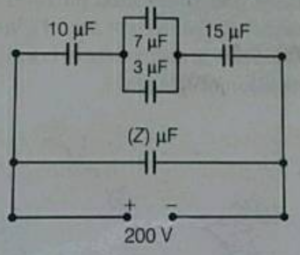
Ans-51 In the arrangement of capacitors shown , capacitors of capacitances C2 and C3 are joined in parallel and their equivalent capacitance C23 = 7+3 = 10μF
Now C1, C23 and C4 are joined in series , hence their equivalent capacitance C. is given by
1/C. = 1/C1+1/C23+1/C4 = 1/10+1/10+1/15 = 8/30
⇒ C. = 30/8μF = 3.75μF
As C5 is in parallel to C. , hence equivalent capacitance Ceq of the arrangement is Ceq =
C.+z = (3.75+z)μF
∴ Energy of the system U = 1/2Ceq, V² , where U = 160 mJ = 0.16 J and V = 200 V
∴0.16 = 1/2 × Ceq (200)²
⇒ Ceq = (0.16×2)/(200)² = 8×10^−6 F = 8μF
As Ceq = (3.75+z) = μF = 8μF , hence we have z = 4.25μF
— : End of Miscellaneous Numerical on Capacitors and Dielectrics Class-12 Nootan ISC Physics Ch-4. :–
Return to : – Nootan Solutions for ISC Class-12 Physics
Thanks
Please share with your friends