ML Aggarwal Algebra Exe-9.5 Class 6 ICSE Maths Solutions. We Provide Step by Step Answer of Exe-9.5 Questions for Algebra as council prescribe guideline for upcoming board exam. Visit official Website CISCE for detail information about ICSE Board Class-6.
ML Aggarwal Algebra Exe-9.5 Class 6 ICSE Maths Solutions
| Board | ICSE |
| Publications | Avichal Publishig Company (APC) |
| Subject | Maths |
| Class | 6th |
| Chapter-9 | Algebra |
| Writer | ML Aggarwal |
| Book Name | Understanding |
| Topics | Solution of Exe-9.5 Questions |
| Edition | 2023-2024 |
Algebra Exe-9.5
ML Aggarwal Class 6 ICSE Maths Solutions
Page-198
Question 1. State which of the following are equations with a variable. In case of an equation with a variable, identify the variable.
(i) 17 + x = 5
(ii) 2b – 3 = 7
(iii) (y – 7) > 5
(iv) 9/3 = 3
(v) 7 × 3 – 19 = 2
(vi) 5 × 4 – 8 = 31
(vii) 2p < 15
(viii) 7 = 11 × 5 – 12 × 4
(ix) 3/2 q = 5
Answer:
(i) 17 + x= 5 Is an equation → L.H.S. = R.H.S. → Related variable x.
(ii) 2b – 3 = 7 Is an equation → L.H.S. = R.H.S. → Related variable b.
(iii) (y- 7) >5
Is not an equation → L.H.S. ≠ R.H.S.
It has no sign of equality (=).
(iv) 9/3 = 3
Is an equation = L.H.S. = R.H.S.
It has no variable.
(v) 7 × 3 – 19 = 2
Is an numerical equation = L.H.S. = R.H.S. It has no variable.
(vi) 5 × 4 – 8 = 31
Is an equation = L.H.S. = R.H.S. → Related variable t.
(vii) 2p < 15
Is not an equation = L.H.S. ≠ R.H.S.
It has no sign of equality.
(viii) 7 = 11 × 5 – 12 × 4
Is an numerical equation = L.H.S. = R.H.S. It has no variable.
(ix) 3/2 q = 5
Is an equation → L.H.S. = R.H.S. → Related variable q.
Question 2. Solve each of the following equations :
(i) x + 6 = 8
(ii) 2 – x = 5
(iii) 4x = -6
(iv) x/2 = 5
(v) 2y – 3 = 2
(vi) 4 – 5y = 2
Answer:
(i) x + 6 = 8
= x = 8 – 6 ⇒ x = 2
(ii) 2 – x = 5
= -x = 5 – 2 ⇒ -x = 3 ⇒ x = – 3
(iii) 4x = -6
(iv) x/2 = 5
= x = 5 × 2 ⇒ x = 10
(v) 2y – 3 = 2
= 2y = 2 + 3 ⇒ 2y = 5 ⇒ y = 5/2
(vi) 4 – 5y = 2
= 4 – 2 = 5y ⇒ 5y = 2
⇒ y = 2/5
Question 3. Solve the following linear equations:
(i) 5(x + 1) = 25
(ii) 2(3x – 1) = 10
(iii) (3x – 1)/4 = 11
Answer:
(i) 5(x + 1) = 25
⇒ 5(x + 1)/5 = 25/5 (dividing both sides by 5)
⇒ x + 1 = 5
⇒ x + 1 – 1 = 5 – 1 (Subtracting 1 from both sides)
⇒ x = 4
(ii) 2(3x – 1) = 10
⇒ 2(3x – 1)/2 = 10/2 (dividing both sides by 2)
⇒ 3x – 1 = 5
⇒ 3x – 1 + 1 = 5 + 1 (adding 1 to both sides)
⇒ 3x = 6
⇒ 3x/3 = 6/3 (dividing both sides by 3)
⇒ x = 2
(iii) Given (3x – 1)/4 = 11
⇒ 4 × (3x – 1)/4 = 4 × 11 (multiplying both sides by 4)
⇒ 3x – 1 = 44
⇒ 3x – 1 + 1 = 44 + 1 (adding 1 to both sides)
⇒ 3x = 45
⇒ 3x/3 = 45/3 (dividing both sides by 3)
⇒ x = 15
Question 4. Solve the following linear equations:
(i) 5x – 6 = 12 – x
(ii) n/3 + 1 = 4 – n
(iii) 5p + 7 = 19 – 2p
(iv) 2x + 5/2 = 2/3 -x
(v) x/2 -5 = x/3 -4
(vi) 18 – (3y/4) = 11 + y
Answer:
(i) 5x – 6 = 12 – x
⇒ 5x + x = 12 + 6
6x = 18 ⇒ x = 18/6 = 3
Verification
5x − 6 = 12 − x
⇒ 5(3) − 6 = 12 − 3
⇒ 15 – 6 = 9
⇒ 9 = 9
(ii) n/3 + 1 = 4 – n

(iii) 5p + 7 = 19 – 2p
⇒ 5p + 2p = 19 – 7
⇒ 7p = 12
⇒ p 12/7
Verification
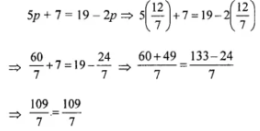
(iv) 2x + 5/2 = 2/3 -x

(v) x/2 – 5 = x/3 -4
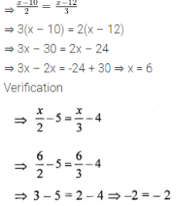
(vi) 18 – (3y/4) = 11 + y

Question 5. Solve the following equations and verify your answers:
(i) 3(x + 7) = 18
(ii) 2(x- 1) = x + 2
(iii) 3x – 1/2 = 2( x – 1/2) + 5
(iv) 4(2x – 1) -2(x – 5) = 5(x + 1) + 3
Answer:
(i) 3(x + 7) = 18
⇒ 3x + 21 = 18
⇒ 3x = 18 − 21
⇒ 3x = −3
⇒ x = -3/3
x = −1
Verification
⇒ 3(x + 7) = 18
⇒ 3(−1 + 7) = 18
⇒ 3(6) = 18
⇒ 18 = 18
(ii) 2(x − 1) = x + 2
⇒ 2x − 2 = x + 2
⇒ 2x − x = 2 + 2
⇒ x = 4
Verification
⇒ 2(x − 1) = x + 2
⇒ 2(4 − 1) = 4 + 2
⇒ 2(3) = 6
⇒ 6 = 6
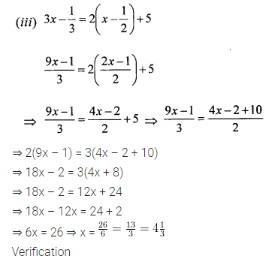
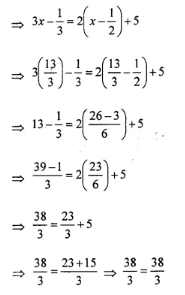
(iv) 4(2x – 1) -2(x – 5) = 5(x + 1) + 3
⇒ 8x − 4 − 2x + 10 = 5x + 5 + 3
⇒ 8x − 2x− 4 + 10 = 5x + 5 + 3
⇒ 6x + 6 = 5x + 8
⇒ 6x – 5x = 8 – 6
⇒ x = 2
Verification :
4(2x − 1) − 2(x − 5) = 5(x + 1) + 3
⇒ 4 (2 × 2-1) – 2(2-5)=5(2+1)+3
⇒ 4 ( 4 – 1) – 2 (-3) = 5 ( 3) + 3
⇒ 4 ( 3) – 2 (-3) = 15 + 3
⇒ 12 + 6 = 18
⇒ 18 = 18
— : End of ML Aggarwal Algebra Exe-9.5 Class 6 ICSE Maths Solutions :–
Return to – ML Aggarwal Maths Solutions for ICSE Class -6
Thanks


