ML Aggarwal Algebraic Expression and Identities Exe-10.3 Class 8 ICSE Ch-10 Maths Solutions

ML Aggarwal Algebraic Expression and Identities Exe-10.3 Class 8 ICSE Ch-10 Maths Solutions. We Provide Step by Step Answer of  Exe-10.3 Questions for Algebraic Expression and Identities as council prescribe guideline for upcoming board exam. Visit official Website CISCE for detail information about ICSE Board Class-8.

ML Aggarwal Algebraic Expression and Identities Exe-10.3 Class 8 ICSE Maths Solutions

Board	ICSE
Publications	Avichal Publishig Company (APC)
Subject	Maths
Class	8th
Chapter-10	Algebraic Expression and Identities
Writer	ML Aggarwal
Book Name	Understanding
Topics	Solution of Exe-10.3 Questions
Edition	2023-2024

Algebraic Expression and Identities Exe-10.3

ML Aggarwal Class 8 ICSE Maths Solutions

Page-178

Question 1. Multiply:

(i) (5x – 2) by (3x + 4)
(ii) (ax + b) by (cx + d)
(iii) (4p – 7) by (2 – 3p)
(iv) (2x² + 3) by (3x – 5)
(v) (1.5a – 2.5b) by (1.5a + 2.56)
(vi) {(3/7)p²+4q²} by 7{p² – (3/4)q²}

Answer:

(i) (5x – 2) by (3x + 4)

= (5x – 2) × (3x + 4)

= 5x (3x + 4) – 2 (3x + 4)

= 15x² + 20x – 6x – 8

= 15x²+ 14x – 8

(ii) (ax + b) by (cx + d)

= (ax + b) × (cx + d)

= ax (cx + d) + b (cx + d)

= acx² + adx + bcx + bd

(iii) (4p – 7) by (2 – 3p)

= (4p – 7) × (2 – 3p)

= 4p(2 – 3p) -7(2 – 3p)

= 8p – 12p² – 14 + 21p

= 29p – 12p² – 14

(iv) (2x² + 3) by (3x – 5)

= (2x² + 3) (3x – 5)

= 2x²(3x – 5) + 3(3x – 5)

= 6x³ – 10x² + 9x – 15

(v) (1.5a – 2.5b) by (1.5a + 2.5b)

= (1.5a – 2.5b) (1.5a + 2.5b)

= 1.5a(1.5 + 2.5b) – 2.5b(1.5a + 2.5b)

= 2.25a² + 3.75ab – 3.75a6 – 6.25b²

= 2.25a² – 6.25b²

(vi) {(3/7)p²+4q²} by 7{p² – (3/4)q²}

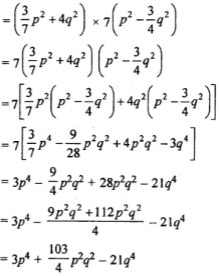
Question 2. Multiply:

(i) (x – 2y + 3) by (x + 2y)
(ii) (3 – 5x + 2 × 2) by (4x – 5)

Answer:

(i) (x – 2y + 3) by (x + 2y)

= (x – 2y + 3) × (x + 2y)

= x (x + 2y) – 2y(x + 2y) + 3 (x + 2y)

= x² + 2xy – 2xy – 4y² + 3x + 6y

= x² – 4y² + 3x + 6y

(ii) (3 – 5x + 2x²) by (4x – 5)

= (4x – 5) (3 – 5x + 2x²)

= 4x(3 – 5x + 2x²) – 5(3 – 5x + 2x²)

= 12x – 20x² + 8x³ – 15 + 25x – 10x²

= 8x³ – 30x² + 37x – 15

Question 3. Multiply:

(i) (3x² – 2x – 1) by (2x² + x – 5)
(ii) (2 – 3y – 5y²) by (2y – 1 + 3y²)

Answer:

(i) (3x² – 2x – 1) by (2x² + x – 5)

= (3x² – 2x – 1) (2x² + x – 5)

= 3x²(2x² + x – 5) – 2x(2x² + x – 5) -1(2x² + x – 5)

= 6x⁴ + 3x³ – 15x² – 4x³ – 2x² + 10x – 2x² – x + 5

= 6x⁴ – x³ – 19x² + 9x + 5

(ii) (2 – 3y – 5y²) by (2y- 1 + 3y²)

= (2 – 3y – 5y²) × (2y- 1 + 3y²)

= 2(2y – 1 + 3y² ) – 3y (2y – 1 + 3y²) -5y²(2y – 1 + 3y²)

= 4y – 2 + 6y² – 6y² + 3y – 9y³ – 10y³ + 5y² – 15y⁴

= -15y⁴ – 19y³ + 5y² + 7y – 2

Question 4. Simplify:

(i) (x² + 3) (x – 3) + 9
(ii) (x + 3) (x – 3) (x + 4) (x – 4)
(iii) (x + 5) (x + 6) (x + 7)
(iv) (p + q – 2r) (2p – q + r) – 4qr
(v) (p + q) (r + s) + (p – q)(r – s) – 2(pr + qs)
(vi) (x + y + z) (x – y + z) + (x + y – z) (-x + y + z) – 4zx

Answer:

(i) (x² + 3) (x – 3) + 9

= x² (x – 3) + 3(x – 3) + 9

= x² – 3x² + 3x – 9 + 9

= x³ – 3x² + 3x

(ii) (x + 3) (x – 3) (x + 4) (x – 4)

= {(x + 3) (x – 3)} × {(x + 4) (x – 4)}

= {x (x – 3) + 3 (x – 3)} {x (x – 4) + 4 (x – 4)}

= (x² – 3x + 3x – 9) {x² – 4x + 4x – 16}

= (x² – 9) (x² – 16)

= x² (x² – 16) – 9 (x² – 16)

= x⁴ – 16x² – 9x² + 144

= x⁴ – 25x² + 144

(iii) (x + 5) (x + 6) (x + 7)

= {(x + 5) × (x + 6)} (x + 7)

= (x² + 6x + 5x + 30) (x + 7)

= (x² + 11x + 30) (x + 7)

= x(x²+ 11x + 30) + 7(x²+ 11x + 30)

= x³ + 11x² + 30x + 7x² + 77x + 210

= x³ + 18x² + 107x + 210

(iv) (p + q – 2r)(2p – q + r) – 4qr

= p(2p – q + r) + q(2p – q + r) – 2r(2p – q + r) – 4qr

= 2p² – pq + pr + 2pq – q² + qr – 4pr + 2qr – 2r² – 4qr

= 2p² – q² – 2r² + pq – 3pr – 2qr

(v) (p + q)(r + s) + (p – q) (r – s) – 2(pr + qs)

= (pr + ps + qr + qs) + (pr – ps – qr + qs) – 2pr – 2qs

= 0

(vi) (x + y + z)(x – y + z) + (x + y – z)(-x + y + z) – 4zx

= x² – xy + xz + xy – y² + yz + xz – yz + z² – x² + xy + xz

– xy + x² + yx + xz – yz – z² – 4zx

= 0

Question 5. If two adjacent sides of a rectangle are 5x² + 25xy + 4y² and 2x² – 2xy + 3y², find its area.

Answer:

The adjacent sides of a rectangle are 5x² + 25xy + 4y² and 2x² – 2xy + 3y²

Area of rectangle = Product of two adjacent sides

= (5x² + 25xy + 4y²) (2x² – 2xy + 3y²)

= 10x⁴– 10x³y+ 15x²y² + 50x³y – 50x²y² + 75xy³ + 8x²y² – 8xy³ + 12y⁴

= 10x⁴ + 40x³y – 27x²y² + 67xy³ + 12y⁴

Hence, the area of the rectangle is 10x⁴ + 40x³y – 27x²y² + 67xy³ + 12y⁴.

— End of Algebraic Expression and Identities Exe-10.3 Class 8 ICSE Maths Solutions :–

Return to : – ML Aggarwal Maths Solutions for ICSE Class -8

Thanks