ML Aggarwal Algebraic Expression and Identities Exe-10.5 Class 8 ICSE Ch-10 Maths Solutions. We Provide Step by Step Answer of Exe-10.5 Questions for Algebraic Expression and Identities as council prescribe guideline for upcoming board exam. Visit official Website CISCE for detail information about ICSE Board Class-8.
ML Aggarwal Algebraic Expression and Identities Exe-10.5 Class 8 ICSE Maths Solutions
| Board | ICSE |
| Publications | Avichal Publishig Company (APC) |
| Subject | Maths |
| Class | 8th |
| Chapter-10 | Algebraic Expression and Identities |
| Writer | ML Aggarwal |
| Book Name | Understanding |
| Topics | Solution of Exe-10.5 Questions |
| Edition | 2023-2024 |
Algebraic Expression and Identities Exe-10.5
ML Aggarwal Class 8 ICSE Maths Solutions
Page-185
Question 1. Using suitable identities, find the following products:
(i) (3x + 5) (3x + 5)
(ii) (9y – 5) (9y-5)
(iii) (4x + 11y) (4x – 11y)
(iv) (3m/2 + 2n/3) (3m/2 – 2n/3)
(v) (2/a + 5/b) (2a + 5/b)
(vi) (p2/2 + 2/q2) (p2/2 – 2/q2)
Answer:
(i) (3x + 5) (3x + 5)
= (3x + 5)2
= (3x)2 + 2 × 3x × 5 + (5)2 [Using, (a + b)2 = a2 + 2ab + b2]
= 9x2 + 30x + 25
(ii) (9y – 5) (9y – 5)
= (9y – 5)2
= (9y)2 – 2 × 9y × 5 + (5)2 [Using, (a – b)2 = a2 – 2ab + b2]
= 81y2 – 90y + 25
(iii) (4x + 11y)(4x – 11y)
= (4x)2 – (11y)2
= 16x2 – 121y2 [Using, (a + b)(a – b) = a2 – b2]
(iv) (3m/2 + 2n/3) (3m/2 – 2n/3)
= (3m/2)2 – (2n/3)2
= 9m2/4 – 4n2/9 [Using, (a + b)(a – b) = a2 – b2]
(v) (2/a + 5/b) (2a + 5/b)
= (2/a + 5/b)2
= (2/a)2 + 2(2/a)(5/b) + (5/b)2 [Using, (a + b)2 = a2 + 2ab + b2]
= 4/a2 + 20a/b + 25/b2
(vi) (p2/2 + 2/q2) (p2/2 – 2/q2)
= (p2/2)2 – (2/q2)2 [Using, (a + b)(a – b) = a2 – b2]
= p4/4 – 4/q4
Question 2. Using the identities, evaluate the following:
(i) 812
(ii) 972
(iii) 1052
(iv) 9972
(v) 6.12
(vi) 496 × 504
(vii) 20.5 × 19.5
(viii) 9.62
Answer:
(i) (81)2 = (80 + 1)2
= (80)2 + 2 × 80 × 1 + (1)2 [Using, (a + b)2 = a2 + 2ab + b2]
= 6400 + 160+ 1
= 6561
(ii) (97)2 = (100 – 3)2
= (100)2 – 2 × 100 × 3 + (3)2 [Using, (a – b)2 = a2 – 2ab + b2]
= 10000 – 600 + 9
= 10009 – 600
= 9409
(iii) (105)2 = (100 + 5)2
= (100)2 + 2 × 100 × 5 + (5)2 [Using, (a + b)2 = a2 + 2ab + b2]
= 10000+ 1000 + 25
= 11025
(iv) (997)2 = (1000 – 3)2
= (1000)2 – 2 × 1000 × 3 + (3)2 [Using, (a – b)2 = a2 – 2ab + b2]
= 1000000 – 6000 + 9
= 1000009 – 6000
= 994009
(v) (6.1)2 = (6 + 0.1)2
= (6)2 + 2 × 6 × 0.1 +(0.1)2 [Using, (a + b)2 = a2 + 2ab + b2]
= 36 + 1.2 + 0.01
= 37.21
(vi) 496 × 504
= (500 – 4) (500 + 4) [Using, (a + b) (a – b) = a2 – b2]
= (500)2 – (4)2
= 250000 – 16
= 249984
(vii) 20.5 × 19.5
= (20 + 0.5) (20 – 0.5) [Using, (a + b) (a – b) = a2 – b2]
= (20)2 – (0.5)2
= 400 – 0.25
= 399.75
(viii) (9.6)2 = (10 – 0.4)2
= (10)2 – 2 × 10 × 0.4 + (0.4)2 [Using, (a – b)2 = a2 – 2ab + b2]
= 100 – 8.0 + 0.16
= 92.16
Question 3. Find the following squares, using the identities:
(i) (pq + 5r)2
(ii) (5a/2 – 3b/5)2
(iii) (√2a + √3b)2
(iv) (2x/3y – 3y/2x)2
Answer:
(i) (pq + 5r)2
= (pq)2 + 2 × pq × 5r + (5r)2 [Using, (a + b)2 = a2 + 2ab + b2]
= p2q2 + 10pqr + 25r2
(ii) (5a/2 – 3b/5)2
= (5a/2)2 – 2 × (5a/2) × (-3b/5) + (3b/5)2 [Using, (a – b)2 = a2 – 2ab + b2]
= 25a2/4 – 3ab + 9b2/25
(iii) (√2a + √3b)2
= (√2a)2 + 2 × √2a × √3b + (√3b)2 [Using, (a + b)2 = a2 + 2ab + b2]
= 2a2 + 2√6ab + 3b2
(iv) (2x/3y – 3y/2x)2
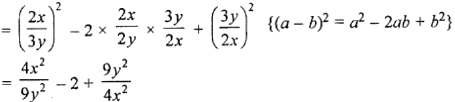
Question 4. Using the identity, (x + a) (x + b) = x2 + (a + b)x + ab, find the following products:
(i) (x + 7) (x + 3)
(ii) (3x + 4) (3x – 5)
(iii) (p2 + 2q) (p2 – 3q)
(iv) (abc + 3) (abc – 5)
Answer:
(i) (x + 7) (x + 3)
= (x)2 + (7 + 3)x + 7 × 3
= x2 + 10x + 21
(ii) (3x + 4) (3x – 5)
= (3x)2 + (4 – 5) (3x) + 4 × (-5)
= 9x2 – 3x – 20
(iii) (P2 + 2q)(p2 – 3q)
= (p2)2 + (2q – 3q)p2 + 2q × (-3q)
= p4 – p2q – 6pq
(iv) (abc + 3) (abc – 5)
= (abc)2 + (3 – 5)abc + 3 × (-5)
= a2b2c2 – 2abc – 15
Question 5. Using the identity, (x + a) (x + b) = x2 + (a + b)x + ab, evaluate the following:
(i) 203 × 204
(ii) 8.2 × 8.7
(iii) 107 × 93
Answer:
(i) 203 × 204
= (200 + 3) (200 + 4)
= (200)2 + (3 + 4) × 200 + 3 × 4
= 40000 + 1400 + 12
= 41412
(ii) 8.2 × 8.7
= (8 + 0.2) (8 + 0.7)
= (8)2 + (0.2 + 0.7) × 8 + 0.2 × 0.7
= 64 + 8 × (0.9) + 0.14
= 64 + 7.2 + 0.14
= 71.34
(iii) 107 × 93
= (100 + 7) (100 – 7)
= (100)2 + (7 – 7) × 100 + 7 × (-7)
= 10000 + 0 – 49
= 9951
Question 6. Using the identity a2 – b2 = (a + b) (a – b), find
(i) 532 – 472
(ii) (2.05)2 – (0.95)2
(iii) (14.3)2 – (5.7)2
Answer:
(i) 532 – 472
= (50 + 3) (50 – 3)
= (50)2 – (3)2
= 2500 – 9
= 2491
(ii) (2.05)2 – (0.95)2
= (2.05 + 0.95) (2.05 – 0.95)
= 3 × 1.10
= 3.3
(iii) (14.3)2 – (5.7)2
= (14.3 + 5.7) (14.3 – 5.7)
= 20 × 8.6
= 172
Question 7. Simplify the following:
(i) (2x + 5y)2 + (2x – 5y)2
(ii) (7a/2 – 5b/2)2 – (5a/2 – 7b/2)2
(iii) (p2 – q2r)2 + 2p2q2r
Answer:
(i) (2x + 5y)2 + (2x – 5y)2 [Using, (a ± b)2 = a2 ± 2ab + b2]
= (2x)2 + 2 × 2x × 5y + (5y)2 + (2x)2 – 2 × 2x × 5y + (5y)2
= 4x2 + 20xy + 25y2 + 4x2 – 20xy + 25y2
= 8x2 + 50y2
(ii) (7a/2 – 5b/2)2 – (5a/2 – 7b/2)2
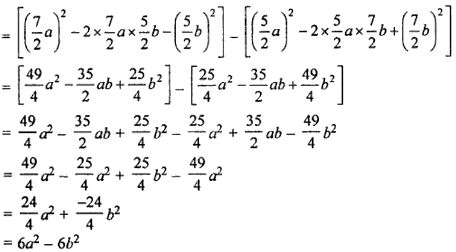
(iii) (p2 – q2r)2 + 2p2q2r [Using, (a – b)2 = a2 – 2ab + b2]
= (p2)2 – 2 × p2 × q2r + (q2r)2 + 2p2q2r
= p4 – 2p2q + q4r2 + 2p2q2r
= p4 + q4r2
Question 8. show that:
(i) (4x + 7y)2 – (4x – 7y)2 = 112xy
(ii) (3p/7 – 7q/6)2 + pq = 9p2/49 + 49q2/36
(iii) (p – q)(p + q) + (q – r)(q + r) + (r – p) (r + p) = 0
Answer:
(i) Taking LHS, e
LHS = (4x + 7y)2 – (4x – 7y)2 [Using, (a ± b)2 = a2 ± 2ab + b2]
= [(4x)2 + 2 × 4x × 7y + (7y)2] – [(4x)2 – 2 × 4x + 7y + (7y)2]
= (16x2 + 56xy + 49y2) – (16x2 – 56xy + 49y2)
= l6x2 + 56xy + 49y2 – 16x2 + 56xy – 49y2
= 112xy = RHS
(ii) Taking LHS,
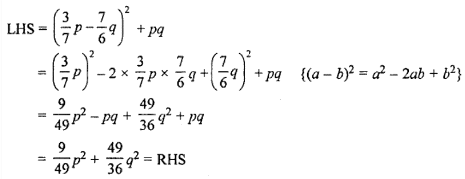
(iii) Taking LHS,
LHS = (p – q) (p + q) + (q – r) (q + r) + (r – p)(r + p)
= p2 – q2 + q2 – r2 + r2 – p2 [Using, (a + b) (a – b) = a2 – b2]
= 0 = RHS
Algebraic Expression and Identities Exe-10.5
ML Aggarwal Class 8 ICSE Maths Solutions
Page-186
Question 9. If x – 1/x = 7, evaluate:
(i) x2 + 1/x2
(ii) x4 + 1/x4
Answer:
x – 1/x = 7
On squaring on both sides, we get
(x – 1/x)2 = 72
x2 – 2 × x2 × 1/x2 + 1/x2 = 49
x2 – 2 + 1/x2 = 49
x2 + 1/x2 = 49 + 2
Hence,
x2 + 1/x2 = 51
(ii) Again squaring,
(x2 + 1/x2)2 = 512
x4 + 1/x4 + 2 × x2 × 1/x2 = 2601
x4 + 1/x4 + 2 = 2601
x4 + 1/x4 = 2601 – 2
Hence,
x4 + 1/x4 = 2599
Question 10. If x2 + 1/x2 = 23, evaluate:
(i) x + 1/x
(ii) x – 1/x
Answer:
x2 + 1/x2 = 23
(i) (x + 1/x)2 = x2 + 1/x2 + 2
= 23 + 2
= 25
Taking square root on both sides, we get
(x + 1/x) = ±5
Hence, x + 1/x = 5 or -5
(ii) (x – 1/x)2 = x2 + 1/x2 – 2
= 23 – 2
= 21
Taking square root on both sides, we get
(x + 1/x) = ±√21
Hence, x + 1/x = √21 or -√21
Question 11. If a + b = 9 and = 10, find the value of a2 + b2.
Answer:
a + b = 9 and ab = 10
Now, squaring a + b = 9 on both sides, we have
(a + b)2 = (9)
a2 + b2 + 2ab = 81
a2 + b2 + 2 × 10 = 81
a2 + b2 + 20 = 81
a2 + b2 = 81 – 20 = 61
∴ a2 + b2 = 61
Question 12. If a – b = 6 and a2 + b2 = 42, find the value of
Answer:
a – b = 6 and a2 + b2 = 42
a – b = 6
Now, squaring a – b = 6 on both sides, we have
(a – b)2 = (6)2
a2 + b2 – 2ab = 36
42 – 2ab = 36
2ab = 42 – 36 = 6
ab = 6/2 = 3
∴ ab = 3
(ML Aggarwal Algebraic Expression and Identities Exe-10.5 Class 8)
Question 13. If a2 + b2 = 41 and ab = 4, find the values of
(i) a + b
(ii) a – b
Answer:
a2 + b2 = 41 and ab = 4
(i) (a + b)2 = a2 + b2 + 2ab
= 41 + 2 × 4
= 41 + 8
= 49
∴ a + b = ±7
(ii) (a – b)2 = a2 + b2 – 2ab
= 41 – 2 × 4
= 41 – 8
= 33
∴ a – b = ±√33
— End of Algebraic Expression and Identities Exe-10.5 Class 8 ICSE Maths Solutions :–
Return to : – ML Aggarwal Maths Solutions for ICSE Class -8
Thanks



RS and ML are brothers?? Please tell
No