ML Aggarwal Direct and Inverse Variation Check Your Progress Class 8 ICSE Ch-9 Maths Solutions. We Provide Step by Step Answer of Check Your Progress Questions for Direct and Inverse Variation as council prescribe guideline for upcoming board exam. Visit official Website CISCE for detail information about ICSE Board Class-8.
ML Aggarwal Direct and Inverse Variation Check Your Progress Class 8 ICSE Maths Solutions
| Board | ICSE |
| Publications | Avichal Publishig Company (APC) |
| Subject | Maths |
| Class | 8th |
| Chapter-9 | Direct and Inverse Variation |
| Writer | ML Aggarwal |
| Book Name | Understanding |
| Topics | Solution of Check Your Progress Questions |
| Edition | 2023-2024 |
Direct and Inverse Variation Check Your Progress
ML Aggarwal Class 8 ICSE Maths Solutions
Page-164
Question 1. Match each of the entries in column I with the appropriate entry in column II.
| Column 1 | Column 2 |
| (i) x and y vary inversely each other | (a) x/y= constant |
| (ii) Mathematical representation of direct variation of quantities m and n | (b) y will increase in proportion. |
| (iii) Mathematical representation of inverse variation of quantities p and q | (c) x y = constant |
| (iv) If x and y vary inversely then on decreasing x. | (d) p ∝ 1/q |
| (v) x and y vary directly to each other. | (e) y will decrease in proportion |
| (vi) If x and y vary directly then on decreasing x. | (f) m ∝ n |
Answer:
| Column 1 | Column 2 |
| (i) x and y vary inversely each other | (c) x y = constant |
| (ii) Mathematical representation of direct variation of quantities m and n | (f) m ∝ n |
| (iii) Mathematical representation of inverse variation of quantities p and q | (d) p ∝ 1/q |
| (iv) If x and y vary inversely then on decreasing x. | (b) y will increase in proportion. |
| (v) x and y vary directly to each other. | (a) x/y = constant |
| (vi) If x and y vary directly then on decreasing x. | (e) y will decrease in proportion |
Direct and Inverse Variation Check Your Progress
ML Aggarwal Class 8 ICSE Maths Solutions
Page-165
Question 2.
(i) From the following table, determines and q if x and y vary directly:
| x | 6 | p | 15 | 20 | 25 |
| y | 18 | 27 | q | 60 | 75 |
(ii) From the following table, determine a and b if x and y vary inversely:
| x | 2 | a | 6 | 10 |
| y | 45 | 12.5 | b | 9 |
Answer:
(i)
| x | 6 | p | 15 | 20 | 25 |
| y | 18 | 27 | q | 60 | 75 |
Since x/y = y/16 = 1/3, 25/75 = 1/3
Therefore it is direct variation.
Now,p/27=1/3 p=27/3=9
15/q=1/3 q=15*3=45
Therefore p=9 ,q=45.
(ii)
| x | 2 | a | 6 | 10 | |
| y | 45 | 12.5 | b | 9 |
x y = 28 45 =90, 10*9 =90
Therefore x y are inverse variation .
therefore a* 12.5= a=90/12.5
=90*10/125
a = 36/5=7.2
6*b=90 b=90/6=15/
Therefore a =7.2 , b = 15
Question 3. It rained 80 mm in the first 20 days of April. What would be the total rainfall in April?
Answer:
rained 80 min in first 20 days of April
We cant calculate the total rainfall in April
As there is no info. about the rest 10 days
Question 4. Mamta earns ₹540 for a working week of 48 hours. If she was absent for 6 hours, how much did she earn?
Answer:
Mamta earn Rs. 540 for working week of 48 hrs.
Let mamta earn Rs. x for a working week of 42 hrs.
| No. of 80 hrs. | 48 | 42 |
| Cost | 540 | 8 |
Therefore it is direct variation
48/540= 42/x
x=42*540/48 = 472.50
Hence Mamta earns Rs. 472.50 for a working week of 42 hrs.
Question 5. Navjot can do a piece of work in 6 days working 10 hours per day. In how many days can he do the same work if he increases his working hours by 2 hours per day?
Answer:
Working hrs per day =10
Therefore working hours in 6 days =6*10=60
When increase the working hrs. by 2 hrs per day
Then new working hrs =10+2=12
Hence no. of days to complete the work =60/12 =5 days
Question 6. Sharmila has enough money to buy 24 bananas at the rate of ₹ 1·50 per banana. How many bananas she can buy if the price of each orange is decreased by 30 paise?
Answer:
Amt. of money to buy 24 bananas at the rate of Rs. 1.50 per banana = Rs. 24*1.50 =Rs. 36
When price of each banana is decreased by 30 paise
=Rs.(1.50-0.30) =Rs 1.20
In Rs. 1.20 buy 1 banana
Therefore in Rs. 1 buy =1/1.20 banana
Therefore in Rs. 36 buy =36/1.20 bananas
That is 30 bananas
Hence sharmila can buy 30 bananas .
Question 7. A fort has rations for 180 soldiers for 40 days. After 10 days, 30 soldiers leave the fort. Find the total number of days for which the food will last.
Answer :
No. of soldiers in the beginning=180
No. soldiers left=30
Therefore No. of soldiers now =180-130=150
No. of total days =40
No. of days passed = 10
Therefore No. of days left=40-10=30
Now , for 180 soldiers the ratio will be for =30*180/150=36 days
Therefore total period =36+10=46 days
Question 8. There are 100 students in a hostel. Food provision for them is for 20 days. How long will these provisions last, if 25 more students join the group?
Answer:
In a hostel there are 100 students and food is sufficient for 20 days by joining 25 more students
The no. of students now =100+25 =125
100:125=20 days : x
More students less days
Therefore by inverse variation
125:100=20:x
x= 100*20/125=16
The food will be sufficient for 16 days
Question 9. If 4 goats or 6 sheep can graze a field in 40 days, how many days will 4 goats and 14 sheep take to graze the same field?
Answer:
Since 4 goats work=6 sheep’s work
Therefore 4 goats and 14 sheep’s work=(6+14) sheeps work
=20 sheep’s work
Therefore 6 sheep’s can graze a field in 40 days
Therefore 1 sheep can graze a field in 6*40 days
20 Sheep can graze a field in
6*40/20 days = 12 days
Question 10. A tap can fill a tank in 20 hours, while the other can empty it in 30 hours. The tank is empty and if both taps are opened together, how long will it take for the tank to be half full?
Answer:
tank filled in 1 hour =1÷20
tank emptied in 1 hour =1÷30
if both taps are opened together then it will filled in =1÷20 – 1÷30
=3-2÷60
=1÷60
=60 Answer
but it has asked Half
so,
it will be 60/2
=30 Answer.
Question 11. Three ants separately can gobble a grasshopper in 3,4, and 6 days respectively. How many days will they take together to finish off the poor chap? If the grasshopper weighs 63 gram, find the share of each.
Answer:
Update soon.
Question 12. A and B together can do a piece of work in 12 days; B and C together can do it in 15 days. If A is twice as good a workman as C, in how many days A alone will do the same work?
Answer:
Let one days word of A = 1/a
One days word of B = 1/b
One days word of C = 1/c
A and B can do a piece of work in 12 days.
(1/a) + (1/b) = 1/12 …. (1)
B and C together can do it in 15 days.
(1/b) +(1/c) = 1/15 …. (2)
A is twice as good a workman as C.
(1/a) 2x(1/c)
From (1) and (2) substitute the values of 1/a and 1/c.
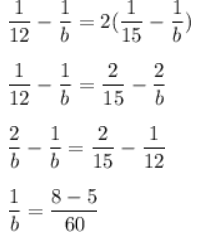
(1/b) = (1/20)
b = 20
Therefore, B alone can do it in 20 days.
— End of Direct and Inverse Variation Check Your Progress Class 8 ICSE Maths Solutions :–
Return to : – ML Aggarwal Maths Solutions for ICSE Class -8
Thanks


