ML Aggarwal Expansions Exe-3.2 Class 9 ICSE Maths Solutions

ML Aggarwal Expansions Exe-3.2 Class 9 ICSE Maths Solutions . We Provide Step by Step Answer of  Exe-3.2 Questions as council prescribe guideline for upcoming exam. Visit official website CISCE for detail information about ICSE Board Class-9.

ML Aggarwal Expansions Exe-3.2 Class 9 ICSE Maths Solutions

Board	ICSE
Subject	Maths
Class	9th
Chapter-3	Expansions
Topics	Solution of Exe-3.2 Questions
Edition	2024-2025

Problems on Expansion

ML Aggarwal Expansions Exe-3.2 Class 9 ICSE Maths Solutions

Question 1. If x – y = 8 and xy = 5, find x² + y².

Answer :

We know that

(x – y)² = x² + y² – 2xy

It can be written as

x² + y² = (x – y)² + 2xy

It is given that

x – y = 8 and xy = 5

Substituting the values

x² + y² = 8² + 2 × 5

So we get

= 64 + 10

= 74

Question 2. If x + y = 10 and xy = 21, find 2 (x² + y²).

Answer :

We know that

(x + y)² = x² + y² + 2xy

It can be written as

x² + y² = (x + y)² – 2xy

It is given that

(x + y) = 10 and xy = 21

Substituting the values

x² + y² = 10² – 2 × 21

By further calculation

= 100 – 42

= 58

Here

2 (x² + y²) = 2 × 58 = 116

Question 3. If 2a + 3b = 7 and ab = 2, find 4a² + 9b².

Answer :

We know that

(2a + 3b)² = 4a² + 9b² + 12ab

It can be written as

4a² + 9b² = (2a + 3b)² – 12ab

It is given that

2a + 3b = 7

ab = 2

Substituting the values

4a² + 9b² = 7² – 12 × 2

By further calculation

= 49 – 24

= 25

Question 4. If 3x – 4y = 16 and xy = 4, find the value of 9x² + 16y².

Answer :

We know that

(3x – 4y)² = 9x² + 16y² – 24xy

It can be written as

9x² + 16y² = (3x – 4y)² + 24xy

It is given that

3x – 4y = 16 and xy = 4

Substituting the values

9x² + 16y² = 16² + 24 × 4

By further calculation

= 256 + 96

= 352

Question 5. If x + y = 8 and x – y = 2, find the value of 2x² + 2y².

Answer :

We know that

2 (x² + y²) = (x + y)² + (x – y)²

It is given that

x + y = 8 and x – y = 2

Substituting the values

2x² + 2y² = 8² + 2²

By further calculation

= 64 + 4

= 68

Question 6. If a² + b² = 13 and ab = 6, find

(i) a + b

(ii) a – b

Answer :

(i) We know that

(a + b)² = a² + b² + 2ab

Substituting the values

= 13 + 2 × 6

So we get

= 13 + 12

= 25

Here

a + b = ± √25 = ± 5

(ii) We know that

(a – b)² = a² + b² – 2ab

Substituting the values

= 13 – 2 × 6

So we get

= 13 – 12

= 1

Here

a – b = ± √1 = ± 1

Question 7. If a + b = 4 and ab = -12, find

(i) a – b

(ii) a² – b².

Answer :

(i) We know that

(a – b)² = a² + b² – 2ab

It can be written as

(a – b)² = a² + b² + 2ab – 4ab

(a – b)² = (a + b)² – 4ab

It is given that

a + b = 4 and ab = – 12

Substituting the values

(a – b)² = 4² – 4 (-12)

By further calculation

(a – b)² = 16 + 48 = 64

So we get

(a – b) = ± √64 = ± 8

(ii) We know that

a² – b² = (a + b) (a – b)

Substituting the values

a² – b² = 4 × ±8

a² – b² = ± 32

Question 8. If p – q = 9 and pq = 36, evaluate

(i) p + q

(ii) p² – q².

Answer :

(i) We know that

(p + q)² = p² + q² + 2pq

It can be written as

(p + q)² = p² + q² – 2pq + 4pq

(p + q)² = (p – q)² + 4pq

It is given that

p – q = 9 and pq = 36

Substituting the values

(p + q)² = 9² + 4 × 36

By further calculation

(p + q)² = 81 + 144 = 225

So we get

p + q = ± √225 = ± 15

(ii) We know that

p² – q² = (p – q) (p + q)

Substituting the values

p² – q² = 9 ×±15

p² – q² = ± 135

Question 9. If x + y = 6 and x – y = 4, find

(i) x² + y²

(ii) xy

Answer :

We know that

(x + y)² – (x – y)² = 4xy

Substituting the values

6² – 4² = 4xy

By further calculation

36 – 16 = 4xy

20 = 4xy

4xy = 20

So we get

xy = 20/4 = 5

(i) x² + y² = (x + y)² – 2xy

Substituting the values

= 6² – 2 × 5

By further calculation

= 36 – 10

= 26

(ii) xy = 5

Question 10. If x – 3 = 1/x, find the value of x² + 1/x².

Answer :

It is given that

x – 3 = 1/x

We can write it as

x – 1/x = 3

Here

(x – 1/x)² = x² + 1/x² – 2

So we get

x² + 1/x² = (x – 1/x)² + 2

Substituting the values

x² + 1/x² = 3² + 2

By further calculation

= 9 + 2

= 11

Question 11. If x + y = 8 and xy = 3 ¾, find the values of

(i) x – y

(ii) 3 (x² + y²)

(iii) 5 (x² + y²) + 4 (x – y).

Answer :

(i) We know that

(x – y)² = x² + y² – 2xy

It can be written as

(x – y)² = x² + y² + 2xy – 4xy

(x – y)² = (x + y)² – 4xy

It is given that

x + y = 8 and xy = 3 ¾ = 15/4

Substituting the values

(x – y)² = 8² – 4 × 15/4

So we get

(x – y)² = 64 – 15 = 49

x – y = ± √49 = ± 7

(ii) We know that

(x + y)² = x² + y² + 2xy

We can write it as

x² + y² = (x + y)² – 2xy

It is given that

x + y = 8 and xy = 3 ¾ = 15/4

Substituting the values

x² + y² = 8² – 2 × 15/4

So we get

x² + y² = 64 – 15/2

Taking LCM

x² + y² = (128 – 15)/ 2 = 113/2

We get

3 (x² + y²) = 3 × 113/2 = 339/2 = 169 ½

(iii) We know that

5 (x² + y²) + 4 (x – y) = 5 × 113/2 + 4 × ± 7

By further calculation

= 565/2 ± 28

We can write it as

= 565/2 + 28 or 565/2 – 28

= 621/2 or 509/2

It can be written as

= 310 ½ or 254 ½

Question 12. If x² + y² = 34 and xy = 10 ½, find the value of 2 (x + y)² + (x – y)².

Answer:

It is given that

x² + y² = 34 and xy = 10 ½ = 21/2

We know that

(x + y)² = x² + y² + 2xy

Substituting the values

(x + y)² = 34 + 2 (21/2)

So we get

(x + y)² = 55 ….. (1)

We know that

(x – y)² = x² + y² – 2xy

Substituting the values

(x – y)² = 34 – 2 (21/2)

So we get

(x – y)² = 34 – 21 = 13 ….. (2)

Using both the equations

2 (x + y)² + (x – y)² = 2 × 55 + 13 = 123

Question 13. If a – b = 3 and ab = 4, find a³ – b³.

Answer :

We know that

a³ – b³ = (a – b)³ + 3ab (a + b)

Substituting the values

a³ – b³ = 3³ + 3 × 4 × 3

By further calculation

a³ – b³ = 27 + 36 = 63

Question 14. If 2a – 3b = 3 and ab = 2, find the value of 8a³ – 27b³.

Answer :

We know that

8a³ – 27b³ = (2a)³ – (3b)³

According to the formula

= (2a – 3b)³ + 3 × 2a × 3b (2a – 3b)

By further simplification

= (2a – 3b)³ + 18ab (2a – 3b)

Substituting the values

= 3³ + 18 × 2 × 3

By further calculation

= 27 + 108

= 135

Question 15. If x + 1/x = 4, find the values of

(i) x² + 1/x²

(ii) x⁴ + 1/x⁴

(iii) x³ + 1/x³

(iv) x – 1/x.

Answer :

(i) We know that

(x + 1/x)² = x² + 1/x² + 2

It can be written as

x² + 1/x² = (x + 1/x)² – 2

Substituting the values

= 4² – 2

= 16 – 2

= 14

(ii) We know that

(x² + 1/x²)² = x⁴ + 1/x⁴ + 2

It can be written as

x⁴ + 1/x⁴ = (x² + 1/x²)² – 2

Substituting the values

= 14² – 2

= 196 – 2

= 194

(iii) We know that

x³ + 1/x³ = (x + 1/x)³ – 3x (1/x) (x + 1/x)

It can be written as

(x + 1/x)³ – 3(x + 1/x) = 4³ – 3 × 4

By further calculation

= 64 – 12

= 52

(iv) We know that

(x – 1/x)² = x² + 1/x² – 2

Substituting the values

= 14 – 2

= 12

So we get

x – 1/x = ± 2√3

Question 16. If x – 1/x = 5, find the value of x⁴ + 1/x⁴.

Answer :

We know that

(x – 1/x)² = x² + 1/x² – 2

It can be written as

x² + 1/x² = (x – 1/x)² + 2

Substituting the values

x² + 1/x² = 5² + 2 = 27

Here

x⁴ + 1/x⁴ = (x² + 1/x²)² – 2

Substituting the values

x⁴ + 1/x⁴ = 27² – 2

So we get

= 729 – 2

= 727

Question 17. If x – 1/x = √5, find the values of

(i) x² + 1/x²

(ii) x + 1/x

(iii) x³ + 1/x³

Answer :

(i) x² + 1/x² = (x – 1/x)² + 2

Substituting the values

= (√5)² + 2

= 5 + 2

= 7

(ii) (x + 1/x)² = x² + 1/x² + 2

Substituting the values

= 7 + 2

= 9

Here

(x + 1/x)² = 9

So we get

(x + 1/x) = ± √9 = ± 3

(iii) x³ + 1/x³ = (x + 1/x)³ – 3x (1/x) (x + 1/x)

Substituting the values

= (± 3)³ – 3 (± 3)

By further calculation

= (± 27) – (± 9)

= ± 18

Question 18. If x + 1/x = 6, find

(i) x – 1/x

(ii) x² – 1/x².

Answer :

(i) We know that

(x – 1/x)² = x² + 1/x² – 2

It can be written as

(x – 1/x)² = x² + 1/x² + 2 – 4

(x – 1/x)² = (x + 1/x)² – 4

Substituting the values

(x – 1/x)² = 6² – 4 = 32

So we get

x – 1/x = ± √32 = ± 4√2

(ii) We know that

x² – 1/x² = (x – 1/x) (x + 1/x)

Substituting the values

x² – 1/x² = (± 4√2) (6) = ± 24 √2

Question 19. If x + 1/x = 2, prove that x² + 1/x² = x³ + 1/x³ = x⁴ + 1/x⁴.

Answer :

We know that

x² + 1/x² = (x + 1/x)² – 2

Substituting the values

x² + 1/x² = 2² – 2

So we get

x² + 1/x² = 4 – 2 = 2 …. (1)

x³ + 1/x³ = (x + 1/x)³ – 3 (x + 1/x)

Substituting the values

x³ + 1/x³ = 2³ – 3 × 2

So we get

x³ + 1/x³ = 8 – 6 = 2 …… (2)

x⁴ + 1/x⁴ = (x² + 1/x²)² – 2

Substituting the values

x⁴ + 1/x⁴ = 2² – 2

So we get

x⁴ + 1/x⁴ = 4 – 2 = 2 …. (3)

From equation (1), (2) and (3)

x² + 1/x² = x³ + 1/x³ = x⁴ + 1/x⁴

Hence, it is proved.

Question 20. If x – 2/x = 3, find the value of x³ – 8/x³.

Answer:

We know that

(x – 2/x)³ = x³ – 8/x³ – 3 (x) (2/x) (x – 2/x)

By further simplification

(x – 2/x)³ = x³ – 8/x³ – 6 (x – 2/x)

It can be written as

x³ – 8/x³ = (x – 2/x)³ + 6 (x – 2/x)

Substituting the values

x³ – 8/x³ = 3³ + 6 × 3

By further calculation

x³ – 8/x³ = 27 + 18 = 45

Question 21. If a + 2b = 5, prove that a³ + 8b³ + 30ab = 125.

Answer :

We know that

(a + 2b)³ = a³ + 8b³ + 3 (a) (2b) (a + 2b)

Substituting the values

5³ = a³ + 8b³ + 6ab (5)

By further calculation

125 = a³ + 8b³ + 30ab

Therefore, a³ + 8b³ + 30ab = 125.

---

Page 85

Question 22. If a + 1/a = p, prove that a³ + 1/a³ = p (p² – 3).

Answer :

We know that

a³ + 1/a³ = (a + 1/a)³ – 3a (1/a) (a + 1/a)

Substituting the values

a³ + 1/a³ = p³ – 3p

Taking p as common

a³ + 1/a³ = p (p² – 3)

Therefore, it is proved.

Question 23. If x² + 1/x² = 27, find the value of x – 1/x.

Answer :

We know that

(x – 1/x)² = x² + 1/x² – 2

Substituting the values

(x – 1/x)² = 27 – 2 = 25

So we get

x – 1/x = ± √25 = ± 5

Question 24. If x² + 1/x² = 27, find the value of 3x³ + 5x – 3/x³ – 5/x.

Answer :

We know that

(x – 1/x)² = x² + 1/x² – 2

Substituting the values

(x – 1/x)² = 27 – 2 = 25

So we get

x – 1/x = ± √25 = ± 5

Here

3x³ + 5x – 3/x³ – 5/x = 3 (x³ – 1/x³) + 5 (x – 1/x)

It can be written as

= 3 [(x – 1/x)³ + 3 (x – 1/x)] + 5 (x – 1/x)

Substituting the values

= 3 [(± 5)³ + 3 (± 5)] + 5 (± 5)

By further calculation

= 3 [(± 125) + (± 15)] + (± 25)

So we get

= (± 375) + (± 45) + (± 25)

= ± 445

Question 25. If x² + 1/25x² = 8 3/5, find x + 1/5x.

Answer :

We know that

(x + 1/5x)² = x² + 1/25x² + 2x (1/5x)

It can be written as

(x + 1/5x)² = x² + 1/25x² + 2/5

Substituting the values

(x + 1/5x)² = 8 3/5 + 2/5

(x + 1/5x)² = 43/5 + 2/5

So we get

(x + 1/5x)² = 45/5 = 9

Here

x + 1/5x = ± √9 = ± 3

Question 26. If x² + 1/4x² = 8, find x³ + 1/8x³.

Answer :

We know that

(x + 1/2x)² = x² + (1/2x)² + 2x (1/2x)

It can be written as

(x + 1/2x)² = x² + 1/4x² + 1

Substituting the values

(x + 1/2x)² = 8 + 1 = 9

So we get

x + 1/2x = ± √9 = ± 3

Here

x³ + 1/8x³ = x³ + (1/2x)³

We know that

x³ + 1/8x³ = (x + 1/2x)³ – 3x (1/2x) (x + 1/2x)

Substituting the values

x³ + 1/8x³ = (± 3)³ – 3/2 (± 3)

By further calculation

x³ + 1/8x³ = ± (27 – 9/2)

Taking LCM

x³ + 1/8x³ = ± (54 – 9)/ 2

x³ + 1/8x³ = ± 45/2 = ± 22 ½

Therefore, x³ + 1/8x³ = ± 22 ½.

Question 27. If a² – 3a + 1 = 0, find

(i) a² + 1/a²

(ii) a³ + 1/a³.

Answer :

It is given that

a² – 3a + 1 = 0

By dividing each term by a

a + 1/a = 3

(i) We know that

(a + 1/a)² = a² + 1/a² + 2

It can be written as

a² + 1/a² = (a + 1/a)² – 2

Substituting the values

= 3² – 2

= 9 – 2

= 7

(ii) We know that

(a + 1/a)³ = a³ + 1/a³ + 3 (a + 1/a)

It can be written as

a³ + 1/a³ = (a + 1/a)³ – 3 (a + 1/a)

Substituting the values

= 3³ – 3 (3)

= 27 – 9

= 18

Question 28. If a = 1/ (a – 5), find

(i) a – 1/a

(ii) a + 1/a

(iii) a² – 1/a².

Answer :

It is given that

a = 1/ (a – 5)

We can write it as

a² – 5a – 1 = 0

Now divide each term by a

a – 5 – 1/a = 0

So we get

a – 1/a = 5

(i) a – 1/a = 5

(ii) We know that

(a + 1/a)² = (a – 1/a)² + 4

Substituting the values

(a + 1/a)² = 5² + 4

So we get

(a + 1/a)² = 25 + 4 = 29

a + 1/a = ± √29

(iii) We know that

a² – 1/a² = (a + 1/a) (a – 1/a)

Substituting the values

a² – 1/a² = ± √29 × 5

a² – 1/a² = ± 5√29

Question 29. If (x + 1/x)² = 3, find x³ + 1/x³.

Answer :

It is given that

(x + 1/x)² = 3

(x + 1/x) = ± √3

We know that

x³ + 1/x³ = (x + 1/x)³ – 3 (x + 1/x)

Substituting the values

x³ + 1/x³ = (± √3)³ – 3 (± √3)

By further calculation

x³ + 1/x³ = (± 3√3) – (± 3√3) = 0

Question 30. If x = 5 – 2√6, find the value of √x + 1/√x.

Answer :

It is given that

x = 5 – 2√6

We can write it as

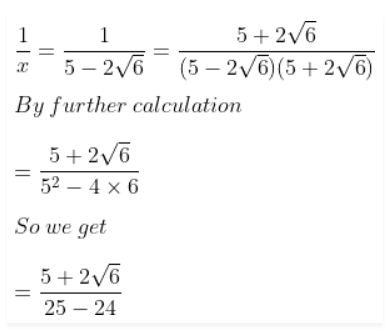
= 5 + 2√6

Here

x + 1/x = 5 – 2√6 + 5 + 2√6 = 10

So we get

(√x + 1/√x)² = x + 1/x + 2

Substituting the values

= 10 + 2

= 12

Question 31. If a + b + c = 12 and ab + bc + ca = 22, find a² + b² + c².

Answer :

We know that

(a + b + c)² = a² + b² + c² + 2(ab + bc + ca)

We can write it as

a² + b² + c² = (a + b + c)² – 2 (ab + bc + ca)

Substituting the values

a² + b² + c² = 12² – 2 (22)

By further calculation

a² + b² + c² = 144 – 44 = 100

Question 32. If a + b + c = 12 and a² + b² + c² = 100, find ab + bc + ca.

Answer :

We know that

(a + b + c)² = a² + b² + c² + 2ab + 2bc + 2ca

It can be written as

2ab + 2bc + 2ca = (a + b + c)² – (a² + b² + c²)

Taking out 2 as common

2 (ab + bc + ca) = 12² – 100 = 144 – 100 = 44

By further calculation

ab + bc + ca = 44/2 = 22

Question 33. If a² + b² + c² = 125 and ab + bc + ca = 50, find a + b + c.

Answer :

We know that

(a + b + c)² = a² + b² + c² + 2(ab + bc + ca)

Substituting the values

(a + b + c)² = 125 + 2 (50)

By further calculation

(a + b + c)² = 125 + 100 = 225

So we get

a + b + c = ± √225 = ± 15

Question 34. If a + b – c = 5 and a² + b² + c² = 29, find the value of ab – bc – ca.

Answer :

It is given that

a + b – c = 5

By squaring on both sides

(a + b – c)² = 5²

Expanding using formula

a² + b² + c² + 2ab – 2bc – 2ca = 25

Substituting the values and taking 2 as common

29 + 2 (ab – bc – ca) = 25

By further calculation

2 (ab – bc – ca) = 25 – 29 = – 4

So we get

ab – bc – ca = – 4/2 = – 2

Therefore, ab – bc – ca = – 2.

Question 35. If a – b = 7 and a² + b² = 85, then find the value of a³ – b³.

Answer :

We know that

(a – b)² = a² + b² – 2ab

Substituting the values

7² = 85 – 2ab

By further calculation

49 = 85 – 2ab

So we get

2ab = 85 – 49 = 36

Dividing by 2

ab = 36/2 = 18

Here

a³ – b³ = (a – b) (a² + b² + ab)

Substituting the values

a³ – b³ = 7 (85 + 18)

By further calculation

a³ – b³ = 7 × 103

So we get

a³ – b³ = 721

Question 36. If the number x is 3 less than the number y and the sum of the squares of x and y is 29, find the product of x and y.

Answer :

It is given that

x = y – 3 and x² + y² = 29

It can be written as

x – y = – 3

By squaring on both sides

(x – y)² = (-3)²

Expanding using formula

x² + y² – 2xy = 9

Substituting the values

29 – 2xy = 9

By further calculation

-2xy = 9 – 29 = – 20

Dividing by 2

xy = – 20/-2 = 10

So we get

xy = 10

Question 37. If the sum and the product of two numbers are 8 and 15 respectively, find the sum of their cubes.

Answer :

Consider x and y as the two numbers

x + y = 8 and xy = 15

By cubing on both sides

(x + y)³ = 8³

Expanding using formula

x³ + y³ + 3xy (x + y) = 512

Substituting the values

x³ + y³ + 3 × 15 × 8 = 512

By further calculation

x³ + y³ + 360 = 512

So we get

x³ + y³ = 512 – 360 = 152

—  : End of ML Aggarwal Expansions Exe-3.2 Class 9 ICSE Maths Solutions :–

Return to :-  ML Aggarawal Maths Solutions for ICSE  Class-9

Thanks

Please Share with Your Friends