ML Aggarwal Factorisation Check Your Progress Class 8 ICSE Ch-11 Maths Solutions

ML Aggarwal Factorisation Check Your Progress Class 8 ICSE Ch-11 Maths Solutions. We Provide Step by Step Answer of  Check Your Progress Questions for Factorisation as council prescribe guideline for upcoming board exam. Visit official Website CISCE for detail information about ICSE Board Class-8.

ML Aggarwal Factorisation Check Your Progress Class 8 ICSE Maths Solutions

Board	ICSE
Publications	Avichal Publishig Company (APC)
Subject	Maths
Class	8th
Chapter-11	Factorisation
Writer	ML Aggarwal
Book Name	Understanding
Topics	Solution of Check Your Progress Questions
Edition	2023-2024

Factorisation Check Your Progress

ML Aggarwal Class 8 ICSE Maths Solutions

Page-202

Question 1. Find the HCF of the given polynomials:

(i) 14pq, 28p²q²
(ii) 8abc, 24ab², 12a²b

Answer:

(i) 14pq, 28p²q² (HCF of 14, 28 = 14)

HCF of 1 4pq, 28p²q² = 14pq

(ii) 8abc, 24ab², 12a²b

HCF of 8, 24, 12 = 4
HCF of 8abc, 24ab², 12a²b = 4ab

Question 2. Factorise the following:

(i) 10x² – 18x³ + 14x⁴
(ii) 5x²y + 10xyz + 15xy²
(iii) p²x² + c²x² – ac² – ap²
(iv) 15(x + y)² – 5x – 5y
(v) (ax + by)² + (ay – bx)²
(vi) ax + by + cx + bx + cy + ay
(vii) 49x² – 70xy + 25y²
(viii) 4a² + 12ab + 9b²
(ix) 49p² – 36q²
(x) 100x³ – 25xy²
(xi) x² – 2xy + y² – z²
(xii) x⁸ – y⁸
(xiii) 12x³ – 14x² – 10x
(xiv) p² – 10p + 21
(xv) 2x² – x – 6
(xvi) 6x² – 5xy – 6y²
(xvii) x² + 2xy – 99y²

Answer:

(i) 10x² – 18x³ + 14x⁴

HCF of 10, 18, 14 = 2

So, 10x² – 18x³ + 14x⁴

= 2x² (5 – 9x + 7x²)

(ii) 5x²y + 10xyz + 15xy²

HCF of 5, 10, 15 = 5

So, 5x²y + 10xyz + 15xy²

= 5xy (x + 2z + 3y)

(iii) p²x² + c²x² – ac² – ap

= p²x² – ap² + c²x² – ac²

= p²(x² – a) + c²(x² – a)

= (x² – a) (p² + c²)

(iv) 15(x + y)² – 5x – 5y

= 15(x + y)² – 5(x + y)

= 5(x + y) [3(x + y) – 1]

= 5(x + y) (3x + 3y – 1)

(v) (ax + by)² + (ay – bx)²

On expanding, we have

= a²x² + b²y² + 2abxy + a²y² + b²x² – 2abxy

= a²x² + a²y² + b²x² + b²y²

= a²(x² + y²) + b²(x² + y²)

= (x² + y²) (a² + b²)

(vi) ax + by + cx + bx + cy + ay

= ax + bx + cx + ay + by + cy [On grouping the like variables]

= x(a + b + c) + y(a + b + c)

= (a + b + c) (x + y)

(vii) 49x² – 70xy + 25y²

= (7x)² – 2 × 7x × 5y + (5y)² [∵ (a – b)² = a² – 2ab + b²]

= (7x – 5y)²

(viii) 4a² + 12ab + 9b²

= (2a)2² + 2 × 2a × 3b + (3b)² [∵ (a + b)² = a² + 2ab + b²]

= (2a + 3b)²

(ix) 49p² – 36q²

= (7p)² – (6q)²

= (7p + 6q) (7p – 6q) [∵ a² – b² = (a + b) (a – b)]

(x) 100x³ – 25xy²

= 25x(x² – y²) = 25x{(x)² – (y)²}

= 25x(x + y) (x – y)

(xi) x² – 2xy + y² – z²

= (x – y)² – (z)² [∵ a² -2ab + b² = (a – b)² and a² – b² = (a + b) (a – b)]

= (x – y + z)(x – y – z)

(xii) x⁸ – y⁸

= (x⁴)² – (y⁴)² [∵ a² – b² = (a + b)(a- b)]

= (x⁴ + y⁴) (x⁴ – y⁴)

= (x⁴ + y⁴) [(x²)² – (y²)²]

= (x⁴ + y⁴) (x² + y²) (x² – y²)

= (x⁴ + y⁴ (x² + y²) (x + y) (x – y)

(xiii) 12x³ – 14x² – 10x

= 2x(6x² – 7x – 5) [Now, as 6 × (-5) = -30 ⇒ -30 = -10 × 3 and -7 = -10 + 3]

= 2x(6x² + 3x – 10x – 5)

= 2x{3x(2x + 1) – 5(2x + 1)}

= 2x(2x + 1) (3x – 5)

(xiv) p² – 10p + 21

= p² – 3p – 7p + 21 [Now, as 21 =-3 × (-7) and -10 = -3 – 7]

= p(p – 3) – 7(p – 3)

= (p – 3)(p – 7)

(xv) 2x² – x – 6

= 2x² – 4x + 3x – 6 [Now, as -6 × 2 = -12 ⇒ -12 = -4 × 3 and -1 = -4 + 3]

= 2x (x – 2) + 3(x – 2)

= (x – 2) (2x + 3)

(xvi) 6x² – 5xy – 6y²

= 6x² – 9xy + 4xy – 6y² [Now, as 6 × (-6) = -36 ⇒ – 36 = -9 × 4 and – 5 = -9 + 4]

= 3x(2x – 3y) + 2y(2x – 3y)

= (2x – 3y) (3x + 2y)

(xvii) x² + 2xy – 99y²

= x² + 11xy – 9xy – 99y² [Now, as -99 = -11 × 9 and -2 = -11 + 9 }

= x(x + 11y) – 9y(x + 11y)

= (x + 11y) (x – 9y)

Question 3. Divide as directed:

^{(i) 15(y + 3)(y2 – 16) ÷ 5(y2 – y – 12)
(ii) (3×3 – 6×2 – 24x) ÷ (x – 4) (x + 2)
(iii) (x4 – 81) ÷ (x3 + 3×2 + 9x + 27)}

Answer:

(i) 15(y + 3)(y² – 16) ÷ 5(y² – y – 12)

y² – 16 = (y)² – (4)²

= (y + 4)(y – 4)

y² – y – 12 = y² – 4y + 3y – 12

= y(y – 4) + 3(y – 4)

= (y – 4)(y + 3)

Now,

= 3(y + 4)

(ii) (3x³ – 6x² – 24x) ÷ (x – 4) (x + 2)

3x³ – 6x² – 24x = 3x(x² – 2x – 8)

= 3x{x² – 4x + 2x – 8}

= 3x{x(x – 4) + 2(x – 4)}

= 3x(x – 4) (x + 2)

Now,

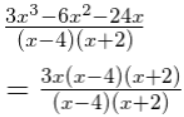
= 3x

(iii) (x⁴ – 81) ÷ (x³ + 3x² + 9x + 27)

x⁴ – 81 = (x²)² – (9)² = (x² + 9) (x² – 9)

= (x² + 9) [(x)² – (3)²]

= (x² + 9) (x + 3) (x – 3)

x³ + 3x² + 9x + 27 = (x)² + (x + 3) + 9 (x + 3)

= (x² + 9) (x + 3)

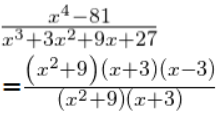
= (x – 3)

— End of Factorisation Check Your Progress Class 8 ICSE Maths Solutions :–

Return to : – ML Aggarwal Maths Solutions for ICSE Class -8

Thanks