Motion in a Plane Numerical Based on Resolution of Vectors, Laws of Vector Addition and Relative Velocity Class 11 Nootan ISC Physics Solutions Ch-5. Step by step solutions of Kumar and Mittal Physics of Nageen Prakashan as council latest prescribe guideline for upcoming exam. Visit official Website CISCE for detail information about ISC Board Class-11 Physics.

Motion in a Plane Numerical Based on Resolution of Vectors, Laws of Vector Addition and Relative Velocity
Class 11 Nootan ISC Physics Solutions Ch-5
| Board | ISC |
| Class | 11 |
| Subject | Physics |
| Writer | Kumar and Mittal |
| Publication | Nageen Prakashan |
| Chapter-5 | Motion in a Plane |
| Topics | Numerical on Resolution of Vectors, Laws of Vector Addition and Relative Velocity |
| Academic Session | 2024-2025 |
Based on Resolution of Vectors, Laws of Vector Addition and Relative Velocity
Ch-5 Motion in a Plane Class 11 Nootan ISC Physics Solutions Kumar and Mittal Physics of Nageen Prakashan
Question-1: The magnitudes of two mutually perpendicular vectors P and Q are 5 and 7 respectively. Draw a labelled vector diagram showing the magnitude and direction of →P + →Q and →P – →Q.
Answer-
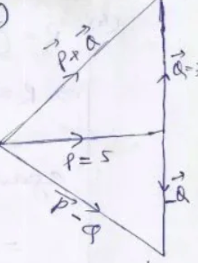
(R)² = P² + Q² + 2PQ cos 90°
=> (→P + →Q)² = 5² +7²
=>Ι →P + →QΙ = √74 = 8.6
again (→P – →Q)² = 5² + (-7)² = 74
=>Ι→P – →QΙ = √74 = 8.6
i.e. magnitude of →P +→Q and →P – →Q are same but direction are different
Question-2: A car is going towards north with a velocity 20 m/s. After some time it starts to go towards south with velocity 20 m/s. Determine change in the velocity of the car.
Answer-

Question-3: The velocity of a particle moving on a circular path is 5 cm/s towards north at any instant. After traversing one-fourth of the path its velocity is 5 cm/s towards east. Indicate the change in velocity in a vector diagram.
Answer-
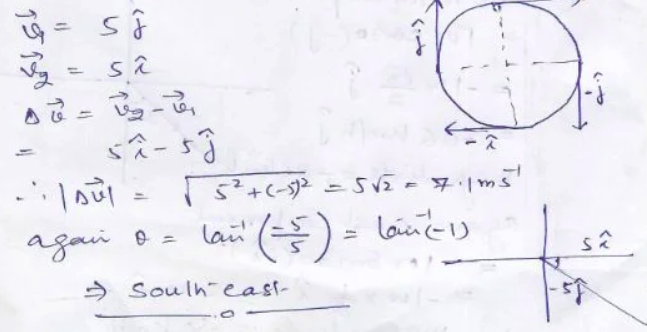
Question-4: Two forces of 6 N and 8 N act at a point at an angle of 90° with each other. Determine the magnitude and direction of the resultant force by drawing a vector diagram.
Answer-
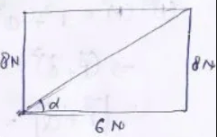
R = (P² + Q² + 2 PQ cos 90°)^1/2
R = (6² + 8² +0)^1/2 = 10N
again tan α = 8/6 = 4/3
=> tan^-1 (4/3) = 53°
Question-5: A force of 500 N is acting towards east and another of 600 N towards north. Subtract the first force from the second by drawing a vector diagram.
Answer-
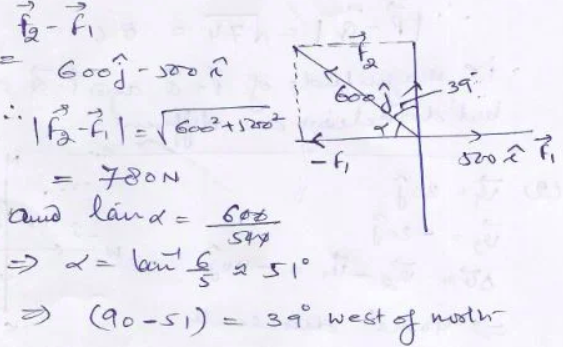
Question-6: The velocity of a body is 100 km/h, 30° west of south. Find the north and east components by drawing vector diagram.
Answer-
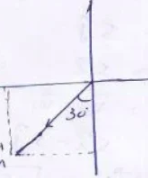
its north component
= 100 cos 30 (-ĵ )
=>-100 cos 30 ĵ
=> -100√3/2 ĵ
magnitude = -86 km/h
=> 100 sin 30 (-i)
=> -100*1/2 i
=> -50i
∴ magnitude = -50 km/h
Question-7: The handle of a grass-roller is pulled by a force of 50 N. If the handle makes an angle of 30° with the horizontal, calculate the magnitudes of the horizontal and the vertical components of the force by a vector.
Answer-

Horizontal component
= 50 cos 30 = 50 √3 /2 = 44 N
and vertical component
= 50 sin 30 = 25N
Question-8: A river flows at 3 m/s and is 300 m wide. A man swims across the river with a velocity of 2 m/s directed always perpendicular to the flow of current.
(i) How long does it take the man to cross the river?
(ii) In what direction does he actually move relative to the shore?
(iii) How far down the stream (from the starting point) does he reach the opposite bank?
Answer-
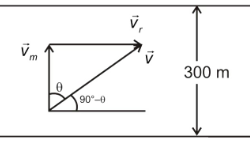
tan θ = 3/2
θ = tan^-1 (3/2) ≅ 56.3 °
Relative to shore direction is
(90° – θ) ≅ 33.7°
t = 300/v1 = 300 /2 = 150 s = 2.5 min.
x= (v11) * t
x=3*150 = 450 m
Question-9: A river flows due north with a velocity of 3.0 km/h. A man rows a boat across the river with a velocity of 4.0 km/h relative to the water due east.
(a) What is his velocity relative to the earth?
(b) If the river is 1.0 km wide, how far north of his starting point will he reach the opposite bank?
(c) How long a time is required to cross the river?
Answer-
(i) Velocity of man relative to earth will be vector sum of velocity of flow of river and velocity of boat
Magnitude v = √3²+4² = √25 = 5 km/h
Direction of v = tan^-1 (3/4) = 36.86°N of East
(ii) Here, the man moves in the east direction with 4kmph and gets simultaneously
Regards
Hence, if he travels x distance due east, in the same time he also travels 3x/4 distance due north.
Given that x=1 km, thus 3x/4= 0.75 km
(iii) The velocity of man in northward direction does not affect its speed in eastern direction which is 4km/h.
Thus time taken = distance/speed i.e. 1/4 hour = 15 min.
—: end of Motion in a Plane Numerical Based on Resolution of Vectors, Laws of Vector Addition and Relative Velocity Class 11 Nootan Physics Ch-5 :—
Return to : – Nootan Solutions for ISC Physics Class-11 Nageen Prakashan
Thanks
Please Share with your friends if helpful


