Numerical on Distance Displacement Velocity Acceleration Graph Class 11 Physics ISC Nootan Solutions Ch-4 Motion in a Straight Line. Step by step solutions of Kumar and Mittal Physics of Nageen Prakashan as council latest prescribe guideline for upcoming exam. Visit official Website CISCE for detail information about ISC Board Class-11 Physics.

Numerical on Distance Displacement Velocity Acceleration Graph Class 11 Physics ISC Nootan Solutions Ch-4 Motion in a Straight Line
| Board | ISC |
| Class | 11 |
| Subject | Physics |
| Book | Nootan |
| Chapter-4 | Motion in a Straight Line. |
| Topics | Numerical on Distance Displacement Velocity Acceleration Graph |
| Academic Session | 2024-2025 |
Numerical on Distance Displacement Velocity Acceleration Graph
( Class 11 Physics ISC Nootan Solutions Ch-4 Motion in a Straight Line )
Que-1: In the given fig., the time-displacement graph of a moving body is given. Draw its time-velocity graph and state :
(i) When was the body going faster? (ii) How much total distance the body has travelled? (iii) What is total displacement in the position of the body ? (iv) What was the acceleration of the body from the beginning upto A?
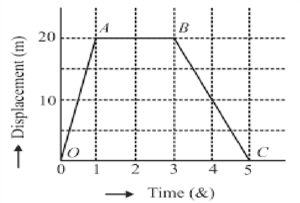
Sol: (i) between 0 to 1 sec.
(ii) distance = speed x time
= 20 x 2 = 40 m. Ans.
(iii) Total displacement in the position of a body is zero.
(iv) The acceleration is zero. 
Que-2: In the adjoining figure is shown the time-distance (t-s) graph of a cyclist. Find out from the graph : (i) maximum speed of the cyclist , (ii) average speed in the whole journey .
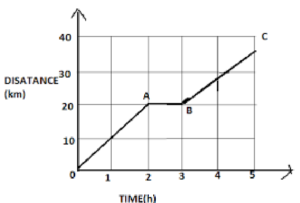
Sol: (i) Maximum speed =distance/time
= 20km/2h = 10km/h Ans.
(ii) Average speed = total distance/total time
= 35km/5h =7km/h Ans.
Que-3: A car moves first for 0.1 hour with a velocity of 20km/h, then for 0.4 hour with a velocity of 60km/h and in the last for 0.2 hour with a velocity of 20km/h. Draw time-velocity graph for the car and use it to find :
(i) How much distance the car moves in the first time-interval. (ii) How much distance the car moves in the whole journey. (iii) How much time the car take in first 14km. Indicate that area in your graph which indicates the journey of first 14km.
Sol: Given: For t₁ = 0.1 hr, the velocity of the car, v₁ = 20 km/hr
For t₂ = 0.4 hr , the velocity of car, v₂ = 60 km/hr
For t₃ = 0.2 hr, the velocity of car, v₃ = 20 km/hr
We are required to find the distance, time, and area covered by the car by using the graph inserted.
We know the area of the velocity-time graph gives the distance travelled.
i) For the distance travelled in the first interval(0-0.1 hr),
From the graph, find the area of the A1 section which is in a rectangle shape so the area is length × breadth
Area of A1 section = length × breadth
= 0.1×20
= 2 km Therefore, The total distance travelled in the first interval by car is 2 km.
ii) For the distance travelled in the whole journey(0-0.7 hr),
From the graph, find the area of the A1, A2, and A3 sections which is in a rectangle shape so the area is length × breadth
Area of A1 section = length × breadth
= 0.1×20
= 2 km
Area of A2 section = length × breadth
= (0.5-0.1)×60
= 0.4×60
= 24 km
Area of A3 section = length × breadth
= (07-0.5)×20
= 0.2×20
= 4 km
Total distance = total area(A1+A2+A3)
= 2+24+4
= 30 km Therefore, The total distance travelled by car in the whole journey is 30km.
(iii) The car travels 2 km in 0.1 hr at the first interval then the remaining distance is (14-2) = 12 km
t₁ = 0.1hr
We know, time = distance/ velocity ——(1)
Here the car travels the next 24 km at 60 km/hr so for the distance of 12 km the car travelled at 60km/hr
On applying v = 60 km/hr and d = 12 km in equation(1)
t₂ = 12/60
= 0.2 hr
Total time (t) = t₁+t₂
= 0.1+0.2
= 0.3 hr Therefore, The time taken by the car in the first 14 km is 0.3 hours.
Que-4: A body starts from rest in a straight line with an acceleration of 8.0 m/s^2. Draw its time-velocity graph and determine :
(i) Velocity of the body after 5 seconds.
(ii) How much distance the body has moved in first 5 seconds ? (iii) What average velocity of the body is during this time ?
Sol: a = 8 m/s^2
i) u = 0 ; t = 5 s
As v = u + a t
so, v = 0+ 8×5 = 40 m/s Ans.
ii) Also, s = u t + 1/2 a t^2
so, s = 0 + 1/2×8×5^2 = 100 m Ans.
iii) average velocity = (u + v)/2
= (0+40)/2
=20m/s Ans.
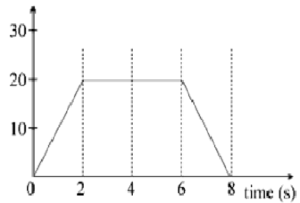
Que-5: How far does the runner whose time-velocity graph is shown in the figure travel in 16 seconds ? What is the acceleration of the runner at t = 11 second?
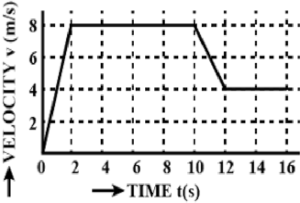
Sol: The total distance covered can be obtained by calculating area under the v – t graph between t = 0 to t = 16 s
Now, The whole figure can be divided into 3 figures
A1 → a triangle from origin to t = 1s
A2 → a trapezium from t =1 s to t = 12 s above v = 4 m/s
A3 → a rectangle from t = 1 s to t = 16 s below v = 4 m/s
A1 = ½ x 1 x 4 = 2 m
A2 = ½ x ([12 – 1] + [10 – 2]) x (8 – 4)
= ½ x 19 x 4 = 38 m
A3 = (16 – 1) x 4
= 60 m
Hence, The total distance covered = A1 + A2 + A3
= 2 + 38 + 60
= 100 m Ans.
(ⅱ) acceleration at 11 sec
= acceleration between 10-12 sec
= v/t = (4-8)/(12-10) = -2m/s^2 Ans.
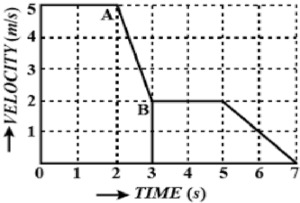
Que-6: The time-velocity graph of a car is shown in the figure. Calculate :
(i) acceleration from A to B, (ii) distance travelled in the last 4 seconds.
Sol: (i) Given : u=5, v=2, t=1
a=v-u/t
=2-5/1
=-3m/s^2 Ans.
(ii) distance travelled in the last 4 seconds
= area under the graph
= 2×2+1/2×2×2
= 4+2
= 6m Ans.
Que-7: The figure shows the time-distance (t-s) graphs of two cars which start simultaneously in the same direction. Calculate from the graph :
(i) By how much distance the car A was ahead of car B initially. (ii) Which car is moving faster? What their speed are? (iii) After how much time and at which place the car B will catch the car A.
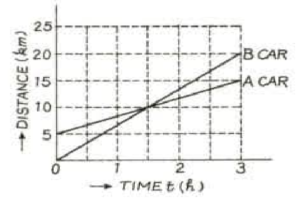
Sol: (i) As show in figure car A is 5km ahead of car B.
(II) Car B is moving faster as it has greater slope.
(iii) Catching time will be when two lines cross each other i.e., 5km
again distance from starting point = 10km as shown in figure.
Que-8: As soon as a car just starts from rest in a certain direction, a scooter moving with a uniform speed overtakes the car. Their time-speed (t-v) graphs are shown in the above figure. Calculate from the graph :
(i) acceleration of a car initially, (ii) the time at which the speed of the car becomes equal to the speed of the scooter, (iii) the difference in the distances traversed by the scooter and the car in 12 seconds, (iv) after how much time this difference will become 120 metres.

Sol: (i) acceleration of car =
a = v/t = (60-0)/(12-0)
= 60/12 = 5 m/s^2. Ans.
(ii) Speed of both car will be equal at crossing of lines i.e., 6 sec in between 4 and 8 sec.
(iii) Distance travelled by car = 1/2x12x60 = 360m
= distance travelled by scooter = 12×30 = 360m
= difference = 360-360 = 0m. Ans.
(iv) Let after Y sec difference becomes 120m
then 1/2x12x60 + (Y-12)x60 – Yx30 = 120
= 360 + 60Y – 720 – 30Y = 120
Y = 16 sec. Ans.
Que-9: The figure shows the time-velocity graph for a body thrown vertically up. Calculate from the graph :
(i) the type of motion, (ii) the initial velocity and acceleration, (iii) maximum height attained by the body, (iv) after how much time the body will return.
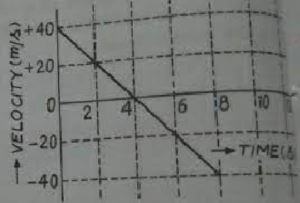
Sol: (i) Uniformly retarded upward motion for the first four seconds, then uniformly accelerated downwards motion.
(ii) initial velocity is 40 m/s and initial acceleration is 10 m/s^2
(iii) Maximum height attained by a body is 80m
(iv) The body will return in 8 second.
Que-10: The figure (a) below shows the time-acceleration graph of a body. Draw the corresponding time-velocity graph. At time t = 0, the velocity v = 0.
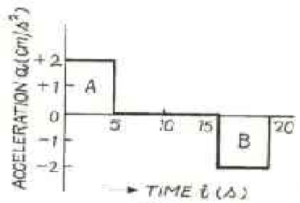
Sol: Time-velocity graph.
Que-11: A car accelerates uniformly on a straight road from rest to a speed of 180 km/h in 25s. Find the distance covered by the car in this time-interval
Sol: As per the theory of Kinematics,
Vf = Vi + at → (1)
Where initial velocity Vi = 0 km/hour, as car starts from rest.
Final velocity, Vf = 180 Km/hour = 180 x 1000/ 3600 = 50 m/s
t = 25 seconds
So acceleration, a = (Vf-Vi)/t = (50-0)/25 = 2 m/s^2
Now let’s find the distance covered by the car.
Distance, d = Vit + 1/2 at^2
= (0x25) + 1/2 (2)(252) = 625 meter Ans.
Que-12: A body travels a distance of 20 m in the 7th second and 24 m in 9th second. How much distance shall it travel in the 15th second?
Sol: let u is initial velocity and a is acceleration
⇒S=u+1/2a(2n-1) 2
⇒ 20 = u + 1/2a(14-1) = u + 13a/2
→ 2u + 13a = 40 ……(i)
2u = u + 1/2a(18-1)
2u+17a = 48 …..(ii)
Subtracting equation (i) from (ii) we get
4a = 8 ⇒ a = 2 m/s²
From equation (i)
2u+13 x 2 = 40
2u-40-26 = 14
⇒ u = 7m/s
S15 = u + 1/2a(2×15-1)
= 7+1/2×2(29)
= 7 +29=36 m Ans.
Que-13: A particle experiences constant acceleration for 20 second after starting from rest. If it travels a distance S₁ in the first 10 seconds and distance S₂ in the next 10 seconds, then find the relation between S₁ and S₂.
Sol: – t₁ = 10s
t₂ = 20s
S₁ = 1/2at² = 1/2a (10)²
S₁ = 50a
S₂ = 1/2a (20)² – 1/2a (10)²
= 200a – 50a
S₂ = 150a
S₂ = 3S₁ Ans.
— : end of Numerical on Distance Displacement Velocity Acceleration Graph Class 11 Physics Solutions :–
Return to : – Nootan Solutions for ISC Class-11 Physics
Thanks
Please Share with your friends if helpful



there are only few solution according to new book for year 2026
we are updating one by one chapter as 2025-26 syllabus